- 318.50 KB
- 2021-06-23 发布
23.3.3 相似三角形的判定
【学习目标】
1、两个三角形相似的判定方法2:如果一个三角形的两条边与另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似。
2、两个三角形相似的判定方法3:如果一个三角形的三条边和另一个三角形的三条边对应成比例,那么这两个三角形相似.
【学习重难点】
相似三角形的判定定理2和3
【学习过程】
一、课前准备
判断两个三角形相似有哪几种方法?
有两种方法(1) ,(2) 。
二、学习新知
自主学习:
1、观察课本67页图23-3-10,完成填空。
然后通过量角或量线段计算之后,得出△ADE∽△ABC。
分析题目条件:(1)有一个公共角∠A,(2)AD=AB, AE=AC,
结论:△ADE∽△ABC
探 索: 如果一个三角形的两条边与另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似吗?
2、总结另一个判断相似的方法:如果一个三角形的两条边与另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似.
符号语言:
∵,
∴△ABC ∽△.
3、探 索:如果两个三角形的三条边对应成比例,那么这两个三角形相似吗?完成下面的做一做,再讨论总结判断另一个相似的方法。
4、课本69页做一做
我们可以发现这两个三角形相似.即:
3
如果一个三角形的三条边和另一个三角形的三条边对应成比例,那么这两个三角形相似.
实例分析:
例1、例3 判断图中△AEB和△FEC是否相似?
证明:
例4、在△ABC和△A′B′C′中,已知:AB=6 cm, BC=8 cm,AC=10 cm,A′B′=18 cm,B′C′=24 cm, A′C′=30 cm.试判定△ABC与△A′B′C′是否相似,并说明理由.(小组讨论完成)
证明:
【随堂练习】
1、在△ABC和△中,∠C=∠=90°,AC=12,BC=15,=8,则当
=____________时,△ABC∽△.
2、在△ABC中,AB:BC:CA=2:3:4,在△A1B1C1中,A1B1=1,C1A1=2,当B1C1=______时,△ABC∽△A1B1C1。
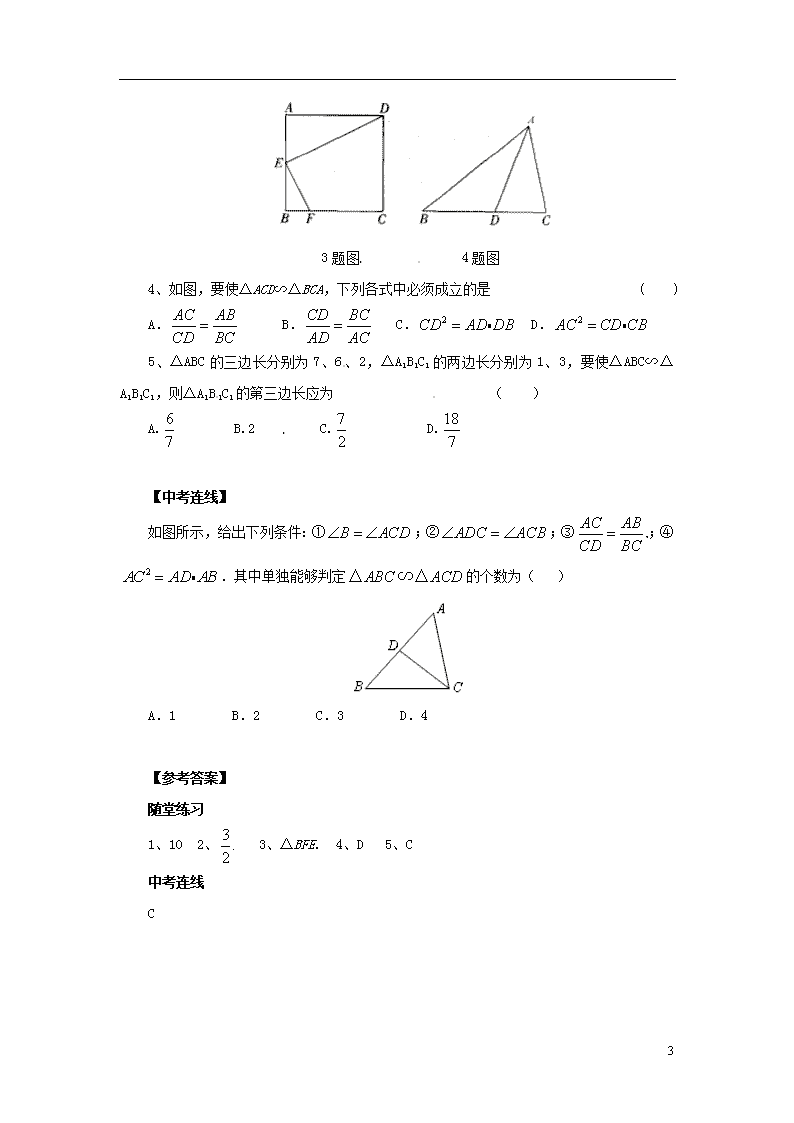
3、如图,在正方形ABCD中,E为AB的中点,BF=BC,则与△AED相似的三角形是_______.
3
3题图 4题图
4、如图,要使△ACD∽△BCA,下列各式中必须成立的是 ( )
A. B. C. D.
5、△ABC的三边长分别为7、6、2,△A1B1C1的两边长分别为1、3,要使△ABC∽△A1B1C1,则△A1B1C1的第三边长应为 ( )
A. B.2 C. D.
【中考连线】
如图所示,给出下列条件:①;②;③;④.其中单独能够判定的个数为( )
A.1 B.2 C.3 D.4
【参考答案】
随堂练习
1、10 2、 3、△BFE. 4、D 5、C
中考连线
C
3
您可能关注的文档
相关文档
- 2019九年级数学上册 第23章 图形的2021-06-23 19:44:173页
- 高考数学专题复习练习选修4-1 第12021-06-19 15:51:055页
- 高中数学人教a版选修4-1同步辅导与2021-06-04 03:20:4235页
- 相似三角形的判定12021-05-28 22:00:0010页
- 九年级下册数学人教版课件27-2-1 2021-05-28 20:00:1925页
- 华师版九年级上册数学同步练习课件2021-05-28 19:41:1415页
- 数学冀教版九年级上册课件25-4 相2021-05-28 17:49:4614页
- 华师版数学九年级上册课件-第23章-2021-05-28 12:55:0618页
- 九年级下册数学人教版课件27-2-1 2021-05-28 10:11:3531页
- 【数学】2020届一轮复习人教A版 2021-05-27 21:30:5415页