华师版数学九年级上册课件-第23章-23相似三角形的判定 18页

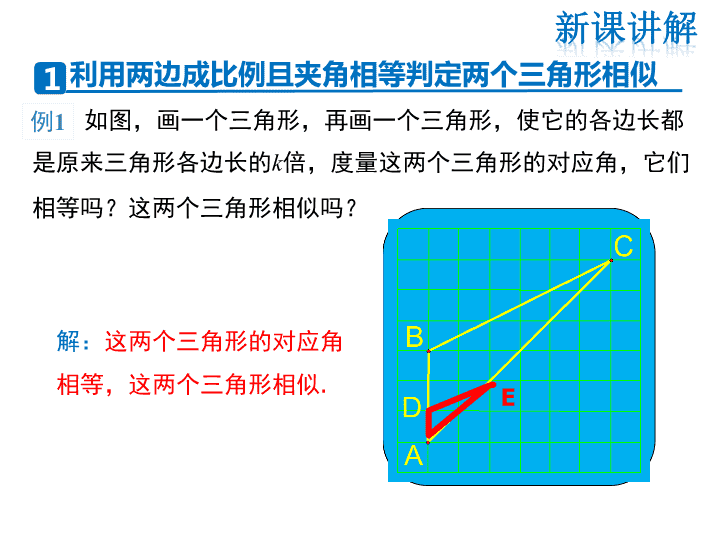
HS九(上) 教学课件 第23章 图形的相似 23.3.2 相似三角形的判定 第2课时 利用两边和一夹角、三边判定 两个三角形相似 问题1 ：两个三角形全等有哪些判定方法？ 问题2： 我们学习过哪些判定三角形相似的方法？ 如图，画一个三角形，再画一个三角形，使它的各边长都 是原来三角形各边长的k倍，度量这两个三角形的对应角，它们 相等吗？这两个三角形相似吗？ D C B A E 解：这两个三角形的对应角 相等，这两个三角形相似. 1 利用两边成比例且夹角相等判定两个三角形相似 例1 如图，在△ABC和△A′B′C′中,∠A＝∠A′ , A′B′:AB=A′C′:AC.求证:△ABC∽△A′B′C′. A′ B′` C′ A B C ED 证明:在△ABC的边AB、AC(或它们的延长线) 上分别截取AD=A′B′,AE=A′C′,连结DE. ∠A=∠A′, 这样,△ADE≌△A′B′C′. ∵A′B′:AB=A′C′:AC， ∴ AD:AB=AE:AC， ∴DE∥BC， ∴△ADE∽△ABC， ∴△A′B′C′∽△ABC. 例2 如果一个三角形的两边长与另一个三角形的两边长对应成 比例，并且夹角相等，那么这两个三角形相似 . (两边成比例且夹角相等的两个三角形 相似) A B C A′ B′ C′ ∵A′B′:AB=A′C′:AC,∠A=∠A′ ， ∴△A′B′C′∽△ABC. 问题：如果两个三角形两边成比例，但对应相等的角不 是两条对应边的夹角，那么两个三角形是否相似呢？画 一画，量一量. A B C D E F 不相似 如果两个三角形两边对应成比例，但对应相等的角不 是两条对应边的夹角，那么两个三角形不一定相似. 注意：对应相等的角一定要是两条对应边的夹角. 1.如图，△ABC与△ADE都是等腰三角形，AD=AE，AB=AC， ∠DAB=∠CAE.求证：△ABC∽△ADE.                   AD AE,AB AC, AD AE .AB AC DAB CAE, DAB BAE CAE BAE, DAE BAC,即 △ABC∽△ADE. 练一练： 证明： 4.5 5 5 4 ,4 25,5 25.4 AC BC AD AC AC ADAD AD          ， △ABC∽△DCA， 16, 4, 5, 7 2 6 4 4,1 5 57 2 . AB BC AC CD AB BC CD AC AB BC CD AC B ACD                 ， 解： ， 又 ， 2.已知：如图，在四边形ABCD中，∠B=∠ACD，AB=6，BC=4， AC=5，CD= ，求AD的长．  A B C D 证明:在△ABC的边AB(或延长线)上截取AD=A′B′, A′ B′ C′ A B C D E 过点D作DE∥BC交AC于点E. 又A′B′:AB=B′C′:BC=C′A′:CA, ∴AD:AB=AE:AC. ∵∠A=∠A′，∴△ADE∽△ABC. AD=A′B′,∴AD:AB=A′B′:AB， ∴DE:BC=B′C′:BC, EA:CA=C′A′:CA. 因此DE=B′C′, EA=C′A′. ∴△A′B′C′∽△ABC. ∴△ADE≌△A′B′C′, △ABC∽△A′B′C′ 如果一个三角形的三条边和另一个三角形的三条边 对应成比例,那么这两个三角形相似. 简单地说：三边成比例的两个三角形相似. A B C C′B′ A′ AC C'A' BC C'B' AB B'A'  1.如图,已知 ，证明∠BAD=∠CAE. A D C E B 证明：∵ ∴△ABC∽△ADE， ∴∠BAC=∠DAE， ∴∠BAC－∠DAC=∠DAE－∠DAC， 即∠BAD=∠CAE. AE AC DE BC AD AB  AB BC AC AD DE AE   ， 练一练： 2.已知AB=10，BC=8 ，AC=16，A′B′=16，B′C′=12.8， C′A′=25.6，证明△ABC∽△A′B′C′. 10 5 16 8   AB A B′ ，′ 16 5 25.6 8  ' AC AC ，′ 8 5 12.8 8  ' BC B C ，′ ∴△ABC∽△A′B′C′. 证明： ★判定三角形相似的方法之一： 如果题中给出了两个三角形的三边的长，分别算出三 条对应边的比值，看是否相等，计算时最长边与最长边对 应，最短边与最短边对应. 1.根据下列条件，判断△ABC与△A´B´C´是否相似， 并说明理由： （1）∠A=120°，AB=3cm，AC=6cm,∠A´=120°， A´B´=6cm，A´C´=12cm. ∴A′B′:AB=A′C′:AC,∠A=∠A′ ， ∴△A′B′C′∽△ABC. 解：（1）∵A′B′: AB=2 , A′C′: AC=2, ∠A=∠A′=120°. (2) AB=4cm ，BC =6cm ，AC =8cm,A´B´=12cm ， B´C´=18cm ，A´C´=21cm 4 1 12 3 6 1 18 3 8 21 AB A B BC B C AC A C AB BC AC A B B C A C                 （2） ， ， ， 解： ， ∴△ABC与△A′B′C′的对应边不成比例，它们不相似. 2.判断图中△AEB 和△FEC是否相似？ 解：∵ ∴△AEB∽△FEC. ∵∠AEB＝∠CEF， 54 30 36 45 E A F C B ， 2 3 36 54  FE AE ， 2 3 30 45  CE BE .AE BE FE CE ∴ 相似三角形的判定定理3： 三条边成比例的两个三角形相似. ★相似三角形的判定定理： 相似三角形的判定定理1：两角分别相等的两个三角形相似. 相似三角形的判定定理2： 两边成比例且夹角相等的两个三角 形相似. 注意：对应相等的角一定要是两条对应边的夹角.