- 4.33 MB
- 2021-05-25 发布
24.5 画相似图形
学前温故
我们把形状相同的两个多边形叫做________,其对应边的比叫做______.
新课早知
1.位似图形的有关概念
如果两个多边形相似,而且____相交于一点,像这样的相似叫做位似,这一点叫做____.这时的相似比又叫做____.
2.下列命题正确的是( ).
A.全等图形一定是位似图形
B.相似图形一定是位似图形
C.位似图形一定是全等图形
D.位似图形是具有某种特殊位置的相似图形
3.下列说法正确的是( ).
A.两个位似图形对应点连线有可能无交点
B.两个位似图形对应点连线的交点个数为1或2
C.两个位似图形对应点连线的交点有且只有一个
D.两个位似图形对应点连线的交点个数不少1
4.位似图形上任意一对对应点到位似中心的距离之比等于______.利用位似变换放大或缩小图形.
5.如图,五边形ABCDE和五边形A1B1C1D1E1是位似图形,且PA1=PA,则AB∶A1B1等于( ).
A. B. C. D.
答案:快乐预习·感知
学前温故
相似多边形 相似比
新课早知
1.对应顶点的连线 位似中心
位似比
2.D 3.C 4.位似比 5.B
画位似图形
【例题】 已知等边△ABC,画一个与之相似且它们的相似比为2的△A′B′C′.
解:如图1,当设位似中心在△ABC的内部时,取内心O作为位似中心.
(1)在AO、BO、CO上分别取中点A′、B′、C′,连结A′B′、B′C′、A′C′,则△ABC∽△A′B′C′,且有A′B′∶AB=1∶2.
3
图1
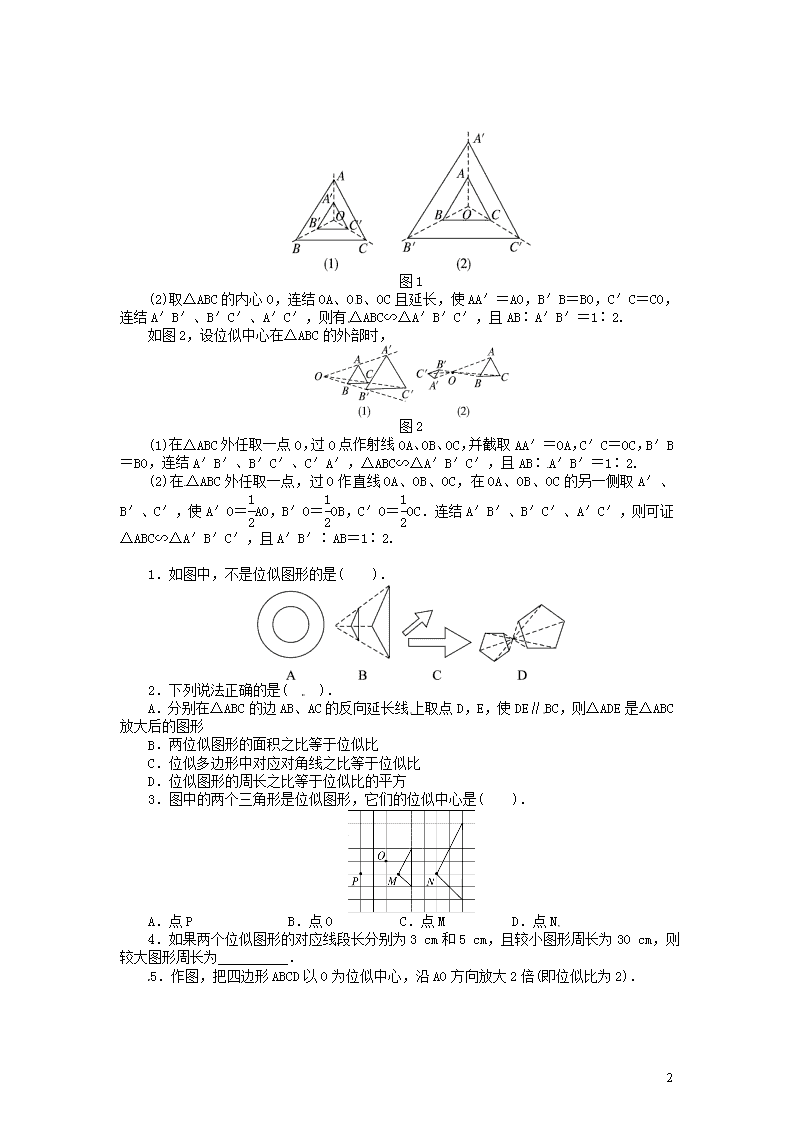
(2)取△ABC的内心O,连结OA、OB、OC且延长,使AA′=AO,B′B=BO,C′C=CO,连结A′B′、B′C′、A′C′,则有△ABC∽△A′B′C′,且AB∶A′B′=1∶2.
如图2,设位似中心在△ABC的外部时,
图2
(1)在△ABC外任取一点O,过O点作射线OA、OB、OC,并截取AA′=OA,C′C=OC,B′B=BO,连结A′B′、B′C′、C′A′,△ABC∽△A′B′C′,且AB∶A′B′=1∶2.
(2)在△ABC外任取一点,过O作直线OA、OB、OC,在OA、OB、OC的另一侧取A′、B′、C′,使A′O=AO,B′O=OB,C′O=OC.连结A′B′、B′C′、A′C′,则可证△ABC∽△A′B′C′,且A′B′∶AB=1∶2.
1.如图中,不是位似图形的是( ).
2.下列说法正确的是( ).
A.分别在△ABC的边AB、AC的反向延长线上取点D,E,使DE∥BC,则△ADE是△ABC放大后的图形
B.两位似图形的面积之比等于位似比
C.位似多边形中对应对角线之比等于位似比
D.位似图形的周长之比等于位似比的平方
3.图中的两个三角形是位似图形,它们的位似中心是( ).
A.点P B.点O C.点M D.点N
4.如果两个位似图形的对应线段长分别为3 cm和5 cm,且较小图形周长为30 cm,则较大图形周长为__________.
5.作图,把四边形ABCD以O为位似中心,沿AO方向放大2倍(即位似比为2).
3
答案:1.C 2.C
3.A 位似图形的对应顶点的连线交于一点,这一点就是位似中心,通过图形可以观察出点P是位似中心.
4.50 cm
5.解:放大图形
作法:(1)连结OA,并延长AO到A′,使OA′=2OA,如图.
(2)连结OB、OC、OD,并延长BO到B′,延长CO到C′,延长DO到D′,使OB′=2OB,OC′=2OC,OD′=2OD.
(3)连结A′B′、B′C′、C′D′、D′A′,则四边形A′B′C′D′与四边形ABCD关于O点成位似图形,并且位似比为2.
3
相关文档
- 九年级数学上册第四章图形的相似42021-05-24 18:08:453页
- 博海名师知识点总结北师大中考知识2021-05-24 14:22:484页
- 图形的相似数学教案2021-05-24 12:47:112页
- 北师大版数学九年级上册同步练习课2021-05-24 12:26:5411页
- 九年级数学上册第四章图形的相似12021-05-24 12:00:1213页
- 华师版九年级上册数学同步练习课件2021-05-23 00:44:3110页
- 北师大版数学九年级上册同步练习课2021-05-22 21:06:3617页
- 九年级数学上册第23章图形的相似232021-05-22 19:35:063页
- 九年级数学上册第四章图形的相似专2021-05-22 16:09:4721页
- 九年级数学上册第23章图形的相似232021-05-22 12:43:053页