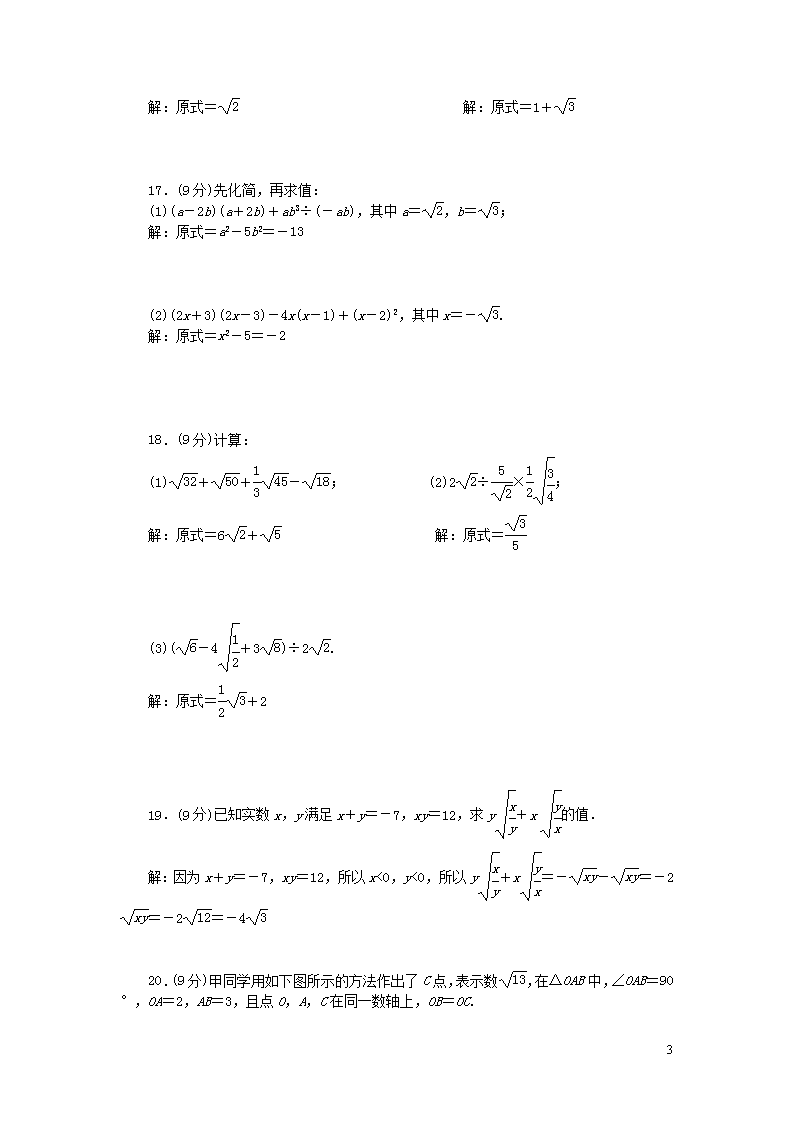- 154.00 KB
- 2021-05-25 发布
第二章检测题
(时间:100分钟 满分:120分)
一、选择题(每小题3分,共30分)
1.(2019·天门)下列各数中,是无理数的是(D)
A.3.1415 B. C. D.
2.(2019·绵阳)若=2,则a的值为(B)
A.-4 B.4 C.-2 D.
3.(2019·云南)要使有意义,则x的取值范围为(B)
A.x≤0 B.x≥-1 C.x≥0 D.x≤-1
4.(2019·益阳)下列运算正确的是(D)
A.=-2 B.(2)2=6 C.+= D.×=
5.(2019·河南)下列计算正确的是(D)
A.2a+3a=6a B.(-3a)2=6a2 C.(x-y)2=x2-y2 D.3-=2
6.实数a,b在数轴上的位置如图所示,且|a|>|b|,则化简-|a+b|的结果为( C )
A.2a+b B.-2a+b C.b D.2a-b
7.下列说法:①5是25的算术平方根;②是的一个平方根;③(-4)2的平方根是-4;④立方根和算术平方根都等于自身的数是0和1.其中正确的个数有( C )
A.1个 B.2个 C.3个 D.4个
8.(2019·南通)小明学了在数轴上画出表示无理数的点的方法后,进行练习:首先画数轴,原点为O,在数轴上找到表示数2的点A,然后过点A作AB⊥OA,使AB=3(如图).以O为圆心,OB长为半径作弧,交数轴正半轴于点P,则点P所表示的数介于(C)
A.1和2之间
B.2和3之间
C.3和4之间
D.4和5之间
9.(泸州中考)已知三角形的三边长分别为a,b,c,求其面积问题,中外数学家曾经进行过深入研究,古希腊的几何学家海伦(Heron,约公元50年)给出求其面积的海伦公式S=,其中p=;我国南宋时期数学家秦九韶(约1202-1261)曾提出利用三角形的三边求其面积的秦九韶公式S=,若一个三角形的三边长分别为2,3,4,则其面积是( B )
5
A. B. C. D.
10.(2019·随州)“分母有理化”是我们常用的一种化简的方法,如:==7+4,除此之外,我们也可以用平方之后再开方的方式来化简一些有特点的无理数,如:对于-,设x=-,易知>,故x>0,由x2=(-)2=3++3--2=2,解得x=,即-=.根据以上方法,化简+-后的结果为(D)
A.5+3 B.5+ C.5- D.5-3
二、填空题(每小题3分,共15分)
11.(2019·河南)计算:-2-1=1.
12.(2019·宁波)请写出一个小于4的无理数:.
13.(2019·滨州)计算:(-)-2-|-2|+÷=2+4.
14.(2019·青海)根据如图所示的程序,计算y的值,若输入x的值是1时,则输出的y值等于-2.
15.(2019·枣庄)观察下列各式:
=1+=1+(1-),=1+=1+(-),
=1+=1+(-),…
请利用你发现的规律,计算:
+++…+,其结果为2018.
三、解答题(共75分)
16.(8分)计算:
(1)(2019·十堰)(-1)3+|1-|+; (2)1+()-1-÷()0.
解:原式= 解:原式=1+
17.(9分)先化简,再求值:
(1)(a-2b)(a+2b)+ab3÷(-ab),其中a=,b=;
5
解:原式=a2-5b2=-13
(2)(2x+3)(2x-3)-4x(x-1)+(x-2)2,其中x=-.
解:原式=x2-5=-2
18.(9分)计算:
(1)++-; (2)2÷×;
解:原式=6+ 解:原式=
(3)(-4+3)÷2.
解:原式=+2
19.(9分)已知实数x,y满足x+y=-7,xy=12,求y+x的值.
解:因为x+y=-7,xy=12,所以x<0,y<0,所以y+x=--=-2=-2=-4
20.(9分)甲同学用如下图所示的方法作出了C点,表示数,在△OAB中,∠OAB=90°,OA=2,AB=3,且点O,A,C在同一数轴上,OB=OC.
(1)请说明甲同学这样做的理由;
(2)仿照甲同学的做法,在如下所给数轴上描出表示-的点F.
5
解:(1)在Rt△OAB中,由勾股定理得OB2=OA2+AB2,所以OC=OB===, 即点C表示数
(2)画图略.在△ODE中,∠EDO=90°,OD=5,DE=2,则OF=OE=,即F点为-
21.(10分)如果正方形网格中的每一个小正方形的边长都是1,则每个小格的顶点叫做格点.
(1)如图①,以格点为顶点的△ABC中,请判断AB,BC,AC三边的长度是有理数还是无理数?
(2)在图②中,以格点为顶点画一个三角形,使三角形的三边长分别为3,,2.
解:(1)AB=4,AC==3,BC==,所以AB的长度是有理数,AC和BC的长度是无理数
(2)图略
22.(10分)小丽想用一块面积为400 cm2的正方形纸片沿着边的方向剪出一块面积为300 cm2的长方形,并使长方形纸片的长宽之比为3∶2,请问小丽能否剪出符合要求的长方形纸片,请说明理由.
解:小丽不能剪出符合要求的长方形纸片.理由为:设长方形纸片的长为3x cm,宽为2x cm,由题意则有:3x·2x=300,6x2=300,x2=50,所以x=,所以长方形纸片的长为3x=3,又因为>=7,所以3x=3>21(cm),而原正方形纸片的边长为20 cm,故小丽不能剪出符合要求的长方形纸片
23.(11分)阅读下列材料,然后解答下列问题:
在进行代数式化简时,我们有时会碰上如,这样的式子,其实我们还可以将其进一步化简:
(一)==;
(二)===-1;
(三)====-1.
以上这种化简的方法叫分母有理化.
(1)请用不同的方法化简:
5
①参照(二)式化简;
②参照(三)式化简;
(2)化简:+++…+.
解:(1)①原式===-
②原式====-
(2)原式=+++…+==
5
相关文档
- 全国各地中考数学试卷试题分类汇编2021-05-25 00:04:2217页
- 人教版七年级数学下册第六章《实数2021-05-24 23:54:266页
- 中考首轮总复习系列训练优化组合数2021-05-24 22:33:112页
- 八年级数学上册第二章实数4估算作2021-05-24 21:34:4214页
- 中考数学总复习教案课时1实数的有2021-05-24 21:05:164页
- 八年级数学上册第二章实数2-7二次2021-05-24 19:29:5125页
- 2020秋八年级数学上册第二章实数微2021-05-24 19:25:4314页
- 八年级数学上册第3章实数3-2立方根2021-05-24 16:41:1424页
- 八年级上数学课件《实数》 (6)_苏2021-05-24 15:24:3015页
- 2019版七年级数学下册第六章实数6-2021-05-24 15:06:1236页