中考数学一轮精品学案：函数及其图象1 3页

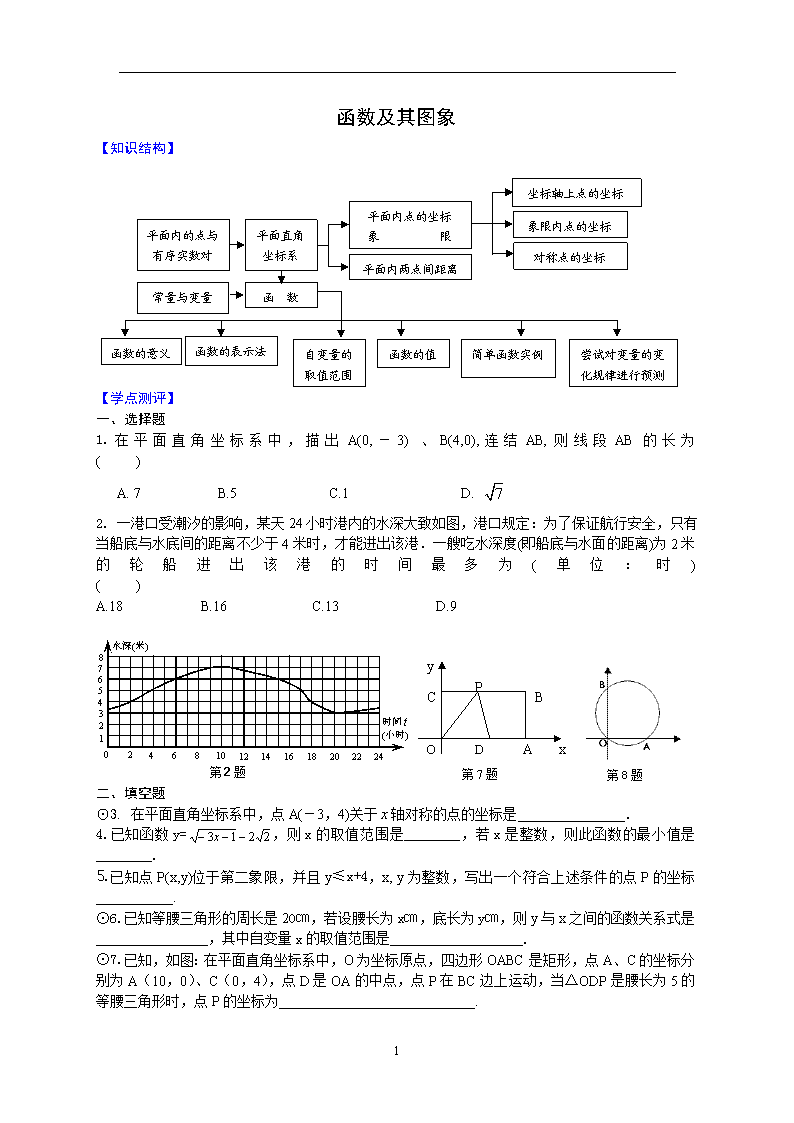
‎ ‎ 函数及其图象 ‎【知识结构】‎ 函数的意义 平面内的点与有序实数对 平面直角坐标系 平面内点的坐标 象 限 平面内两点间距离 坐标轴上点的坐标 象限内点的坐标 对称点的坐标 常量与变量 函 数 函数的表示法 自变量的 取值范围 函数的值 简单函数实例 尝试对变量的变化规律进行预测 ‎【学点测评】‎ 一、选择题 ‎1.在平面直角坐标系中，描出A(0,－3) 、B(4,0),连结AB,则线段AB的长为 ( )‎ ‎ A. 7 B.5 C.1 D. ‎ ‎2. 一港口受潮汐的影响，某天24小时港内的水深大致如图，港口规定：为了保证航行安全，只有当船底与水底间的距离不少于4米时，才能进出该港．一艘吃水深度(即船底与水面的距离)为2米的轮船进出该港的时间最多为(单位：时) ( )‎ A.18 B.16 C.13 D.9‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎88‎ ‎0‎ ‎2‎ ‎4‎ ‎6‎ ‎8‎ ‎10‎ ‎12‎ ‎14‎ ‎16‎ ‎18‎ ‎20‎ ‎22‎ ‎24‎ 时间t ‎(小时)‎ 水深(米)‎ 第２题 第8题 C A P O B D y x 第7题 二、填空题 ‎⊙3. 在平面直角坐标系中，点A(－3，4)关于轴对称的点的坐标是 ．‎ ‎4.已知函数y=，则x的取值范围是________，若x是整数，则此函数的最小值是________.‎ ‎⒌已知点P(x,y)位于第二象限，并且y≤x+4，x, y为整数，写出一个符合上述条件的点P的坐标___________.‎ ‎⊙6.已知等腰三角形的周长是20㎝，若设腰长为x㎝，底长为y㎝，则y与x之间的函数关系式是________________，其中自变量x的取值范围是___________________.‎ ‎⊙7.已知，如图：在平面直角坐标系中，O为坐标原点，四边形OABC是矩形，点A、C的坐标分别为A（10，0）、C（0，4），点D是OA的中点，点P在BC边上运动，当△ODP是腰长为5的等腰三角形时，点P的坐标为____________________________.‎ 3‎ ‎ ‎ ‎8如图，一个圆经过原点O，与轴和轴分别交于点A(，0)、B（0，2），作此圆的内接△OAM并使的△OAM的面积最大，则点M的坐标为 ．‎ 三、解答题 ‎⒐先将一矩形ABCD置于直角坐标系中，使点A与坐标系中原点重合，边AB．AD分别落在x轴、y轴上（如图1），再将此矩形在坐标平面内按逆时针方向绕原点旋转30°（如图2），若AB=4，BC=3，求图1和图2中点B的坐标，点C的坐标．‎ ‎【疑点难点】‎ ‎10.小明早晨从家里出发匀速步行去上学，小明的妈妈在小明出发后10分钟，发现小明的数学课本没带，于是她带上课本立即匀速骑车按小明上学的路线追赶小明，结果与小明同时到达学校．已知小明在整个上学途中，他出发后分钟时，他所在的位置与家的距离为千米，且与之间的函数关系的图像如图中的折线段OA－AB所示．‎ ‎⑴试求折线段OA－AB所对应的函数关系式；‎ ‎⑵请解释图中线段AB的实际意义；‎ ‎1‎ A B ‎20‎ ‎12‎ t(分钟)‎ s(千米)‎ O ‎⑶请在所给的图中画出小明的妈妈在追赶小明的过程中，她所在位置与家的距离（千米）与小明出发后的时间（分钟）之间函数关系的图像． ‎ ‎ ‎ ‎ ‎ ‎【探索创新】‎ ‎11.如图12－①，平面直角坐标系xOy中有点B（2，3）和C（5，4），求△OBC的面积.‎ 解：过点B作BD⊥x轴于D，过点C作CE⊥x轴于E.依题意,可得S△OBC = S梯形BDEC + S△OBD－ S△OCE ==×(3+4)×(5－2)+×2×3－×5×4=3.5.∴△OBC的面积为3.5.‎ ‎⑴如图12－②，若B（x1，y1）、C（x2，y2）均为第一象限的点，O、B．C三点不在同一条直线上. 仿照例题的解法,求△OBC的面积（用含x⒈x⒉y⒈y2的代数式表示）；‎ ⑵ 如图12－③，若三个点的坐标分别为A（2,5），B（7,7），C（9,1），求四边形OABC的面积.‎ 3‎ ‎ ‎ 3‎