中考数学压轴题专题训练 20页

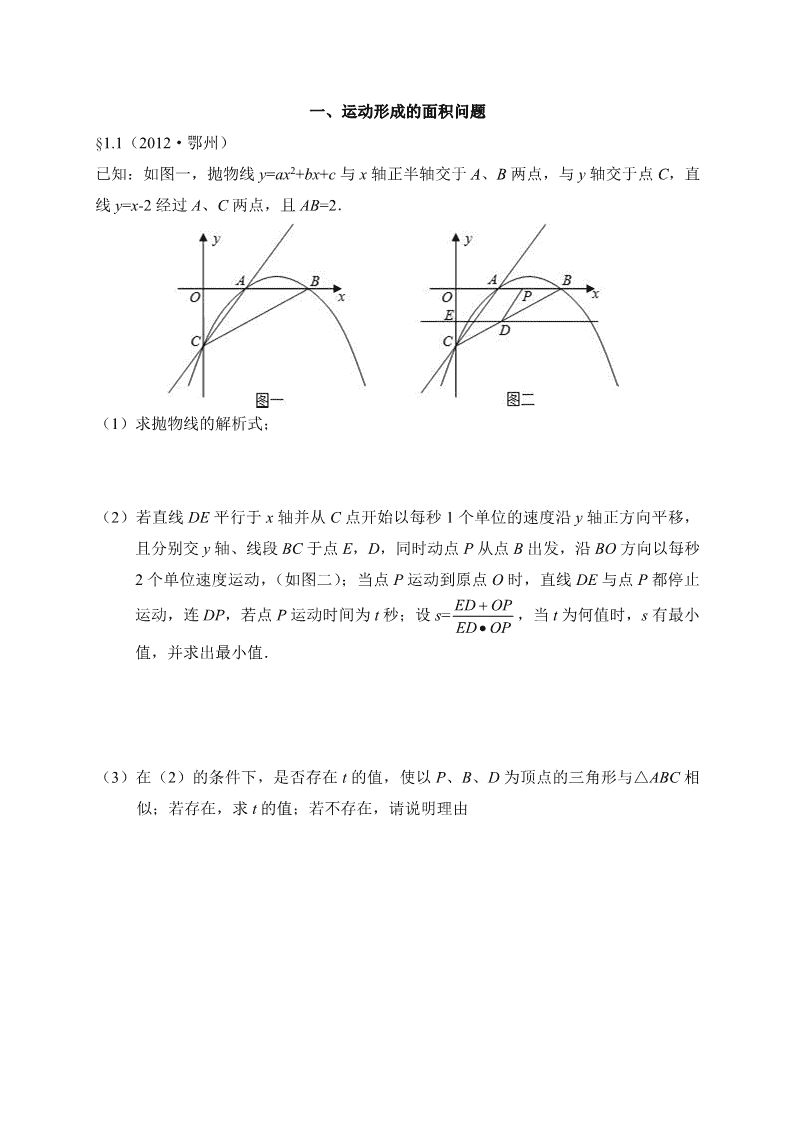
一、运动形成的面积问题 §1.1（2012·鄂州） 已知：如图一，抛物线 y=ax2+bx+c 与 x 轴正半轴交于 A、B 两点，与 y 轴交于点 C，直 线 y=x-2 经过 A、C 两点，且 AB=2． （1）求抛物线的解析式； （2）若直线 DE 平行于 x 轴并从 C 点开始以每秒 1 个单位的速度沿 y 轴正方向平移， 且分别交 y 轴、线段 BC 于点 E，D，同时动点 P 从点 B 出发，沿 BO 方向以每秒 2 个单位速度运动，（如图二）；当点 P 运动到原点 O 时，直线 DE 与点 P 都停止 运动，连 DP，若点 P 运动时间为 t 秒；设 s= OPED OPED   ，当 t 为何值时，s 有最小 值，并求出最小值． （3）在（2）的条件下，是否存在 t 的值，使以 P、B、D 为顶点的三角形与△ABC 相 似；若存在，求 t 的值；若不存在，请说明理由 §1.2（2013·资阳） 如图，四边形 ABCD 是平行四边形，过点 A、C、D 作抛物 线 y=ax2+bx+c(a≠0)，与 x 轴的另一交点为 E，连结 CE，点 A、 B、D 的坐标分别为(-2,0)、(3,0)、(0,4)． （1）求抛物线的解析式； （2）已知抛物线的对称轴 l 交 x 轴于点 F，交线段 CD 于点 K，点 M、N 分别是直线 l 和 x 轴上的动点，连结 MN，当线段 MN 恰好被 BC 垂直平分时，求点 N 的坐标； （3）在满足（2）的条件下，过点 M 作一条直线，使之将四边形 AECD 的面积分为 3:4 的两部分，求出该直线的解析式． §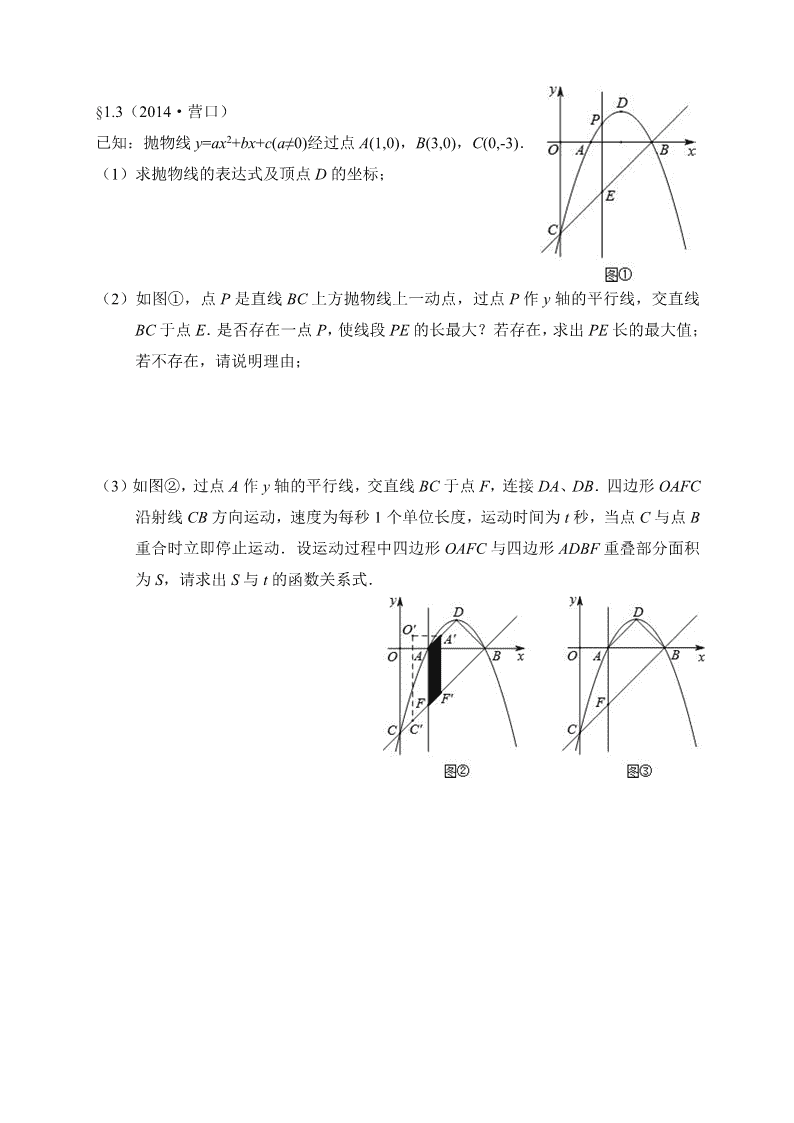1.3（2014·营口） 已知：抛物线 y=ax2+bx+c(a≠0)经过点 A(1,0)，B(3,0)，C(0,-3)． （1）求抛物线的表达式及顶点 D 的坐标； （2）如图①，点 P 是直线 BC 上方抛物线上一动点，过点 P 作 y 轴的平行线，交直线 BC 于点 E．是否存在一点 P，使线段 PE 的长最大？若存在，求出 PE 长的最大值； 若不存在，请说明理由； （3）如图②，过点 A 作 y 轴的平行线，交直线 BC 于点 F，连接 DA、DB．四边形 OAFC 沿射线 CB 方向运动，速度为每秒 1 个单位长度，运动时间为 t 秒，当点 C 与点 B 重合时立即停止运动．设运动过程中四边形 OAFC 与四边形 ADBF 重叠部分面积 为 S，请求出 S 与 t 的函数关系式． §1.4（2015·重庆 A） 如图 1，在平面直角坐标系中，抛物线 3334 3 2  xy 交 x 轴于 A，B 两点（点 A 在点 B 的左侧），交 y 轴于点 W， 顶点为 C，抛物线的对称轴与 x 轴的交点为 D． （1）求直线 BC 的解析式； （2）点 E(m,0)，F(m+2,0)为 x 轴上两点，其中 2＜m＜4，EE'，FF'分别垂直于 x 轴，交 抛物线于点 E'，F'，交 BC 于点 M，N，当 ME'+NF'的值最大时，在 y 轴上找一点 R，使|RF'-RE'|的值最大，请求出 R 点的坐标及|RF'-RE'|的最大值； （3）如图 2，已知 x 轴上一点 P( 2 9 ,0)，现以 P 为顶点，2 3 为边长在 x 轴上方作等边 三角形 QPG，使 GP⊥x 轴，现将△QPG 沿 PA 方向以每秒 1 个单位长度的速度平 移，当点 P 到达点 A 时停止，记平移后的△QPG 为△Q'P'G'．设△Q'P'G'与△ADC 的重叠部分面积为 s．当 Q'到 x 轴的距离与点 Q'到直线 AW 的距离相等时，求 s 的 值． 二、运动形成的最值问题 §2.1（2010·永州） 探究问题： （1）阅读理解： ①如图（A），在已知△ABC 所在平面上存在一点 P，使它到三 角形顶点的距离之和最小，则称点 P 为△ABC 的费马点，此 时 PA+PB+PC 的值为△ABC 的费马距离； ②如图（B），若四边形 ABCD 的四个顶点在同一圆上，则有 AB•CD+BC•DA=AC•BD．此为托勒密定理； （2）知识迁移： ①请你利用托勒密定理，解决如下问题：如图（C），已知点 P 为等边△ABC 外接 圆的 ︵ BC上任意一点．求证：PB+PC=PA； ②根据（2）①的结论，我们有如下探寻△ABC（其中∠A、∠B、 ∠C 均小于 120°）的费马点和费马距离的方法： 第一步：如图（D），在△ABC 的外部以 BC 为边长等边△BCD 及其外接圆； 第二步：在 ︵ BC上任取一点 P'，连接 P'A、P'B、P'C、P'D．易知 P'A+P'B+P'C=P'A+(P'B+P'C) =P'A+_______； 第三步：请你根据（1）①中定义，在图（D）中找出△ABC 的 费马点 P，并请指出线段________的长度即为△ABC 的费马距离． （3）知识应用： 2010 年 4 月，我国西南地区出现了罕见的持续干旱现象，许多村庄出现了人、 畜饮水困难，为解决老百姓的饮水问题，解放军某部来到云南某地打井取水． 已知三村庄 A、B、C 构成了如图（E）所示的△ABC（其中∠A、∠B、∠C 均小于 120°），现选取一点 P 打水井，使从水井 P 到三村庄 A、B、C 所铺设的输 水管总长度最小，求输水管总长度的最小值． §2.2（2011·丹东） 己知：二次函数 y=ax2+bx+6(a≠0)与 x 轴交于 A、B 两点（点 A 在点 B 的左侧），点 A、 点 B 的横坐标是一元二次方程 x2-4x-12=0 的两个根． （1）请直接写出点 A、点 B 的坐标． （2）请求出该二次函数表达式及对称轴和顶点坐标． （3）如图 1，在二次函数对称轴上是否存在点 P，使△APC 的周长最小，若存在，请求 出点 P 的坐标；若不存在，请说明理由． （4）如图 2，连接 AC、BC，点 Q 是线段 0B 上一个动点（点 Q 不与点 O、B 重合）．过 点 Q 作 QD∥AC 交 BC 于点 D，设 Q 点坐标(m,0)，当△CDQ 面积 S 最大时，求 m 的值． §2.3（2014·重庆 B） 如图 1，在□ABCD 中，AH⊥ DC，垂足为 H，AB=4 7 ， AD=7，AH= 21 ．现有两个 动点 E，F 同时从点 A 出发， 分别以每秒 1 个单位长度、每 秒 3 个单位长度的速度沿射线 AC 方向匀速运动，在点 E，F 的运动过程中，以 EF 为边 作等边△EFG，使△EFG 与△ABC 在射线 AC 的同侧，当点 E 运动到点 C 时，E，F 两 点同时停止运动，设运动时间为 t 秒． （1）求线段 AC 的长； （2）在整个运动过程中，设等边△EFG 与△ABC 重叠部分的面积为 S，请直接写出 S 与 t 之间的函数关系式，并写出相应的自变量 t 的取值范围； （3）当等边△EFG 的顶点 E 到达点 C 时，如图 2，将△EFG 绕着点 C 旋转一个角度α （0°＜α＜360°），在旋转过程中，点 E 与点 C 重合，F 的对应点为 F'，G 的对应 点为 G'，设直线 F'G'与射线 DC、射线 AC 分别相交于 M，N 两点．试问：是否存 在点 M，N，使得△CMN 是以∠MCN 为底角的等腰三角形？若存在，请求出 CM 的长度；若不存在，请说明理由． §2.4（2015·福州） 如图，抛物线 y=x2-4x 与 x 轴交于 O，A 两点，P 为抛物线上 一点，过点 P 的直线 y=x+m 与对称轴交于点 Q． （1）这条抛物线的对称轴是________，直线 PQ 与 x 轴所夹 锐角的度数是_________； （2）若两个三角形面积满足 S△POQ= 3 1 S△PAQ，求 m 的值； （3）当点 P 在 x 轴下方的抛物线上时，过点 C(2,2)的直线 AC 与直线 PQ 交于点 D，求： ①PD+DQ 的最大值； ②PD•DQ 的最大值． 三、运动形成的存在性问题 §3.1（2014·莆田） 如图，在边长为 4 的正方形 ABCD 中，动点 E 以每秒 1 个单位长度的速度从点 A 开始 沿边 AB 向点 B 运动，动点 F 以每秒 2 个单位长度的速度从点 B 开始沿折线 BC—CD 向 点 D 运动，动点 E 比动点 F 先出发 1 秒，其中一个动点到达终点时，另一个动点也随 之停止运动，设点 F 的运动时间为 t 秒． （1）点 F 在边 BC 上． ①如图 1，连接 DE，AF，若 DE⊥AF，求 t 的值； ②如图 2，连结 EF，DF，当 t 为何值时，△EBF 与△DCF 相似？ （2）如图 3，若点 G 是边 AD 的中点，BG，EF 相交于点 O，试探究：是否存在在某一 时刻 t，使得 1 6 BO =OG ？若存在，求出 t 的值；若不存在，请说明理由． §3.2（2012·襄阳） 如图，在矩形 OABC 中，AO=10，AB=8，沿直线 CD 折叠矩形 OABC 的一边 BC，使点 B 落在 OA 边上的点 E 处．分别以 OC，OA 所在的 直线为 x 轴，y 轴建立平面直角坐标系，抛物线 y=ax2+bx+c 经过 O， D，C 三点． （1）求 AD 的长及抛物线的解析式； （2）一动点 P 从点 E 出发，沿 EC 以每秒 2 个单位长的速度向点 C 运动，同时动点 Q 从点 C 出发，沿 CO 以每秒 1 个单位长的速度向点 O 运动，当点 P 运动到点 C 时， 两点同时停止运动．设运动时间为 t 秒，当 t 为何值时，以 P、Q、C 为顶点的三 角形与△ADE 相似？ （3）点 N 在抛物线对称轴上，点 M 在抛物线上，是否存在这样的点 M 与点 N，使以 M， N，C，E 为顶点的四边形是平行四边形？若存在，请直接写出点 M 与点 N 的坐标 （不写求解过程）；若不存在，请说明理由． §3.3（2013·恩施州） 如图所示，直线 l：y=3x+3 与 x 轴交于点 A，与 y 轴交于 点 B．把△AOB 沿 y 轴翻折，点 A 落到点 C，抛物线过点 B、C 和 D(3,0)． （1）求直线 BD 和抛物线的解析式． （2）若 BD 与抛物线的对称轴交于点 M，点 N 在坐标轴上，以点 N、B、D 为顶点的三 角形与△MCD 相似，求所有满足条件的点 N 的坐标． （3）在抛物线上是否存在点 P，使 S△PBD=6？若存在，求出点 P 的坐标；若不存在，说 明理由． §3.4（2013·贵港） 如图，在平面直角坐标系 xOy 中，抛物线 y=ax2+bx+c 交 y 轴于点 C(0,4)，对称轴 x=2 与 x 轴交于点 D，顶点为 M，且 DM=OC+OD． （1）求该抛物线的解析式； （2）设点 P(x,y)是第一象限内该抛物线上的一个动点，△PCD 的面积为 S，求 S 关于 x 的函数关系式，并写出自变量 x 的取值范围； （3）在（2）的条件下，若经过点 P 的直线 PE 与 y 轴交于点 E，是否存在以 O、P、E 为顶点的三角形与△OPD 全等？若存在，请求出直线 PE 的解析式；若不存在， 请说明理由． §3.5（2013·湖州） 如图①，O 为坐标原点，点 B 在 x 轴的正半轴上，四边形 OACB 是平行四边形，sin∠AOB= 5 4 ，反比例函数 y= x k (k＞0)在第一 象限内的图象经过点 A，与 BC 交于点 F． （1）若 OA=10，求反比例函数解析式； （2）若点 F 为 BC 的中点，且△AOF 的面积 S=12，求 OA 的长和点 C 的坐标； （3）在（2）中的条件下，过点 F 作 EF∥OB，交 OA 于点 E（如图②），点 P 为直线 EF 上的一个动点，连接 PA，PO．是否存在这样的点 P，使以 P、O、A 为顶点的 三角形是直角三角形？若存在，请直接写出所有点 P 的坐标；若不存在，请说明 理由． §3.6（2013·临沂） 如图，抛物线经过 A(-1,0)，B(5,0)，C(0,- 2 5 )三点． （1）求抛物线的解析式； （2）在抛物线的对称轴上有一点 P，使 PA+PC 的值最小，求点 P 的坐标； （3）点 M 为 x 轴上一动点，在抛物线上是否存在一点 N，使以 A，C，M，N 四点构成 的四边形为平行四边形？若存在，求点 N 的坐标；若不存在，请说明理由． §3.7（2012·北海） 如图，在平面直角坐标系中有 Rt△ABC，∠A=90°， AB=AC，A(-2,0)、B(0,1)、C(d,2)． （1）求 d 的值； （2）将△ABC 沿 x 轴的正方向平移，在第一象限内 B、C 两点的对应点 B'、C'正好落 在某反比例函数图象上．请求出这个反比例函数和此时的直线 B'C'的解析式； （3）在（2）的条件下，直线 BC 交 y 轴于点 G．问是否存在 x 轴上的点 M 和反比例函 数图象上的点 P，使得四边形 PGMC'是平行四边形？如果存在，请求出点 M 和点 P 的坐标；如果不存在，请说明理由． §3.8（2015·雅安） 如图，已知抛物线 C1：y=- 2 1 x2，平移抛物线 y=x2，使其顶点 D 落在抛物线 C1 位于 y 轴右侧的图象上，设平移后的抛物线 为 C2，且 C2 与 y 轴交于点 C(0,2)． （1）求抛物线 C2 的解析式； （2）抛物线 C2 与 x 轴交于 A，B 两点（点 B 在点 A 的右侧），求点 A，B 的坐标及过点 A，B，C 的圆的圆心 E 的坐标； （3）在过点(0, 2 1 )且平行于 x 轴的直线上是否存在点 F，使四边形 CEBF 为菱形？若存 在，求出点 F 的坐标；若不存在，请说明理由． 四、运动形成的几何定值、恒等问题 §4.1（2010·镇江） 对非负实数 x“四舍五入”到个位的值记为＜x＞，即：当 n 为非负整数时，如果 n− 2 1 ≤ x＜n+ 2 1 ，则＜x＞=n． 如：＜0＞=＜0.48＞=0，＜0.64＞=＜1.493＞=1，＜2＞=2，＜3.5＞=＜4.12＞=4，… 试解决下列问题： （1）填空：①＜π＞=________（π为圆周率）； ②如果＜2x-1＞=3，则实数 x 的取值范围为____________； （2）①当 x≥0，m 为非负整数时，求证：＜x+m＞=m+＜x＞； ②举例说明＜x+y＞=＜x＞+＜y＞不恒成立； （3）求满足＜x＞= 3 4 x 的所有非负实数 x 的值； （4）设 n 为常数，且为正整数，函数 y=x2−x+ 4 1 的自变量 x 在 n≤x＜n+1 范围内取值时， 函数值 y 为整数的个数记为 a，满足＜k＞=n 的所有整数 k 的个数记为 b．求证： a=b=2n． §4.2（2012·广州） 如图，抛物线 y=- 8 3 x2- 4 3 x+3 与 x 轴交于 A、B 两点（点 A 在点 B 的左侧），与 y 轴交于点 C． （1）求点 A、B 的坐标； （2）设 D 为已知抛物线的对称轴上的任意一点，当△ACD 的面积等于△ACB 的面积时， 求点 D 的坐标； （3）若直线 l 过点 E(4,0)，M 为直线 l 上的动点，当以 A、B、M 为顶点所作的直角三 角形有且只有三个时，求直线 l 的解析式． §4.3（2012·义乌市） 如图 1，已知直线 y=kx 与抛物线 3 22 27 4 2  xy 交于 点 A (3,6)． （1）求直线 y=kx 的解析式和线段 OA 的长度； （2）点 P 为抛物线第一象限内的动点，过点 P 作直线 PM，交 x 轴于点 M（点 M、O 不重合），交直线 OA 于点 Q，再过点 Q 作直线 PM 的垂线，交 y 轴于点 N．试探 究：线段 QM 与线段 QN 的长度之比是否为定值？如果是，求出这个定值；如果 不是，说明理由； （3）如图 2，若点 B 为抛物线上对称轴右侧的点，点 E 在线段 OA 上（与点 O、A 不重 合），点 D(m,0)是 x 轴正半轴上的动点，且满足∠BAE=∠BED=∠AOD．继续探究： m 在什么范围时，符合条件的 E 点的个数分别是 1 个、2 个？ §4.4（2013·鄂州） 在平面直角坐标系中，已知 M1(3,2)，N1(5,-1)，线段 M1N1 平 移至线段 MN 处（注：M1 与 M，N1 与 N 分别为对应点）． （1）若 M(-2,5)，请直接写出 N 点坐标． （2）在（1）问的条件下，点 N 在抛物线 y= 6 1 x2+ 3 32 x+k 上，求该抛物线对应的函数 解析式． （3）在（2）问条件下，若抛物线顶点为 B，与 y 轴交于点 A，点 E 为线段 AB 中点， 点 C(0,m)是 y 轴负半轴上一动点，线段 EC 与线段 BO 相交于 F，且 OC:OF=2: 3 ， 求 m 的值． （4）在（3）问条件下，动点 P 从 B 点出发，沿 x 轴正方向匀速运动，点 P 运动到什么 位置时（即 BP 长为多少），将△ABP 沿边 PE 折叠，△APE 与△PBE 重叠部分的 面积恰好为此时的△ABP 面积的 4 1 ，求此时 BP 的长度．