- 3.64 MB
- 2021-05-27 发布
1.什么叫全等三角形? 全等三角形的
对应边、对应角有什么重要性质?
2. 我们已经学过如何判断两个三角形
是全等三角形,你能说说他的判定条
件是什么?
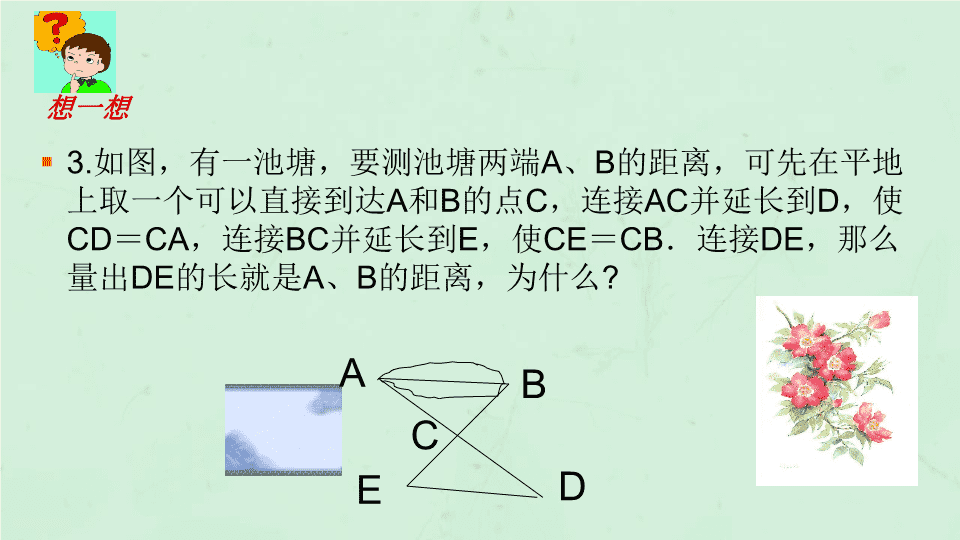
§ 3.如图,有一池塘,要测池塘两端A、B的距离,可先在平地
上取一个可以直接到达A和B的点C,连接AC并延长到D,使
CD=CA,连接BC并延长到E,使CE=CB.连接DE,那么
量出DE的长就是A、B的距离,为什么?
A B
C
DE
想一想
合作探究
§ (一)例2 已知:如图,AB、CD相交于点E,且
§ E是AB、CD 的中点.
§ 求证:①△AEC ≌△BED . ②AC∥DB.
�
C
�
B
�
A
�
D
�
E
§ (二)例3 已知:如图,点E、F在CD上,且CE =DF,
§ AE =BF, AE ∥BF.
§ ①求证:△AEC ≌△BFD .
§ ②你还能证得其他新的结论吗? �
F
�
C
�
B
�
A
�
D
�
E
§ 1、已知,如图,C是AB的中点AE=BD,∠A=∠B,
§ 求证:∠E=∠D
§ 证明:∵C是AB的中点(已知)
§ ∴ = ( )
§ 在△ABC和△BDC中
§ ∴△AEC≌△BDC( )
§ ∴∠E=∠D( )
§ 2、已知,如图,点D在AE上,BD=CD,∠BDE=∠CDE
§ 求证:AB=AC
§ 证明:∵∠BDE+∠ =180°
§ ∠CDE+∠ =180°(平角的定义)
§ ∠BDE=∠CDE(已知)
§ ∴∠ =∠ ( )
§ 在△ABD和△ACD中
∴△ABD≌ △ACD( )
§ ∴AB=AC( )
§ 3. 已知CE=CB,∠1=∠2,AC=DC,求证:
△ABC≌△DEC;
B
E
C
D
A
1
2
§ 4. 是 中边的中点, ,且.
§ 求证:⑴ ≌ ⑵
D ABC ACDABD ACAB
ABD ACD ECEB
§ 如图, 和 都是等边三角形,连接 、 交
于点 O .
§ 求证:⑴ ⑵
ABCECD BE AD
BEAD 60AOB
1. 如图,已知AB=AD,那么添加下列一个
条件后,能用SAS判定△ABC≌△ADC的
是( )
A.CB=CD B.∠BAC=∠DAC
C.∠BCA=∠DCA D.∠B=∠D=90°
2. 如图,AB=AC,添加下列条件,能用
SAS判断△ABE≌△ACD的是( )
A.∠B=∠C B.∠AEB=∠ADC
C.AE=AD D.BE=DC
爱学数学
爱数学周报再见
相关文档
- 八年级上数学课件《平面直角坐标系2021-05-27 21:02:2724页
- 八年级下数学课件《反比例函数》 2021-05-27 20:54:1618页
- 八年级上数学课件《勾股定理》 (122021-05-27 20:23:5118页
- 八年级上数学课件- 14-2-1 平方差2021-05-27 20:02:1726页
- 八年级下数学课件《分式的基本性质2021-05-27 19:56:5212页
- 八年级上数学课件八年级上册数学课2021-05-27 19:56:009页
- 七年级下数学课件《图形的平移》 (2021-05-27 19:50:5718页
- 七年级下数学课件《单项式乘多项式2021-05-27 19:46:4018页
- 八年级上数学课件八年级上册数学课2021-05-27 19:23:1411页
- 八年级上数学课件- 11-2-1 三角形2021-05-27 19:21:0618页