【数学】2020届一轮复习人教A版 相似三角形的判定与性质 课时作业 8页

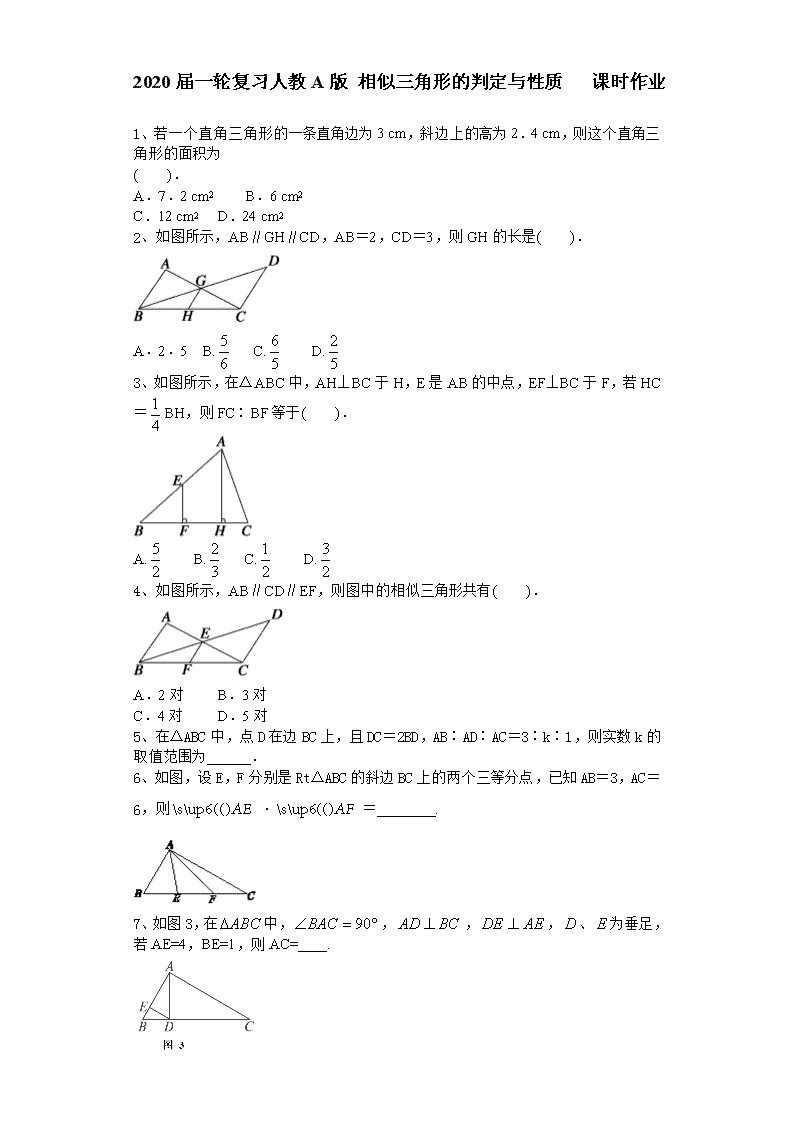
‎2020届一轮复习人教A版 相似三角形的判定与性质 课时作业 ‎ 1、若一个直角三角形的一条直角边为3 cm，斜边上的高为2．4 cm，则这个直角三角形的面积为 ‎(　　)．‎ A．7．2 cm2 B．6 cm2‎ C．12 cm2 D．24 cm2‎ ‎2、如图所示，AB∥GH∥CD，AB＝2，CD＝3，则GH的长是(　　)．‎ A．2．5 B. C. D.‎ ‎3、如图所示，在△ABC中，AH⊥BC于H，E是AB的中点，EF⊥BC于F，若HC＝BH，则FC∶BF等于(　　)．‎ A. B. C. 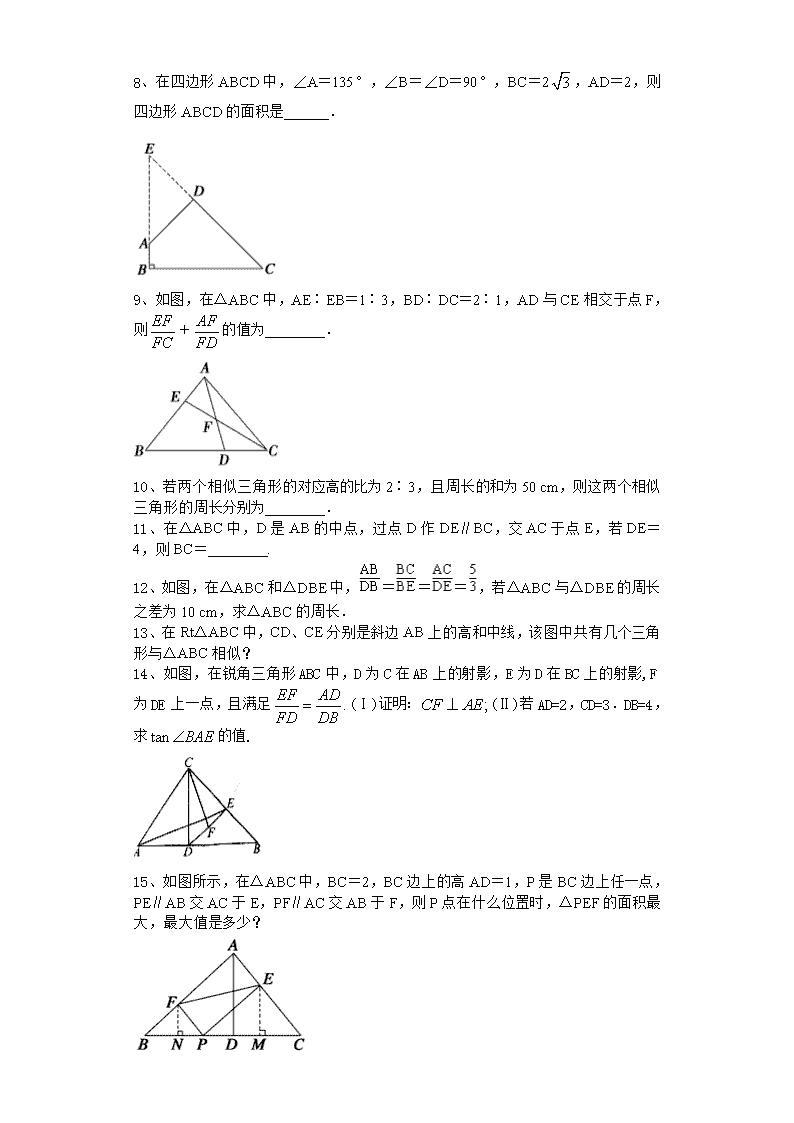D.‎ ‎4、如图所示，AB∥CD∥EF，则图中的相似三角形共有(　　)．　　　　　　　　　　　　　　　　‎ A．2对 B．3对 C．4对 D．5对 5、在△ABC中，点D在边BC上，且DC＝2BD，AB∶AD∶AC＝3∶k∶1，则实数k的取值范围为 ．‎ ‎6、如图，设E，F分别是Rt△ABC的斜边BC上的两个三等分点，已知AB＝3，AC＝6，则·＝ .‎ ‎7、如图3，在中，，，，、为垂足，若AE=4，BE=1，则AC= .‎ ‎8、在四边形ABCD中，∠A＝135°，∠B＝∠D＝90°，BC＝2，AD＝2，则四边形ABCD的面积是______．‎ ‎9、如图，在△ABC中，AE∶EB＝1∶3，BD∶DC＝2∶1，AD与CE相交于点F，则＋的值为________．‎ ‎10、若两个相似三角形的对应高的比为2∶3，且周长的和为50 cm，则这两个相似 三角形的周长分别为________．‎ ‎11、在△ABC中，D是AB的中点，过点D作DE∥BC，交AC于点E，若DE＝4，则BC＝________. 12、如图，在△ABC和△DBE中，＝＝＝，若△ABC与△DBE的周长之差为10 cm，求△ABC的周长．‎ ‎13、在Rt△ABC中，CD、CE分别是斜边AB上的高和中线，该图中共有几个三角形与△ABC相似？‎ ‎14、如图，在锐角三角形ABC中，D为C在AB上的射影，E为D在BC上的射影,F为DE上一点，且满足(Ⅰ)证明：(Ⅱ)若AD=2，CD=3．DB=4，求的值.‎ ‎15、如图所示，在△ABC中，BC＝2，BC边上的高AD＝1，P是BC边上任一点，PE∥AB交AC于E，PF∥AC交AB于F，则P点在什么位置时，△PEF的面积最大，最大值是多少？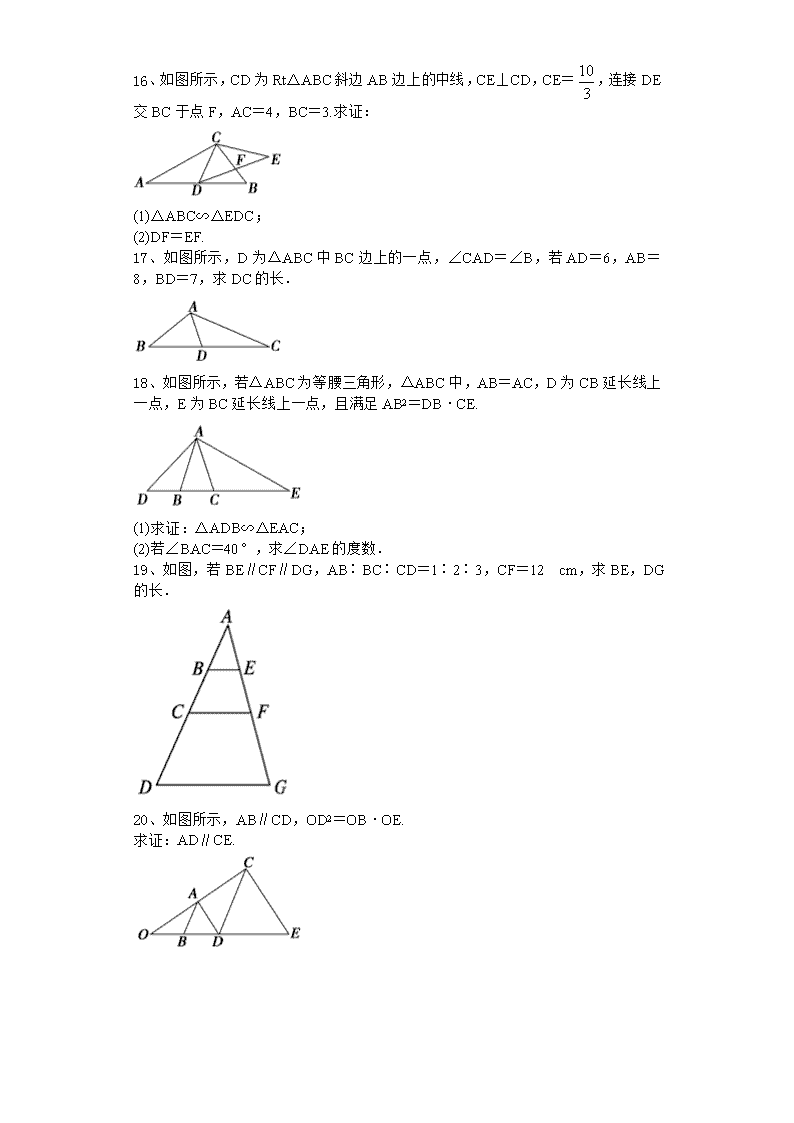‎ ‎16、如图所示，CD为Rt△ABC斜边AB边上的中线，CE⊥CD，CE＝，连接DE交BC于点F，AC＝4，BC＝3.求证：‎ ‎ ‎ ‎(1)△ABC∽△EDC；‎ ‎(2)DF＝EF.‎ ‎17、如图所示，D为△ABC中BC边上的一点，∠CAD＝∠B，若AD＝6，AB＝8，BD＝7，求DC的长．‎ ‎18、如图所示，若△ABC为等腰三角形，△ABC中，AB＝AC，D为CB延长线上一点，E为BC延长线上一点，且满足AB2＝DB·CE.‎ ‎(1)求证：△ADB∽△EAC；‎ ‎(2)若∠BAC＝40°，求∠DAE的度数．‎ ‎19、如图，若BE∥CF∥DG，AB∶BC∶CD＝1∶2∶3，CF＝12 cm，求BE，DG的长．‎ ‎20、如图所示，AB∥CD，OD2＝OB·OE.‎ 求证：AD∥CE.‎ 参考答案 ‎1、答案：B 长为3 cm的直角边在斜边上的射影为＝1．8 (cm)，故由射影定理知斜边长为＝5 (cm)，∴三角形的面积为×5×2．4＝6 (cm2)．‎ ‎2、答案：C ‎∵AB∥GH，∴＝，‎ ‎∵GH∥CD，∴＝，‎ ‎∴＋＝＋＝1，∴GH＝.‎ ‎3、答案：D 由AH⊥BC，EF⊥BC知EF∥AH，又∵AE＝EB，‎ ‎∴BF＝FH，∴HC＝BH＝BF，∴FC＝BF.‎ ‎4、答案：B 5、答案：(，) 6、答案：10 7、答案：10 8、答案：4‎ 因∠B＝∠D＝90°，于是设想构造直角三角形，延长BA与CD的延长线交于E，则得到Rt△BCE和Rt△ADE，由题目条件知，△ADE为等腰直角三角形，所以DE＝AD＝2，所以S△ADE＝×2×2＝2.‎ 又可证Rt△EBC∽Rt△EDA，‎ 所以＝2＝2＝3.‎ ‎∴S△EBC＝3S△EDA，∴S四边形ABCD＝S△EBCS△ADE＝4.‎ ‎9、答案：‎ 过D作DG∥CE交AB于G，‎ 则＝＝，‎ 又∵＝，‎ ‎∴AE＝EG.‎ ‎∴＝＝1.‎ 又∵＝＝，‎ EF＝DG，‎ ‎∴＝.∴＝.‎ ‎∴＋＝.‎ ‎10、答案：20 cm,30 cm 设较大的三角形的周长为x cm，则较小的三角形的周长为(50x)cm.由题意得＝，解得x＝30,50x＝5030＝20.‎ ‎11、答案：8‎ ‎∵DE∥BC，∴△ADE∽△ABC.∴DE∶BC＝AD∶AB＝1∶2.∴BC＝2DE＝8.‎ ‎12、答案：利用相似三角形的相似比等于周长比可得△ABC的周长为25 cm. 13、答案：△ACD、△CBD与△ABC相似，共2个．‎ ‎ 14、答案：(Ⅰ)证明：设与交于点,连接.‎ ‎,,又△∽△,‎ ‎.于是有,注意到 C A B D E F Game ‎,∴△∽△,‎ ‎∴,∴四点共圆.从而有,‎ ‎∴.‎ ‎(Ⅱ)在△中,,‎ ‎,,,由,知,‎ ‎.又,.‎ 故. 15、答案：如图所示，作EM⊥BC于M，FN⊥BC于N，设BP＝x.‎ ‎∵PF∥AC，‎ ‎∴△BPF∽△BCA，‎ ‎∴＝，∴FN＝x.‎ 同理△PCE∽△BCA，EM＝(2x)．‎ ‎∴S△PEF＝S？AEPF＝(S△ABCS△BFPS△PEC)‎ ‎＝ ‎ ‎＝x2＋x＝(x1)2＋ (0