北师大版八年级下册数学专题训练课件-第1章 三角形的证明-1专题一 本章知识梳理 10页

中小学精品教学资源 中小学精品教学资源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中小学精品教学资源 中 小 学 精 品 教 学 资 源 中小学精品 学资源 中小学精品教学 源 中 小 学 精 品 教 学 资 源 中小学精品教学资源 中 小 学 精 品 教 学 资 源 中小学精品教学资源 中小学精品教学资源中小学精品教学资源 中小学精品教学资源 中 学精品教学资源 中 小 学 精 品 教 学 资 源 中小学精品教学资源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中小学精品教学资源 中小学精品教学资源 中小 精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源中 精品教学资源 中小 精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中小学精品 学资源 中 小 学 精 品 教 学 资 源 中小学精品教学资源 中小学精品教学资源中小学精品教学资源 中小学精品教学资源 中 学精品教学资源 中 精品教学资源 中小学精品教学资源 中小 品教学 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 资 源 中 小 精 品 教 学 资 源 中小学精品教 资源 中 小 学 精 品 教 学 资 源中小学精品教 资源 中 小 学 精 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 资 源 中 小 学 精 品 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中小学精品教学资源 中小学精 教学资中小学精品教学资 中小学精品教学资源 中小学精品教学资源 中小 精品教学资源 中小学 品教学资源 中小 精品教学资源 中小 精品教 资源 中小学精品教学资源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中小学精品教学 源 中 小 学 精 品 教 学 资 源 中小学精品 资源 中小学精品教学 源 中 小 学 精 品 教 学 资 源 中小学精品教学资源 中 小 学 精 品 教 学 资 源 小学精品教 资源 中小学精品教 资源中小学精品教学资源 学精品教学资源 中 学精 教学资源 中 小 学 精 品 教 学 资 源 中 学资源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中小学精品教学资源 中小学精品教学资源 中小 精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学 品教学资源中 精品教学资源 小 精品教学资源 中小学精品教学资源 中小学精品教学资源 中 学精品教学资 中小 精品教学资源 中小学精品教学资源 中小学精品 中小 精品教 资源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中小 精品 学资源 中 小 学 精 品 教 学 资 源 中小 精品 学资源 中 学精品教 资源中小 精品教学资源 中小学精品教学资源 中 学精品 资源 中 教学资源 中 精 教学资源 中小 品教学 源 中 小 学 精 品 教 学 资 源 小 学 精 品 教 学 资 源 中 小 学 品 教 资 源 中 小 学 品 教 资 源 中 小 品 教 资 源小学精品教 资 中 小 学 精 品 教 学 资 源中小学精品教 资 中 小 学 精 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 资 源 中 小 学 精 品 教 学 资 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 学 精 品 教 资 源 中 小 学 品 学 资 源 中 小 学 精 品 教 学 资 源 中 小 精 品 教 学 资 源 中小学精品教学资源 中小 精 教中小学精品教学 中小学精品教学资源 中小学 品教学资 中小 精品教学资源 中小 品教学资源 精品教学资源 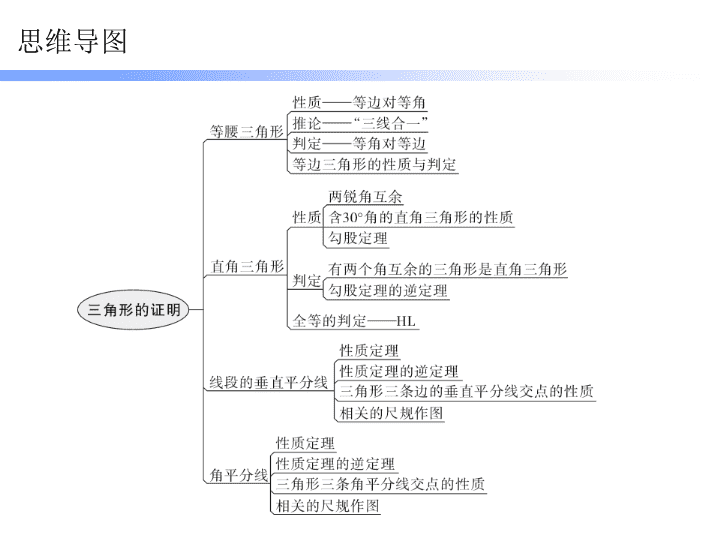第一章 三角形的证明 专题一 本章知识梳理 思维导图 1. 探索并掌握判定直角三角形全等的“斜边、直角边” 定理. 2. 探索并证明等腰三角形的性质定理：等腰三角形的两 个底角相等，底边上的高线、中线及顶角平分线重合； 探索并掌握等腰三角形的判定定理：有两个底角相等的 三角形是等腰三角形；探索等边三角形的性质定理：等 边三角形的各角都等于60°；探索等边三角形的判定定 理：三个角都相等的三角形(或有一个角是60°的等腰三 角形)是等边三角形. 课程标准 3. 探索并掌握直角三角形的性质定理：在直角三角形中， 如果一个锐角等于30°，那么它所对的直角边等于斜边 的一半. 4. 探索并证明线段垂直平分线的性质定理：线段垂直平 分线上的点到这条线段两个端点的距离相等；反之，到 线段两个端点的距离相等的点在这条线段的垂直平分线 上. 5. 探索并证明角平分线的性质定理：角平分线上的点到 这个角两边的距离相等；反之，在一个角的内部，到角 的两边距离相等的点在这个角的平分线上. 1. 等腰三角形的性质定理及推论 等腰三角形的两______相等，简称_____________. 等腰三角形顶角的___________、底边上的_______及底 边上的______互相重合（简称三线合一）. 2. 等边三角形的性质与判定 （1）性质定理：等边三角形的三个内角都_______，并 且每个角都等于______. （2）判定定理：①三个角都______的三角形是等边三角 形. ②有一个角等于______的等腰三角形是等边三角形. 知识梳理 底角 等边对等角 角平分线 中线 高线 相等 60° 相等 60° 3. 反证法 （1）在证明时，先假设命题的结论________，然后推导 出与定义、基本事实、已有定理或已知条件相_______的 结果，从而证明命题的结论一定______. 这种证明方法 称为反证法. （2）用反证法证明的一般步骤： ①假设命题的结论不成立（即假设命题的结论的反面成 立）. ②对该假设进行推理论证，得出与定义、基本事实、已 有定理或已知条件相矛盾的结果. ③由此判定假设不成立，而原命题的结论成立. 不成立 矛盾 成立 4. 含30°角的直角三角形的性质定理 在直角三角形中，如果一个锐角等于30°，那么它所对 的直角边等于______________. 5. 逆命题、互逆命题、逆定理、互逆定理 （1）在两个命题中，如果一个命题的条件和结论分别是 另一个命题的______________，那么这两个命题称为 __________，其中一个命题称为另一个命题的 __________. （2）如果一个定理的逆命题经过证明是________，那么 它也是一个定理，这两个定理称为___________，其中一 个定理称为另一个定理的________. 斜边的一半 结论和条件 互逆命题 逆命题 真命题 互逆定理 逆定理 6. 线段垂直平分线 （1）线段垂直平分线的性质定理 线段垂直平分线上的点到这条线段____________的距离 相等. （2）线段垂直平分线性质定理的逆定理 到一条线段___________距离相等的点，在这条线段的 ____________上. （3）三角形三条边的垂直平分线交点的性质 三角形三条边的_____________相交于一点，并且这一点 到___________的距离相等. 两个端点 两个端点 垂直平分线 垂直平分线 三个顶点 7. 角平分线 （1）角平分线的性质定理 角平分线上的点到这个角的________的距离相等. （2）角平分线性质定理的逆定理 在一个角的内部，到角的_______距离相等的点在这个角 的_________上. （3）三角形三条角平分线交点的性质 三角形的三条___________相交于一点，并且这一点到 __________的距离相等. 两边 两边 平分线 角平分线 三条边