- 118.50 KB
- 2021-05-25 发布
1.在同一平面内,不重合的两条直线的位置关系有_______种,分别是________.
2.(经典题)设 a,b,c为平面内三条不同直线:
(1)若 a∥b,c⊥a,则 b与 c的位置关系是______;
(2)若 a∥b,b∥c,则 a与 c的位置关系是______.
3.(合作探究题)在同一平面内三条直线交点有多少个?
甲:同一平面三直线相交交点的个数为 0个,因为 a∥b∥c,如图(1)所示.
乙:同一平面内三条直线交点个数只有 1个,因为 a,b,c交于同一点 O,如图(2)所示.
以上说法谁对谁错?为什么?
4.如图所示,在 5×5的网格中,AC是网格中最长的线段,请画出两条线段与 AC平行并且
过网格的格点.
5.(教材变式题)“垂直于同一条直线的两直线平行”,运用这一性质可以说明铺设铁轨互相
平行的道理.
如图所示,已知∠2是直角,再度量出∠1或∠3就会知道铁轨平行不平行?
[解答]
方案一:若量得∠3=90°,结合∠2情况,说明理由.
方案二:若量得∠1=90°,结合∠2情况,说明理由.
答案
1.2,相交,平行
2.(1)b⊥C (2)a∥c(点拨:画图来判定)
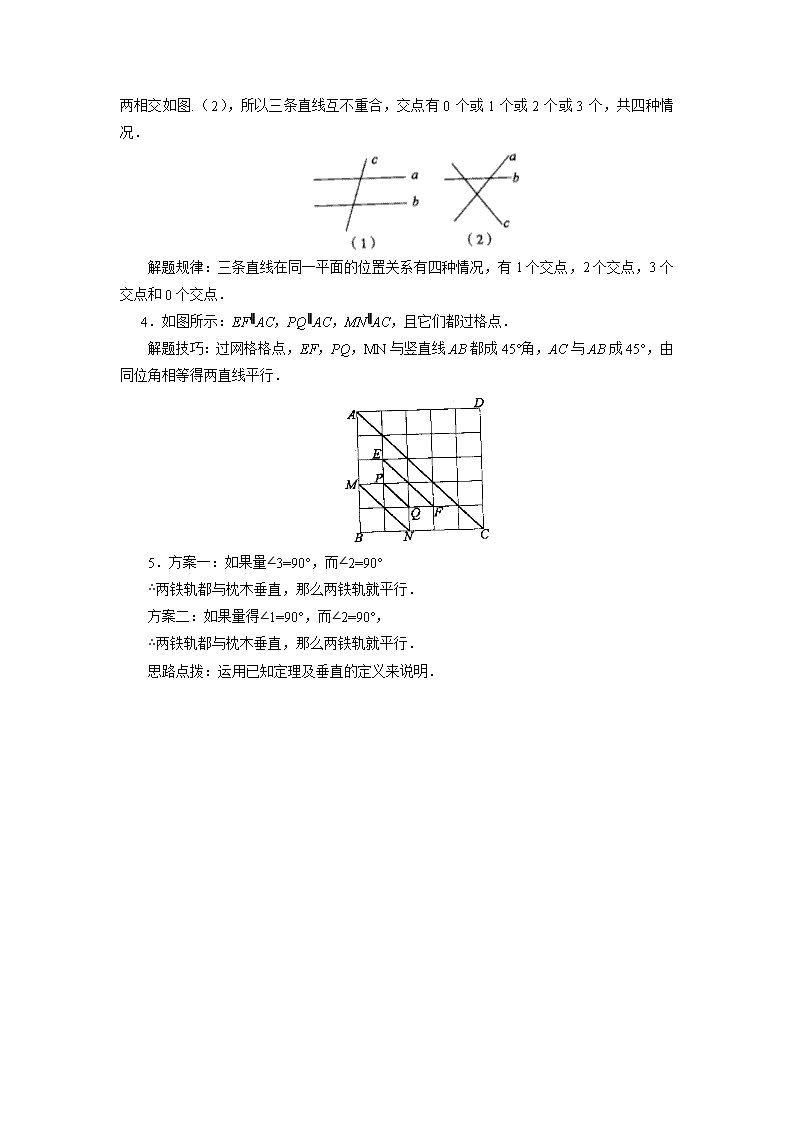
3.甲,乙说法都不对,各自少了三种情况.a∥b,c与 a,b相交如图(1),a,b,c
两两相交如图.(2),所以三条直线互不重合,交点有 0个或 1 个或 2个或 3 个,共四种情
况.
解题规律:三条直线在同一平面的位置关系有四种情况,有 1个交点,2个交点,3个
交点和 0个交点.
4.如图所示:EF∥AC,PQ∥AC,MN∥AC,且它们都过格点.
解题技巧:过网格格点,EF,PQ,MN与竖直线 AB都成 45°角,AC与 AB成 45°,由
同位角相等得两直线平行.
5.方案一:如果量∠3=90°,而∠2=90°
∴两铁轨都与枕木垂直,那么两铁轨就平行.
方案二:如果量得∠1=90°,而∠2=90°,
∴两铁轨都与枕木垂直,那么两铁轨就平行.
思路点拨:运用已知定理及垂直的定义来说明.
相关文档
- 新北师大版一年级数学上册同步练习2021-05-25 16:15:362页
- 七年级数学合并同类项 同步练习(三2021-05-25 16:08:463页
- 2020-2021学年高二数学上册同步练2021-05-25 16:08:2711页
- 人教版历史八上《抗击八国联军》同2021-05-25 15:59:224页
- 人教版化学九下《酸和碱的中和反应2021-05-25 15:57:529页
- 华师版数学八年级上册同步练习课件2021-05-25 15:53:1917页
- 北师大版高中数学选修1-1同步练习2021-05-25 15:52:003页
- 人教版语文五年级下册第3单元第102021-05-25 15:47:525页
- 湘教版初中地理七年级-亚洲及欧洲-2021-05-25 15:24:244页
- 沪科版物理八上《快与慢》同步练习2021-05-25 14:57:177页