2019届二轮复习第3讲　力学中的曲线运动课件（61张）（全国通用） 61页

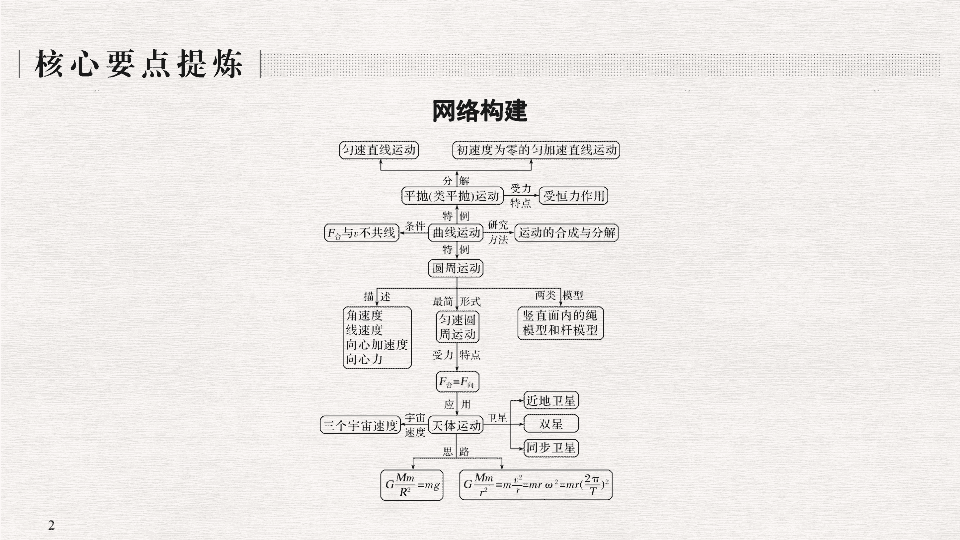
第 3 讲　力学中的曲线运动 网络构建 1 . 必须领会的 “ 四种物理思想和三种常用方法 ” ( 1) 分解思想、临界极值的思想、估算的思想、模型化思想 ( 2) 假设法、合成法、正交分解法 2 . 平抛 ( 或类平抛 ) 运动的推论 ( 1) 任意时刻速度的反向延长线一定通过此时水平位移的中点。 ( 2) 设在任意时刻瞬时速度与水平方向的夹角为 θ ，位移与水平方向的夹角为 φ ，则有 tan θ ＝ 2tan φ 。 备考策略 3 . 注意天体运动的三个区别 ( 1) 中心天体和环绕天体的区别 ( 2) 自转周期和公转周期的区别 ( 3) 星球半径和轨道半径的区别 4 . 记住天体运动中的 “ 三看 ” 和 “ 三想 ” ( 1) 看到 “ 近地卫星 ” 想到 “ 最大绕行速度 ”“ 最小周期 ” ( 2) 看到 “ 忽略地球自转 ” 想到 “ 万有引力等于重力 ” ( 3) 看到 “ 同步卫星 ” 想到 “ 周期 T ＝ 24 h ” 【典例 1 】 (2018· 北京理综， 20) 根据高中所学知识可知，做自由落体运动的小球，将落在正下方位置。但实际上，赤道上方 200 m 处无初速下落的小球将落在正下方位置偏东约 6 cm 处。这一现象可解释为，除重力外，由于地球自转，下落过程小球还受到一个水平向东的 “ 力 ” ，该 “ 力 ” 与竖直方向的速度大小成正比。现将小球从赤道地面竖直上抛，考虑对称性，上升过程该 “ 力 ” 水平向西，则小球 ( 　　 ) 运动的合成与分解及平抛运动 运动的合成与分解 A. 到最高点时，水平方向的加速度和速度均为零 B. 到最高点时，水平方向的加速度和速度均不为零 C. 落地点在抛出点东侧 D. 落地点在抛出点西 侧 解析　 由于该 “ 力 ” 与竖直方向的速度大小成正比，所以从小球抛出至运动到最高点过程，该 “ 力 ” 逐渐减小到零，将小球的上抛运动分解为水平和竖直两个分运动，由于上升阶段，水平分运动是向西的变加速运动 ( 水平方向加速度大小逐渐减小 ) ，故小球到最高点时速度不为零，水平向西的速度达到最大值，故选项 A 错误；小球到最高点时竖直方向的分速度为零，由题意可知小球这时不受水平方向的力，故小球到最高点时水平方向加速度为零，选项 B 错误；下降阶段，由于受水平向东的力，小球的水平分运动是向西的变减速运动 ( 水平方向加速度大小逐渐变大 ) ，由对称性可知，落地时水平速度恰为零，故小球的落地点在抛出点西侧，选项 C 错误， D 正确。 答案　 D 【典例 2 】 (2017· 全国卷 Ⅰ ， 15) 发球机从同一高度向正前方依次水平射出两个速度不同的乒乓球 ( 忽略空气的影响 ) 。速度较大的球越过球网，速度较小的球没有越过球网；其原因是 ( 　　 ) A . 速度较小的球下降相同距离所用的时间较多 B . 速度较小的球在下降相同距离时在竖直方向上的速度较大 C . 速度较大的球通过同一水平距离所用的时间较少 D . 速度较大的球在相同时间间隔内下降的距离较大 以 “ 体育运动 ” 为载体考查平抛运动的规律 答案　 C 解析　 小球做平抛运动，其运动轨迹如图所示。设斜面的倾角为 θ 。 斜面上的平抛运动 答案　 A 【典例 4 】 甲、乙两个同学对打乒乓球，设甲同学持拍的拍面与水平方向成 α 角，乙同学持拍的拍面与水平方向成 β 角，如图 1 所示，设乒乓球击打拍面时速度与拍面垂直，且乒乓球每次击打球拍前与击打后速度大小相等，不计空气阻力，则乒乓球击打甲的球拍的速度 v 1 与乒乓球击打乙的球拍的速度 v 2 之比为 ( 　　 ) 图 1 答案　 A 1. 图 2 中给出了某一通关游戏的示意图，安装在轨道 AB 上可上下移动的弹射器，能水平射出速度大小可调节的弹丸，弹丸射出口在 B 点的正上方。竖直面内的半圆弧 BCD 的半径 R ＝ 2.0 m ，直径 BD 水平且与轨道 AB 处在同一竖直面内，小孔 P 和圆心 O 连线与水平方向夹角为 37° 。游戏要求弹丸垂直于 P 点圆弧切线方向射入小孔 P 就能进入下一关。为了能通关，弹射器离 B 点的高度和弹丸射出的初速度分别是 ( 不计空气阻力， sin 37° ＝ 0.6 ， cos 37° ＝ 0.8 ) 图 2 答案　 A 2. ( 多选 ) 如图 3 所示， b 是长方形 acfd 对角线的交点， e 是底边 df 的中点， a 、 b 、 c 处的三个小球分别沿图示方向做平抛运动，落地后不反弹，下列表述正确的是 ( 　　 ) 图 3 A . 若 a 、 b 、 c 处三球同时抛出，三球可能在 de 之间的区域相遇 B . 只要 b 、 c 处两球同时开始做平抛运动，二者不可能在空中相遇 C . 若 a 、 b 处两球能在地面相遇，则 a 、 b 在空中运动的时间之比为 2 ∶ 1 D . 若 a 、 c 处两球在 e 点相遇，则一定满足 v a ＝ v c 答案　 BD 3. 一位网球运动员以拍击球，使网球由 O 点沿水平方向飞出，如图 4 所示，第一只球落在自己一方场地的 B 点，弹跳起来后，刚好擦网而过，落在 A 点，第二只球刚好擦网而过落在 A 点。设球与地面的碰撞过程没有能量损失，且运动过程不计空气阻力，则第一只与第二只球飞过球网 C 处时水平速度之比为 ( 　　 ) 图 4 A.1 ∶ 1 B.1 ∶ 3 C.3 ∶ 1 D.1 ∶ 9 解析　 由平抛运动的规律可知，两球分别被击出至各自第一次落地的时间相等。由于球与地面的碰撞是完全弹性碰撞，设第一只球自击出到落在 A 点时间为 t 1 ，第二只球自击出到落在 A 点时间为 t 2 ，则根据两球竖直方向的运动特点知 t 1 ＝ 3 t 2 ；由于两球在水平方向均做匀速运动，水平位移大小相等，由 x ＝ v 0 t 得，它们从 O 点出发时的初速度关系为 v 2 ＝ 3 v 1 ，所以第一只与第二只球飞过球网 C 处时水平速度之比为 1 ∶ 3 ，选项 B 正确。 答案　 B 【典例 1 】 (2016· 全国卷 Ⅱ ， 16) 小球 P 和 Q 用不可伸长的轻绳悬挂在天花板上， P 球的质量大于 Q 球的质量，悬挂 P 球的绳比悬挂 Q 球的绳短。将两球拉起，使两绳均被水平拉直，如图 5 所示。将两球由静止释放。在各自轨迹的最低点 ( 　　 ) 图 5 圆周运动问题 圆周运动问题 A. P 球的速度一定大于 Q 球的速度 B. P 球的动能一定小于 Q 球的动能 C. P 球所受绳的拉力一定大于 Q 球所受绳的拉力 D. P 球的向心加速度一定小于 Q 球的向心加速度 答案　 C 【典例 2 】 (2017· 全国卷 Ⅱ ， 17) 如图 6 ，半圆形光滑轨道固定在水平地面上，半圆的直径与地面垂直，一小物块以速度 v 从轨道下端滑入轨道，并从轨道上端水平飞出，小物块落地点到轨道下端的距离与轨道半径有关，此距离最大时，对应的轨道半径为 ( 重力加速度大小为 g )( 　　 ) 平抛运动与圆周运动的组合问题 图 6 物块做平抛运动时，落地点到轨道下端的距离 x ＝ v 1 t ， 答案　 B 1. ( 多选 ) 北京时间 2017 年 9 月 7 日，全运会在天津举办，山东队 28 岁的张成龙以 14.733 分在男子单杠决赛中获得第一名。假设张成龙训练时做 “ 单臂大回环 ” 的高难度动作时，用一只手抓住单杠，伸展身体，以单杠为轴做圆周运动。如图 7 甲所示，张成龙运动到最高点时，用力传感器测得张成龙与单杠间弹力大小为 F ，用速度传感器记录他在最高点的速度大小为 v ，得到 F － v 2 图象如图乙所示。 g 取 10 m/s 2 ，则下列说法中正确的是 ( 　　 ) 图 7 A. 张成龙的质量为 65 kg B. 张成龙的重心到单杠的距离为 0.9 m C. 当张成龙在最高点的速度为 4 m/s 时，张成龙受单杠的弹力方向向上 D. 在完成 “ 单臂大回环 ” 的过程中，张成龙运动到最低点时，单臂最少要承受 3 250 N 的 力 答案　 ABD 图 8 设小球 2 和小球 3 通过最高点时的速度分别为 v 2 ′ 和 v 3 ′ 。 小球 1 做的不是平抛运动，则小球 1 和小球 2 做平抛运动的时间之比不是 1 ∶ 1 ，故选项 B 、 D 正确， C 错误。 答案　 BD 【典例 1 】 (2018· 全国卷 Ⅲ ， 15) 为了探测引力波， “ 天琴计划 ” 预计发射地球卫星 P ，其轨道半径约为地球半径的 16 倍；另一地球卫星 Q 的轨道半径约为地球半径的 4 倍。 P 与 Q 的周期之比约为 ( 　　 ) A.2 ∶ 1 B.4 ∶ 1 C.8 ∶ 1 D.16 ∶ 1 万有引力定律与天体的运动 开普勒三定律与万有引力定律的应用 答案　 C 【典例 2 】 ( 多选 ) (2017· 全国卷 Ⅱ ， 19) 如图 9 ，海王星绕太阳沿椭圆轨道运动， P 为近日点， Q 为远日点， M 、 N 为轨道短轴的两个端点，运行的周期为 T 0 ，若只考虑海王星和太阳之间的相互作用，则海王星在从 P 经过 M 、 Q 到 N 的运动过程中 ( 　　 ) 图 9 答案　 CD 【典例 3 】 (2018· 全国卷 Ⅱ ， 16) 2018 年 2 月，我国 500 m 口径射电望远镜 ( 天眼 ) 发现毫秒脉冲星 “ J0318 ＋ 0253 ” ，其自转周期 T ＝ 5.19 ms 。假设星体为质量均匀分布的球体，已知万有引力常量为 6.67 × 10 － 11 N·m 2 /kg 2 。以周期 T 稳定自转的星体的密度最小值约为 ( 　　 ) A.5 × 10 9 kg/m 3 B.5 × 10 12 kg/m 3 C.5 × 10 15 kg/m 3 D.5 × 10 18 kg/m 3 天体质量、密度的估算 答案　 C 【典例 4 】 (2017· 全国卷 Ⅲ ， 14) 2017 年 4 月，我国成功发射的天舟一号货运飞船与天宫二号空间实验室完成了首次交会对接，对接形成的组合体仍沿天宫二号原来的轨道 ( 可视为圆轨道 ) 运行。与天宫二号单独运行时相比，组合体运行的 ( 　　 ) A . 周期变大 B . 速率变大 C . 动能变大 D . 向心加速度变 大 卫星运行参量的分析 答案　 C 【典例 5 】 ( 多选 ) (2013· 新课标全国卷 Ⅰ ， 20) 2012 年 6 月 18 日，神舟九号飞船与天宫一号目标飞行器在离地面 343 km 的近圆形轨道上成功进行了我国首次载人空间交会对接。对接轨道所处的空间存在极其稀薄的大气。下列说法正确的是 ( 　　 ) A . 为实现对接，两者运行速度的大小都应介于第一宇宙速度和第二宇宙速度之间 B . 如不加干预，在运行一段时间后，天宫一号的动能可能会增加 C . 如不加干预，天宫一号的轨道高度将缓慢降低 D . 航天员在天宫一号中处于失重状态，说明航天员不受地球引力作用 卫星的变轨与对接 答案　 BC 【典例 6 】 ( 多选 ) (2018· 全国卷 Ⅰ ， 20) 2017 年，人类第一次直接探测到来自双中子星合并的引力波。根据科学家们复原的过程，在两颗中子星合并前约 100 s 时，它们相距约 400 km ，绕二者连线上的某点每秒转动 12 圈。将两颗中子星都看作是质量均匀分布的球体，由这些数据、万有 引力 常量并利用牛顿力学知识，可以估算出这一时刻两颗中子星 ( 　　 ) A . 质量之积 B . 质量之和 C . 速率之和 D . 各自的自转角速度 天体运动中的双星、多星问题 答案　 BC 1 . 分析卫星轨道半径与运行参数关系应注意 卫 星轨道半径越大，同一卫星所受万有引力越小，其线速度、角速度、向心加速度越小，周期越大；动能越小，势能越大，机械能越大。 2 . 天体运动与几何关系相结合问题 ( 1) 多星模型中分析天体的运行轨道半径与星体间距的关系。 ( 2) 求解传播时间、挡光时间时通常需作出轨迹圆的切线，分析边角关系。 1. ( 多选 ) 导航系统是一种利用人造卫星对物体进行定位测速的工具，目前世界上比较完善的导航系统有美国的 GPS 系统，中国的北斗系统，欧洲的伽利略导航系统以及俄罗斯的 GLONASS 系统，其中美国的 GPS 系统采用的是运行周期为 12 小时的人造卫星，中国的北斗系统一部分采用了同步卫星，现有一颗北斗同步卫星 A 和一颗赤道平面上方的 GPS 卫星 B ，某时刻两者刚好均处在地面某点 C 的正上方，如图 10 所示，下列说法正确的是 ( 　　 ) A. A 的速度比 B 的小 B . 若两者质量相等，则发射 A 需要更多的能量 C . 此时刻 B 处在 A 、 C 连线的中点 D . 从此时刻起，经过 12 小时，两者相距最 远 图 10 答案　 ABD 2. ( 多选 ) 极地近地卫星运动的轨道平面通过地球的南北两极 ( 轨道可视为圆 ) ，如图 11 所示，关于极地近地卫星、地球同步卫星和赤道上的物体，下列说法正确的是 ( 　　 ) 图 11 A. 如果地球的自转变快，同步卫星的高度将变低 B. 如果地球的自转变快，极地近地卫星的速度将变小 C. 如果地球的自转变快，赤道上的重力加速度将变小 D. 若极地近地卫星、地球同步卫星和赤道上的物体的向心加速度分别为 a 1 、 a 2 、 a 3 ，则 a 1 ＞ a 2 ＞ a 3 答案　 ACD 3. ( 多选 ) 2017 年 4 月，我国第一艘货运飞船天舟一号顺利升空，随后与天宫二号对接。假设天舟一号从 B 点发射经过椭圆轨道运动到天宫二号所在的圆轨道上完成对接，如图 12 所示。已知天宫二号的轨道半径为 r ，天舟一号沿椭圆轨道运动的周期为 T ， A 、 B 两点分别为椭圆轨道的远地点和近地点，地球半径为 R ，引力常量为 G 。则下列说法正确的是 ( 　　 ) A . 天宫二号的运行速度小于 7.9 km/s B . 天舟一号的发射速度大于 11.2 km/s C . 根据题中信息可以求出地球的质量 D . 天舟一号在 A 点的运行速度大于天宫二号在 A 点的运行速 度 图 12 答案　 AC 竖直平面的圆周运动 “ 绳、杆 ” 模型 热点模型构建——常考的圆周运动模型 来源 图例 考向 模型核心归纳 2015· 新课标全国卷 Ⅰ 第 22 题 圆周运动、 超 重 、失重 1. 常考的模型 ( 1) 物体 运动满足 “ 绳 ” 模型特征，竖直圆轨道光滑 ( 2) 物体运动满足 “ 绳 ” 模型特征，竖直圆轨道粗 糙 (3) 物体运动满足 “ 杆 ” 模型特征，竖直圆轨道光滑 2016· 全国卷 Ⅱ 第 16 题 受力分析、牛顿第二定律、圆周运动、动能定理 来源 图例 考向 模型核心归纳 2016· 全国卷 Ⅱ 第 25 题 受力分析、机械能守恒定律、圆周运动、牛顿第二定律 ( 4) 物体运动满足 “ 杆 ” 模型特征，竖直圆轨道粗糙 (5) 两个物体沿竖直圆轨道做圆周运动 (6) 同一物体在不同的竖直圆轨道做圆周运动 (7) 物体在弹簧弹力、电场力或洛伦兹力共同作用下的圆周运 动 2016· 全国卷 Ⅲ 第 24 题 受力分析、圆周运动、机械能守恒定律、牛顿第二定律 来源 图例 考向 模型核心归纳 2017· 全国卷 Ⅱ 第 17 题 平抛运动、功能关系及极值的求解方法 2 . 模型解 法 2018· 全国卷 Ⅲ 第 25 题 圆周运动、动能定理、动量 【例】 如图 13 所示，水平路面 CD 的右侧有一长度 L 1 ＝ 2 m 的木板。一物块放在木板的最右端，并随木板一起向左侧固定的平台运动，木板的上表面与平台等高。平台上表面 AB 的长度 s ＝ 3 m ，光滑半圆轨道 AFE 竖直固定在平台上，圆轨道半径 R ＝ 0.4 m ，最低点与平台 AB 相切于 A 点。当木板的左端与平台的距离 L ＝ 2 m 时，木板与物块向左运动的速度 v 0 ＝ 8 m/s 。木板与平台的竖直壁碰撞后，木板立即停止运动，物块在木板上滑动并滑上平台。已知木板与路面间的动摩擦因数 μ 1 ＝ 0.05 ，物块与木板的上表面及轨道 AB 间的动摩擦因数均为 μ 2 ＝ 0.1 ，物块质量 m ＝ 1 kg ，取 g ＝ 10 m/s 2 。 图 13 (1) 求物块进入圆轨道时对轨道上的 A 点的压力； (2) 判断物块能否到达圆轨道的最高点 E 。如果能，求物块离开 E 点后在平台上的落点到 A 点的距离；如果不能，则说明理由。 教你建构物理模型 第一步：把握过程，构建运动模型 过程 1 DC 段 木板、物块共同向左减速运动 过程 2 木板与 BC 碰撞后 物块在木板上匀减速运动 过程 3 物块滑到 BA 上 物块在 BA 上匀减速运动 过程 4 光滑半圆轨道上 物块做圆周运动 过程 5 物块若能达 E 点，以 E 点飞出过程 可能从 E 点水平抛出 解析　 (1) 设木板质量为 M ，物块随板运动撞击竖直壁 BC 时的速度为 v 1 ，由动能定理得 由牛顿第三定律知，物块对轨道 A 点的压力大小为 140 N ，方向竖直向下。 解得 x ＝ 2.4 m 。 答案 　 (1)140 N ，方向竖直向下　 (2) 能　 2.4 m