高考卷 2006年普通高等学校招生全国统一考试 数学（天津卷 12页

2006 年普通高等学校招生全国统一考试（天津卷） 数学（理工类） 第Ⅰ卷（选择题 共 50 分） 一、选择题（本大题共 10 个小题，每小题 5 分，满分 50 分。在每小题给出的 四个选项中只有一个正确答案） 1、i 是虚数单位，  i i 1 （ ） A． i2 1 2 1  B． i2 1 2 1  C． i2 1 2 1  D． i2 1 2 1  2、如果双曲线的两个焦点分别为 )0,3(1 F 、 )0,3(2F ，一条渐近线方程为 xy 2 ，那 么它的两条准线间的距离是（ ） A． 36 B． 4 C． 2 D．1 3、设变量 x 、 y 满足约束条件       63 2 xy yx xy ，则目标函数 yxz  2 的最小值为（ ） A． 2 B．3 C． 4 D．9 4、设集合 }30|{  xxM ， }20|{  xxN ，那么“ Ma  ”是“ Na  ”的 （ ） A．充分而不必要条件 B．必要而不充分条件 C．充分必要条件 D．既不充分也不必要条件 5、将 4 个颜色互不相同的球全部放入编号为 1 和 2 的两个盒子里，使得放入每个盒子里 的球的个数不小于该盒子的编号，则不同的放球方法有（ ） A．10 种 B．20 种 C．36 种 D．52 种 6、设 m 、n 是两条不同的直线， 、  是两个不同的平面.考查下列命题，其中正确的命 题是（ ） A．   nmnm ,, B． nmnm   //,,// C． nmnm   //,, D．   nmnm,,  7、已知数列 }{ na 、 }{ nb 都是公差为 1 的等差数列，其首项分别为 1a 、 1b ，且 511  ba ， * 11, Nba  ．设 nbn ac  （ *Nn  ），则数列 }{ nc 的前 10 项和等于（ ） A．55 B．70 C．85 D．100 8、已知函数 xbxaxf cossin)(  （ a 、 b 为常数， 0a ， Rx  ）在 4 x 处取得 最小值，则函数 )4 3( xfy   是（ ） A．偶函数且它的图象关于点 )0,( 对称 B．偶函数且它的图象关于点 )0,2 3(  对称 C．奇函数且它的图象关于点 )0,2 3(  对称 D．奇函数且它的图象关于点 )0,( 对称 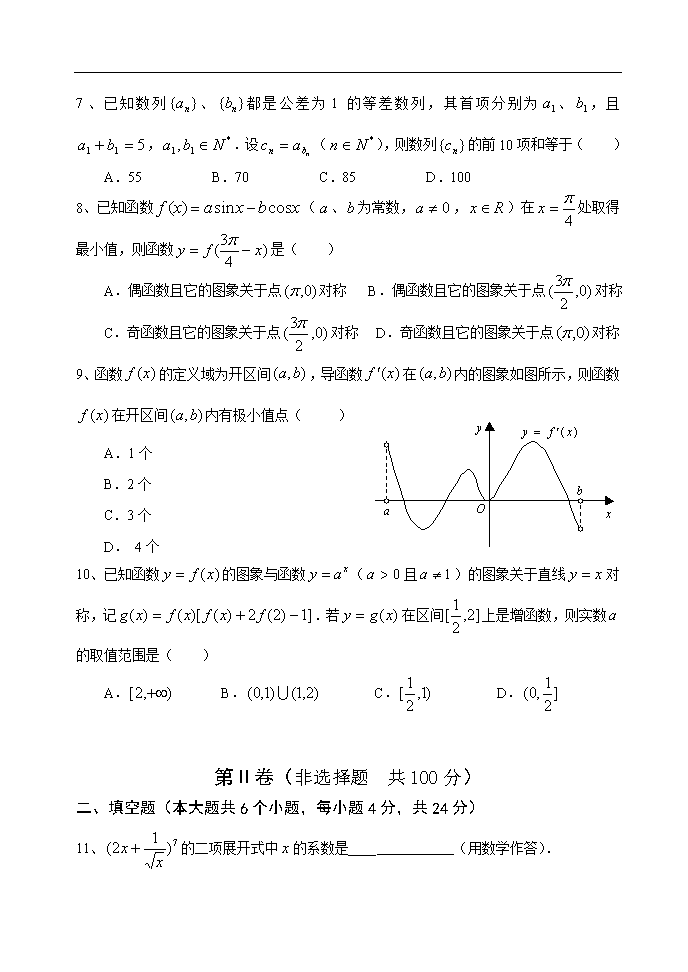9、函数 )(xf 的定义域为开区间 ),( ba ，导函数 )(xf  在 ),( ba 内的图象如图所示，则函数 )(xf 在开区间 ),( ba 内有极小值点（ ） A．1 个 B．2 个 C．3 个 D． 4 个 10、已知函数 )(xfy  的图象与函数 xay  （ 0a 且 1a ）的图象关于直线 xy  对 称，记 ]1)2(2)()[()(  fxfxfxg ．若 )(xgy  在区间 ]2,2 1[ 上是增函数，则实数 a 的取值范围是（ ） A． ),2[  B． )2,1()1,0(  C． )1,2 1[ D． ]2 1,0( 第Ⅱ卷（非选择题 共 100 分） 二、填空题（本大题共 6 个小题，每小题 4 分，共 24 分） 11、 7)12( x x  的二项展开式中 x 的系数是____ （用数学作答）． a b x y )(xfy  O a b x y )(xfy  O 12、设向量 a 与b  的夹角为 ，且 )3,3(a ， )1,1(2  ab  ，则 cos __________． 13、如图，在正三棱柱 111 CBAABC  中， 1AB ． 若二面角 1CABC  的大小为 60 ，则点C 到平面 1ABC 的距离为______________． 14、设直线 3 0ax y   与圆 2 2( 1) ( 2) 4x y    相交于 A 、 B 两点，且弦 AB 的长 为 2 3 ，则 a  ____________． 15、某公司一年购买某种货物 400 吨，每次都购买 x 吨，运费为 4 万元/次，一年的总存储 费用为 4x 万元，要使一年的总运费与总存储费用之和最小，则 x  吨． 16 、 设 函 数   1 1  xxf ， 点 0A 表 示 坐 标 原 点 ， 点    *, NnnfnAn  ， 若 向 量 0 1 1 2 1n n na A A A A A A        ， n 是 na  与 i 的 夹 角 ，（ 其 中  0,1i ）， 设 nnS  tantantan 21   ，则 nn S lim = ． 三、解答题（本题共 6 道大题，满分 76 分） 17、（本题满分 12 分） 如图，在 ABC 中， 2AC  ， 1BC  ， 4 3cos C ． （1）求 AB 的值； （2）求  CA 2sin 的值. 18、（本题满分 12 分） 某射手进行射击训练，假设每次射击击中目标的概率为 5 3 ，且各次射击的结果互不影响。 （1）求射手在 3 次射击中，至少有两次连续击中目标的概率（用数字作答）； （2）求射手第 3 次击中目标时，恰好射击了 4 次的概率（用数字作答）； （3）设随机变量 表示射手第 3 次击中目标时已射击的次数，求 的分布列． 19、（本题满分 12 分） 如图，在五面体 ABCDEF 中，点O 是矩形 ABCD 的对角线的交点，面CDE 是等边三角形，棱 // 1 2EF BC ． （1）证明 FO //平面CDE ； （2）设 3BC CD ，证明 EO  平面 CDF ． 班级_____________ 姓名___________________ 20、（本题满分 12 分） 已知函数    cos16 3cos34 23  xxxf ，其中 ,Rx  为参数，且  20  ． （1）当时 0cos  ，判断函数  xf 是否有极值； （2）要使函数  xf 的极小值大于零，求参数 的取值范围； （3）若对（2）中所求的取值范围内的任意参数 ，函数  xf 在区间 aa ,12  内都是增 函数，求实数 a 的取值范围． 21、（本题满分 14 分） 已知数列   nn yx , 满足 2,1 2121  yyxx ，并且 1 1 1 1 ,      n n n n n n n n y y y y x x x x  （  为非零参数， ,4,3,2n ）． （1）若 531 ,, xxx 成等比数列，求参数  的值； （2）当 0 时，证明  * 1 1 Nny x y x n n n n    ； 当 1 时，证明  * 1133 22 22 11 1 Nnyx yx yx yx yx yx nn nn        . 22、（本题满分 14 分） 如图，以椭圆  012 2 2 2  ba b y a x 的中心 O 为 圆心，分别以 a 和b 为半径作大圆和小圆。过椭圆右焦 点   bccF 0, 作垂直于 x 轴的直线交大圆于第一象 限内的点 A ．连结OA 交小圆于点 B ．设直线 BF 是小 圆的切线． （1）证明 abc 2 ，并求直线 BF 与 y 轴的交点 M 的 坐标； （ 2 ） 设 直 线 BF 交 椭 圆 于 P 、 Q 两 点 ， 证 明 21 2OP OQ b   ． 参考答案： 一、选择题 题号 1 2 3 4 5 6 7 8 9 10 答案 A C B B A B C D A D 二、填空题 11、280 12、 3 10 10 13、 3 4 14、0 15、20 16、1 1、i 是虚数单位，  i i 1 (1 ) 1 2 2 2 i i i   ，选 A. 2、如果双曲线的两个焦点分别为 )0,3(1 F 、 )0,3(2F ，一条渐近线方程为 xy 2 ，∴ 2 2 9 2 a b b a     ，解得 2 2 3 6 a b     ，所以它的两条准线间的距离是 2 2 2a c   ， 选 C. 3、设变量 x 、y 满足约束条件 2 , 3 6 y x x y y x        在坐标系中画出可行域△ABC，A(2，0)，B(1， 1)，C(3，3)，则目标函数 2z x y  的最小值为 3，选 B. 4、设集合 }30|{  xxM ， }20|{  xxN ，M N ，所以若“ Ma  ”推不出 “ Na  ”；若“ Na  ”，则“ Ma  ”，所以“ Ma  ”是“ Na  ”的必要而不充分条件，选 B. 5、将 4 个颜色互不相同的球全部放入编号为 1 和 2 的两个盒子里，使得放入每个盒子里 的球的个数不小于该盒子的编号，分情况讨论：①1 号盒子中放 1 个球，其余 3 个放入 2 号盒子，有 1 4 4C  种方法；②1 号盒子中放 2 个球，其余 2 个放入 2 号盒子，有 2 4 6C  种 方法；则不同的放球方法有 10 种，选 A． 6、设 m 、 n 是两条不同的直线， 、  是两个不同的平面。下列命题中正确的命题是 nmnm   //,,// ，选 B. 7、已知数列 }{ na 、 }{ nb 都是公差为 1 的等差数列，其首项分别为 1a 、 1b ，且 511  ba ， * 11, Nba  ． 设 nbn ac  （ *Nn  ）， 则 数 列 }{ nc 的 前 10 项 和 等 于 1 2 10b b ba a a   = 1 1 11 9b b ba a a    ， 1 1 1( 1) 4ba a b    ， ∴ 1 1 11 9b b ba a a    = 4 5 6 13 85     ，选 C. 8 、 已 知 函 数 ( ) sin cosf x a x b x  (a 、 b 为 常 数 , 0, )a x R  ， ∴ 2 2( ) sin( )f x a b x    的 周 期 为 2π ， 若 函 数 在 4 x 处 取 得 最 小 值 ， 不 妨 设 3( ) sin( )4f x x   ， 则 函 数 3( )4y f x  = 3 3sin( ) sin4 4x x    ， 所 以 3( )4y f x  是奇函数且它的图象关于点 ( ,0) 对 称，选 D. a b x y )(xfy  O a b x y )(xfy  O 9、函数 )(xf 的定义域为开区间 ),( ba ，导函数 )(xf  在 ),( ba 内的图象如图所示，函数 )(xf 在开区间 ),( ba 内有极小值的点即函数由减函数变为增函数的点，其导数值为由负到 正的点，只有 1 个，选 A. 10、已知函数 )(xfy  的图象与函数 xay  （ 0a 且 1a ）的图象关于直线 xy  对 称,则 ( ) logaf x x ，记 ( ) ( )[ ( ) (2) 1]g x f x f x f   = 2(log ) (log 2 1)loga a ax x  ．当 a>1 时，若 )(xgy  在区间 ]2,2 1[ 上是增函数， logay x 为增函数，令 logat x ，t∈ [ 1log 2a , log 2a ]，要求对称轴 log 2 1 1log2 2 a a  ≤ ，矛盾；当 0