- 104.50 KB
- 2021-05-25 发布
课题:反比例函数的图象与性质(1)
教学目标:
使学生会作反比例函数的图象,并能理解反比例函数的性质。培养提高学生的计算能力和作图能力。
教学重点、难点:
重点:作反比例函数的图象
难点:理解反比例函数的性质。
教学过程:
一、复习:
1、函数有哪几种表示方法?
答:图象法、解析法、列表法
2、一次函数y=kx+b有什么性质?
答:一次函数y=kx+1的图象是一条直线。
当k>0时,y随x的增大而增大;当k<0时,y随x的增大而减小。
二、新授:
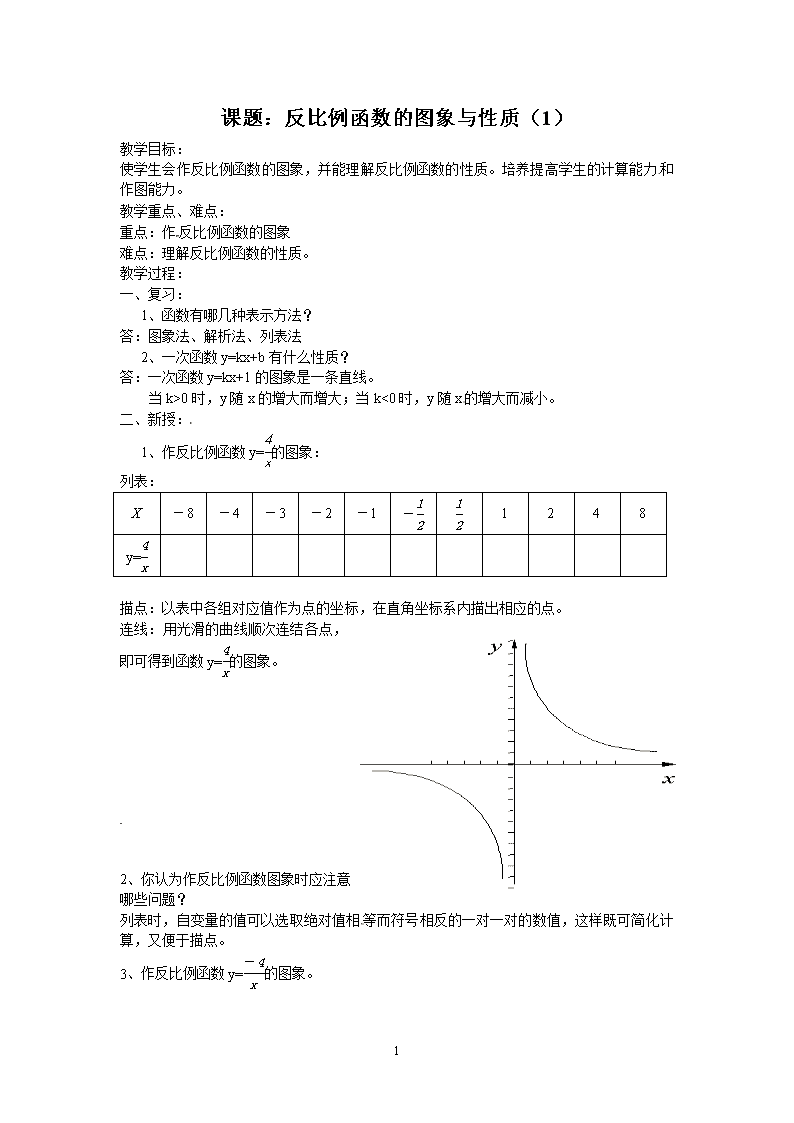
1、作反比例函数y=的图象:
列表:
X
-8
-4
-3
-2
-1
-
1
2
4
8
y=
描点:以表中各组对应值作为点的坐标,在直角坐标系内描出相应的点。
连线:用光滑的曲线顺次连结各点,即可得到函数y=的图象。
2、你认为作反比例函数图象时应注意哪些问题?
列表时,自变量的值可以选取绝对值相等而符号相反的一对一对的数值,这样既可简化计算,又便于描点。
3、作反比例函数y=的图象。
2
4、观察函数y=和y=的图象,它们有什么相同点和不同点?
图象分别都是由两支曲线组成的,它们都不与坐标轴相交,两个函数图象都是轴对称图形,它们各自都有两条对称轴。
5、反比例函数y=的图象是由两支曲线组成的,当k>0时,两支曲线分别位于一、三象限内,当k<0 时,两支曲线分别位于第二、四象限内。
三、随堂练习
P82:1、2
3.分别在坐标系中画出它们的函数图象。
(1)y= (2)y=
4.已知x,y满足xy=-4,用x的代数式表示y,并画出函数图象.
5.反比例函数的图象经过点(-2,4),求它的解析式,并画出函数图象,图象分布在哪几个象限?与坐标轴的交点是什么?
6.已知三角形的面积为24c,任一边a(cm)与这边上的高h(cm)之间的函数关系式, 并写出自变量的取值范围,画出图象.
四、作业:
见作业纸
2