人教版八年级数学下册-第十七章检测题 5页

第十七章检测题 (时间：120 分钟满分：120 分) 一、选择题(每小题 3 分，共 30 分) 1．已知 Rt△ABC 的三边长分别为 a，b，c，且∠C＝90°，c＝37，a＝12，则 b 的值 为 B A．50B．35C．34D．26 2．由下列线段 a，b，c 不能组成直角三角形的是 D A．a＝1，b＝2，c＝ 3B．a＝1，b＝2，c＝ 5 C．a＝3，b＝4，c＝5D．a＝2，b＝2 3，c＝3 3．在 Rt△ABC 中，∠C＝90°，AC＝9，BC＝12，则点 C 到 AB 的距离是 A A．36 5 B．12 25C．9 4D．3 3 4 4．已知三角形三边长为 a，b，c，如果 a－6＋|b－8|＋(c－10)2＝0，则△ABC 是 C A．以 a 为斜边的直角三角形 B．以 b 为斜边的直角三角形 C．以 c 为斜边的直角三角形 D．不是直角三角形 5．(2019·咸宁)勾股定理是“人类最伟大的十个科学发现之一”．我国对勾股定理的证 明是由汉代的赵爽在注解《周髀算经》时给出的，他用来证明勾股定理的图案被称为“赵爽 弦图”.2002 年在北京召开的国际数学大会选它作为会徽．下列图案中是“赵爽弦图”的是 B 6．设 a，b 是直角三角形的两条直角边，若该三角形的周长为 6，斜边长为 2.5，则 ab 的值是 D A．1.5B．2C．2.5D．3 7．如图，在 Rt△ABC 中，∠A＝30°，DE 垂直平分斜边 AC 交 AB 于点 D，E 是垂足， 连接 CD，若 BD＝1，则 AC 的长是 A A．2 3B．2C．4 3D．4 第 7 题图 第 9 题图 第 10 题图 8．一木工师傅测量一个等腰三角形的腰、底边和底边上的高的长，但他把这三个数据 与其他数据弄混了，请你帮他找出来，应该是 C A．13，12，12B．12，12，8C．13，10，12D．5，8，4 9．如图，小亮将升旗的绳子拉到旗杆底端，绳子末端刚好接触到地面，然后将绳子末 端拉到距离旗杆 8m 处，发现此时绳子末端距离地面 2m，则旗杆的高度为(滑轮上方的部分 忽略不计)D A．12mB．13mC．16mD．17m 10．如图，在平面直角坐标系中，Rt△OAB 的顶点 A 在 x 轴的正半轴上，顶点 B 的坐 标为(3， 3)，点 C 的坐标为(1 2 ，0)，点 P 为斜边 OB 上的一个动点，则 PA＋PC 的最小值为 B A． 13 2 B． 31 2 C．3＋ 19 2 D．2 7 二、填空题(每小题 3 分，共 15 分) 11．把命题“对顶角相等”的逆命题改写成“如果…那么…”的形式：如果两个角相等， 那么它们是对顶角． 12．(2019·常州)平面直角坐标系中，点 P(－3，4)到原点的距离是 5． 13．如图，阴影部分是两个正方形，其他三个图形是一个正方形和两个直角三角形，则 阴影部分的面积之和为 64． 14．(2019·东营)已知等腰三角形的底角是 30°，腰长为 2 3，则它的周长是 6＋4 3． 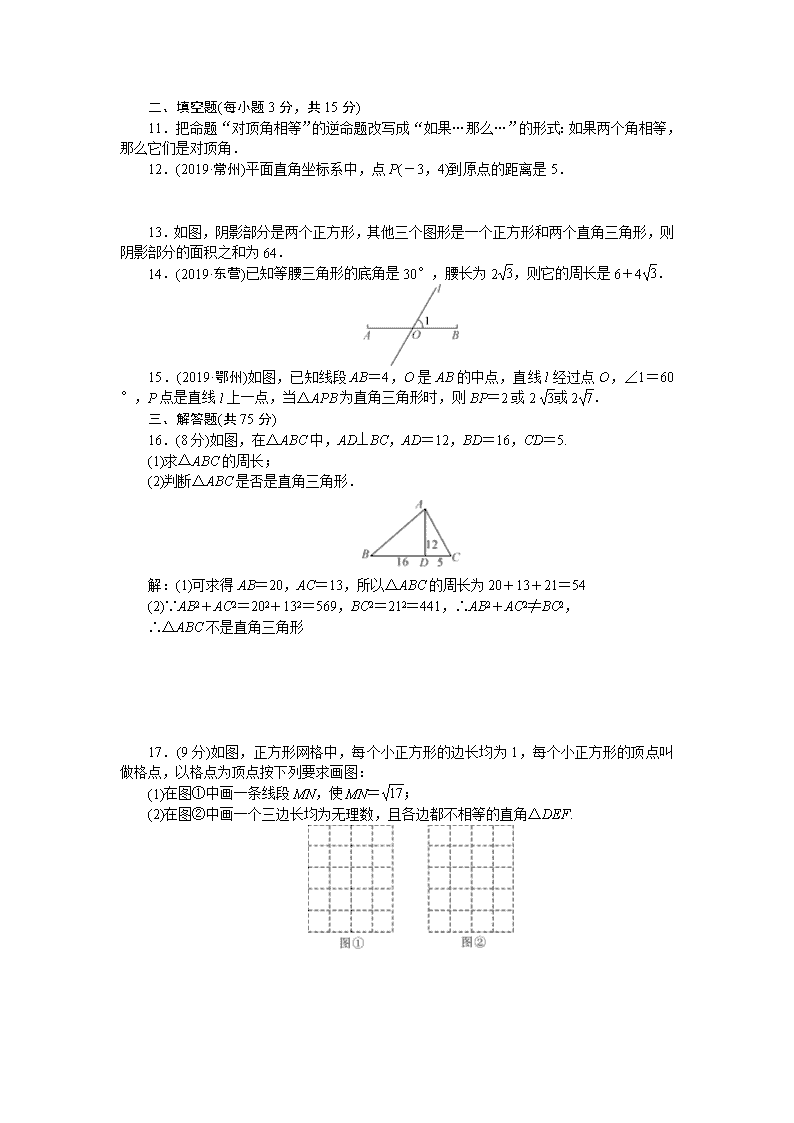15．(2019·鄂州)如图，已知线段 AB＝4，O 是 AB 的中点，直线 l 经过点 O，∠1＝60 °，P 点是直线 l 上一点，当△APB 为直角三角形时，则 BP＝2 或 2 3或 2 7． 三、解答题(共 75 分) 16．(8 分)如图，在△ABC 中，AD⊥BC，AD＝12，BD＝16，CD＝5. (1)求△ABC 的周长； (2)判断△ABC 是否是直角三角形． 解：(1)可求得 AB＝20，AC＝13，所以△ABC 的周长为 20＋13＋21＝54 (2)∵AB2＋AC2＝202＋132＝569，BC2＝212＝441，∴AB2＋AC2≠BC2， ∴△ABC 不是直角三角形 17．(9 分)如图，正方形网格中，每个小正方形的边长均为 1，每个小正方形的顶点叫 做格点，以格点为顶点按下列要求画图： (1)在图①中画一条线段 MN，使 MN＝ 17； (2)在图②中画一个三边长均为无理数，且各边都不相等的直角△DEF. 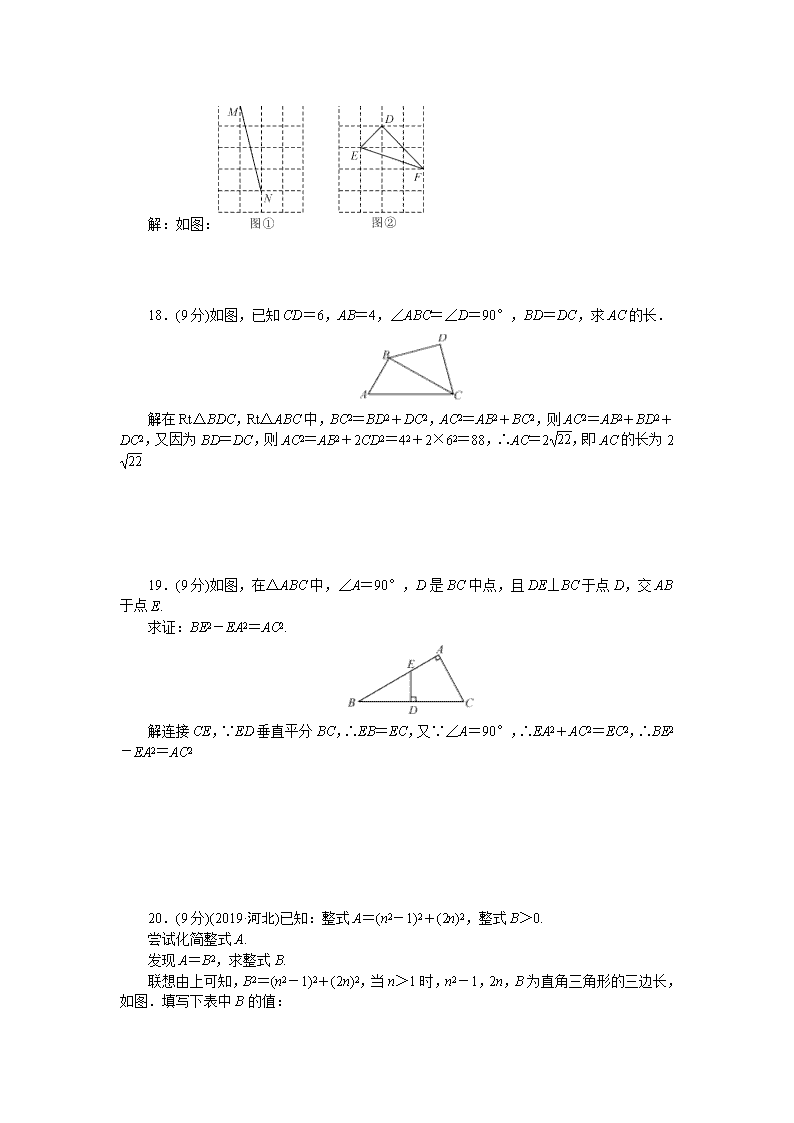解：如图： 18．(9 分)如图，已知 CD＝6，AB＝4，∠ABC＝∠D＝90°，BD＝DC，求 AC 的长． 解：在 Rt△BDC，Rt△ABC 中，BC2＝BD2＋DC2，AC2＝AB2＋BC2，则 AC2＝AB2＋BD2 ＋DC2，又因为 BD＝DC，则 AC2＝AB2＋2CD2＝42＋2×62＝88，∴AC＝2 22，即 AC 的长 为 2 22 19．(9 分)如图，在△ABC 中，∠A＝90°，D 是 BC 中点，且 DE⊥BC 于点 D，交 AB 于点 E. 求证：BE2－EA2＝AC2. 解：连接 CE，∵ED 垂直平分 BC，∴EB＝EC，又∵∠A＝90°，∴EA2＋AC2＝EC2， ∴BE2－EA2＝AC2 20．(9 分)(2019·河北)已知：整式 A＝(n2－1)2＋(2n)2，整式 B＞0. 尝试化简整式 A. 发现 A＝B2，求整式 B. 联想由上可知，B2＝(n2－1)2＋(2n)2，当 n＞1 时，n2－1，2n，B 为直角三角形的三边长， 如图．填写下表中 B 的值： 直角三角形三边 n2－1 2n B 勾股数组Ⅰ / 8 勾股数组Ⅱ 35 / 解：A＝(n2－1)2＋(2n)2＝n4－2n2＋1＋4n2＝n4＋2n2＋1＝(n2＋1)2，∵A＝B2，B＞0，∴ B＝n2＋1，当 2n＝8 时，n＝4，∴n2＋1＝42＋1＝17；当 n2－1＝35 时，n2＋1＝37.故答案为： 17；37 21．(10 分)如图，已知某学校 A 与直线公路 BD 的距离 AB 为 3000 米，且与该公路上 的一个车站 D 相距 5000 米，现要在公路边建一个超市 C，使之与学校 A 及车站 D 的距离相 等，那么该超市与车站 D 的距离是多少米？ 解：设超市 C 与车站 D 的距离是 x 米，则 AC＝CD＝x 米，BC＝(BD－x)米，在 Rt△ABD 中，BD＝ AD2－AB2＝4000 米，所以 BC＝(4000－x)米，在 Rt△ABC 中，AC2＝AB2＋BC2， 即 x2＝30002＋(4000－x)2，解得 x＝3125，因此该超市与车站 D 的距离是 3125 米 22．(10 分)一块长方体木块的各棱长如图所示，一只蜘蛛在木块的一个顶点 A 处，一只 苍蝇在这个长方体上和蜘蛛相对的顶点 B 处，蜘蛛急于捉住苍蝇，沿着长方体的表面向上 爬． (1)如果 D 是棱的中点，蜘蛛沿“AD→DB”路线爬行，它从 A 点爬到 B 点所走的路程 为多少？ (2)你认为“AD→DB”是最短路线吗？如果你认为不是，请计算出最短的路程． 解：(1)从点 A 爬到点 B 所走的路程为 AD＋BD＝ 42＋32＋ 22＋32＝(5＋ 13)cm (2) 不是，分三种情况讨论：①将下面和右面展到一个平面内，AB＝ （4＋6）2＋22＝ 104＝ 2 26(cm)；②将前面与右面展到一个平面内，AB＝ （4＋2）2＋62＝ 72＝6 2(cm)；③将 前面与上面展到一个平面内，AB＝ （6＋2）2＋42＝ 80＝4 5(cm)，∵6 2＜4 5＜2 26， ∴蜘蛛从 A 点爬到 B 点所走的最短路程为 6 2cm 23．(11 分)如图，已知正方形 OABC 的边长为 2，顶点 A，C 分别在 x 轴的负半轴和 y 轴的正半轴上，M 是 BC 的中点，P(0，m)是线段 OC 上一动点(C 点除外)，直线 PM 交 AB 的延长线于点 D. (1)求点 D 的坐标(用含 m 的代数式表示)； (2)当△APD 是以 AP 为腰的等腰三角形时，求 m 的值； 解：(1)先证△DBM≌△PCM，从中可得 BD＝PC＝2－m，则 AD＝2－m＋2＝4－m，∴ 点 D 的坐标为(－2，4－m) (2)分两种情况：①当 AP＝AD 时，AP2＝AD2，∴22＋m2＝(4－ m)2，解得 m＝3 2 ；②当 AP＝PD 时，过点 P 作 PH⊥AD 于点 H，∴AH＝1 2AD，∵AH＝OP， ∴OP＝1 2AD，∴m＝1 2(4－m)，∴m＝4 3 ，综上可得，m 的值为3 2 或4 3