2018届二轮复习7-3合情推理与演绎推理课件（全国通用） 34页

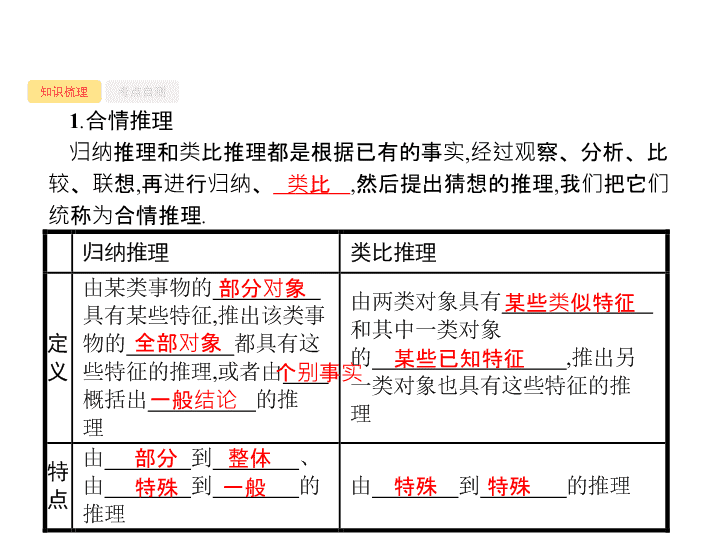
7 . 3 　 合情推理与演绎推理 - 2 - - 3 - 知识梳理 考点自测 1 . 合情推理 归纳推理和类比推理都是根据已有的事实 , 经过观察、分析、比较、联想 , 再进行归纳、 　 　 , 然后提出猜想的推理 , 我们把它们统称为合情推理 .   类比 部分对象 全部对象 个别事实 一般结论 某些类似特征 某些已知特征 部分 　 整体 特殊 　 一般 特殊 　 特殊 - 4 - 知识梳理 考点自测 - 5 - 知识梳理 考点自测 2 . 演绎推理 (1) 定义 : 从一般性的原理出发 , 推出某个特殊情况下的结论 , 我们把这种推理称为演绎推理 . (2) 特点 : 演绎推理是由一般到特殊的推理 . (3) 模式 :“ 三段论 ” 是演绎推理的一般模式 : 条件 特殊问题 M 是 P S 是 M - 6 - 知识梳理 考点自测 - 7 - 知识梳理 考点自测 1 . 判断下列结论是否正确 , 正确的画 “ √ ”, 错误的画 “ × ” . (1) 归纳推理得到的结论不一定正确 , 类比推理得到的结论一定正确 . ( 　　 ) (2) 归纳推理与类比推理都是由特殊到一般的推理 . ( 　　 ) (3) 在类比时 , 平面中的三角形与空间中的平行六面体作为类比对象较为合适 . ( 　　 ) (4) 演绎推理是由特殊到一般再到特殊的推理 . ( 　　 ) (5) 演绎推理在大前提、小前提和推理形式都正确时 , 得到的结论一定正确 . ( 　　 ) × × × × √ - 8 - 知识梳理 考点自测 2 . (2017 安徽滁州模拟 ) 若大前提是 : 任何实数的平方都大于 0, 小前提是 : a ∈ R , 结论是 : a 2 > 0, 则这个演绎推理出错在 ( 　　 ) A. 大前提 B. 小前提 C. 推理过程 D. 没有出错 A 解析 : 本题中大前提是错误的 , 因为 0 的平方不大于 0, 故选 A . - 9 - 知识梳理 考点自测 3 . ( 教材习题改编 P 7 T 1 ) 如图 , 根据图中的数构成的规律 , a 表示的数是 ( 　　 ) 1 2 　 2 3 　 4 　 3 4 　 12 　 12 　 4 5 　 48 　 a 　 48 　 5 A.12 B.48 C.60 D.144 D 解析 : 由题干图中的数据可知 , 每行除首末两数外 , 其他数等于其上一行两肩上的数字的乘积 . 所以 a= 12 × 12 = 144 . - 10 - 知识梳理 考点自测 4 . (2017 全国 Ⅱ , 文 9) 甲、乙、丙、丁四位同学一起去向老师询问成语竞赛的成绩 . 老师说 : 你们四人中有 2 位优秀 ,2 位良好 , 我现在给甲看乙、丙的成绩 , 给乙看丙的成绩 , 给丁看甲的成绩 , 看后甲对大家说 : 我还是不知道我的成绩 . 根据以上信息 , 则 ( 　　 ) A. 乙可以知道四人的成绩 B. 丁可以知道四人的成绩 C. 乙、丁可以知道对方的成绩 D. 乙、丁可以知道自己的成绩 D 解析 : 由甲的说法知乙、丙一位优秀一位良好 . 则甲、丁也是一位优秀一位良好 ; 乙看到丙的成绩则知道自己的成绩 . 又丁看到甲的成绩 , 所以丁也知道自己的成绩 , 故选 D . - 11 - 知识梳理 考点自测 5 . ( 教材习题改编 P 7 T 2 ) 在平面上 , 若两个正三角形的边长的比为 1 ∶ 2, 则它们的面积比为 1 ∶ 4 . 类似地 , 在空间中 , 若两个正四面体的棱长的比为 1 ∶ 2, 则它们的体积比为 　　　　　 .   1 ∶ 8 解析 : 由平面图形的面积类比立体图形的体积得出 : 在空间内 , 若两个正四面体的棱长的比为 1 ∶ 2, 则它们的底面积之比为 1 ∶ 4, 对应高之比为 1 ∶ 2, 所以体积比为 1 ∶ 8 . - 12 - 考点一 考点二 考点三 考点四 归纳推理 ( 多考向 ) 考向 1 　 数的归纳 例 1 观察下列各式 :5 5 = 3 125,5 6 = 15 625,5 7 = 78 125, … , 则 5 2 016 的末四位数字为 ( 　　 ) A.3 125 B.5 625 C.0 625 D.8 125 C 解析 : 5 8 = 390 625,5 9 = 1 953 125, … , 由此看出 , 末四位数字具有周期性 , 且周期为 4, 又 2 016 = 4 × 504, 由此知 5 2 016 的末四位数字应为 0625, 故选 C . 思考 进行数的归纳时 , 应注意观察数的什么变化 ? - 13 - 考点一 考点二 考点三 考点四 考向 2 　 式的归纳 …… 根据以上事实 , 由归纳推理可得 : 当 n ∈ N * 且 n ≥ 2 时 , f n ( x ) =f ( f n- 1 ( x )) = 　　　　　 .   - 14 - 考点一 考点二 考点三 考点四 思考 进行式的归纳时 , 应注意寻找什么 ? - 15 - 考点一 考点二 考点三 考点四 考向 3 　 形的归纳 例 3 仔细观察下面 4 个数字所表示的图形 :   请问 : 数字 100 所代表的图形中小方格的个数为 　　　　　 . 20 201 解析 : 观察所给图形知 , 数字 i+ 1 所代表的图形比数字 i 所代表的图形多 4( i+ 1) 个小方格 . 因此数字 100 所代表的图形中小方格的个数为 1 + 1 × 4 + 2 × 4 + 3 × 4 + … + 100 × 4 = 20 201 . 思考 进行形的归纳时 , 主要归纳什么的变化 ? - 16 - 考点一 考点二 考点三 考点四 解题心得 归纳推理的三个类型 1 . 数的归纳包括数字归纳和等式、不等式的归纳 , 解决此类问题时 , 需要细心观察 , 寻找数字变化与项数的关系或数字变化的周期性 . 2 . 式的归纳可根据已知或所求的式子寻找每个式子都具有的规律 . 3 . 形的归纳主要包括图形数目归纳和图形变化规律归纳 . - 17 - 考点一 考点二 考点三 考点四 对点训练 1 (1) 观察下列特殊的不等式 : - 18 - 考点一 考点二 考点三 考点四 (2) 观察下列各式 : a+b= 1, a 2 +b 2 = 3, a 3 +b 3 = 4, a 4 +b 4 = 7, a 5 +b 5 = 11, … , 则 a 8 +b 8 = 　　　　　 .   (3) 用火柴棒摆 “ 金鱼 ”, 如图所示 :   按照上面的规律 , 第 n 条 “ 金鱼 ” 需要火柴棒的根数为 　　　　　 .   47 6 n+ 2 - 19 - 考点一 考点二 考点三 考点四 - 20 - 考点一 考点二 考点三 考点四 (2) 通过观察发现 , 从第三项起 , 等式右边的常数分别为其前两项等式右边的常数的和 . 因此 , a 6 +b 6 = 11 + 7 = 18, a 7 +b 7 = 18 + 11 = 29, a 8 +b 8 = 29 + 18 = 47, 故答案为 47 . (3) 由图形间的关系可以看出 , 第一个图中有 8 根火柴棒 , 第二个图中有 8 + 6 根火柴棒 , 第三个图中有 8 + 2 × 6 根火柴棒 , 以此类推第 n 个 “ 金鱼 ” 需要火柴棒的根数是 8 + 6( n- 1), 即 6 n+ 2 . - 21 - 考点一 考点二 考点三 考点四 类比推理 - 22 - 考点一 考点二 考点三 考点四 思考 类比推理的关键是什么 ? 解题心得 类比推理的关键及类型 1 . 进行类比推理 , 应从具体问题出发 , 通过观察、分析、联想进行对比 , 提出猜想 . 其中找到合适的类比对象是解题的关键 . 2 . 类比推理常见的情形有 : 平面与空间类比 ; 低维与高维的类比 ; 等差与等比数列类比 ; 运算类比 ( 加与积 , 乘与乘方 , 减与除 , 除与开方 ); 数的运算与向量运算类比 ; 圆锥曲线间的类比等 . - 23 - 考点一 考点二 考点三 考点四 - 24 - 考点一 考点二 考点三 考点四 - 25 - 考点一 考点二 考点三 考点四 演绎推理 例 5 下面四个推导过程符合演绎推理三段论形式且推理正确的是 ( 　　 ) A. 大前提 : 无限不循环小数是无理数 ; 小前提 : π 是无理数 ; 结论 : π 是无限不循环小数 B. 大前提 : 无限不循环小数是无理数 ; 小前提 : π 是无限不循环小数 ; 结论 : π 是无理数 C. 大前提 : π 是无限不循环小数 ; 小前提 : 无限不循环小数是无理数 ; 结论 : π 是无理数 D. 大前提 : π 是无限不循环小数 ; 小前提 : π 是无理数 ; 结论 : 无限不循环小数是无理数 B 解析 : A 中小前提不是大前提的特殊情况 , 不符合三段论的推理形式 , 故 A 错 ;C,D 都不是由一般性命题到特殊性命题的推理 , 所以 A,C,D 都不正确 , 只有 B 正确 , 故选 B . - 26 - 考点一 考点二 考点三 考点四 思考 演绎推理中得出的结论一定正确吗 ? 解题心得 演绎推理的前提和结论之间有着某种蕴含关系 , 解题时要找准正确的大前提 . 一般地 , 若大前提不明确时 , 一般可找一个使结论成立的充分条件作为大前提 , 只要大前提、小前提和推理形式是正确的 , 结论必定是正确的 . - 27 - 考点一 考点二 考点三 考点四 对点训练 3 已知函数 y=f ( x ) 满足 : 对任意 a , b ∈ R , a ≠ b , 都有 af ( a ) +bf ( b ) >af ( b ) +bf ( a ), (1) 试证明 : f ( x ) 为 R 上的单调增函数 ; (2) 若 x , y 为正实数且 , 比较 f ( x+y ) 与 f (6) 的大小 . - 28 - 考点一 考点二 考点三 考点四 (1) 证明 设 x 1 , x 2 ∈ R , 且 x 1 x 1 f ( x 2 ) +x 2 f ( x 1 ), 所以 x 1 [ f ( x 1 ) -f ( x 2 )] +x 2 [ f ( x 2 ) -f ( x 1 )] > 0,[ f ( x 2 ) -f ( x 1 )]( x 2 -x 1 ) > 0 . 因为 x 1 0, 所以 f ( x 2 ) >f ( x 1 ) . 所以 y=f ( x ) 为 R 上的单调增函数 . - 29 - 考点一 考点二 考点三 考点四 生活中的合情推理 例 6 (2017 北京 , 文 14) 某学习小组由学生和教师组成 , 人员构成同时满足以下三个条件 : ( ⅰ ) 男学生人数多于女学生人数 ; ( ⅱ ) 女学生人数多于教师人数 ; ( ⅲ ) 教师人数的两倍多于男学生人数 . ① 若教师人数为 4, 则女学生人数的最大值为 　　　　　 ;   ② 该小组人数的最小值为 　　　　　 . 6 12 - 30 - 考点一 考点二 考点三 考点四 解析 : 设男学生人数为 x , 女学生人数为 y , 教师人数为 z , 则有 2 z>x>y>z , x , y , z ∈ N * . ① 教师人数为 4, 即 z= 4,8 >x>y> 4, 所以 y 的最大值为 6, 故女学生人数的最大值为 6 . ② 由题意知 2 z>x>y>z , x , y , z ∈ N * . 当 z= 1 时 ,2 >x>y> 1, x , y 不存在 ; 当 z= 2 时 ,4 >x>y> 2, x , y 不存在 ; 当 z= 3 时 ,6 >x>y> 3, x= 5, y= 4, 此时该小组人数最小 , 最小值为 5 + 4 + 3 = 12 . - 31 - 考点一 考点二 考点三 考点四 思考 如何解决生活中的合情推理问题 ? 解题心得 在进行合情推理时 , 要依据一定的 “ 规则 ”—— 已知条件、公式、法则、推理等 ; 只有不断地观察、比较、分析、推理 , 才能得到正确的答案 . - 32 - 考点一 考点二 考点三 考点四 对点训练 4 学生的语文、数学成绩均被评定三个等级 , 依次为 “ 优秀 ”“ 合格 ”“ 不合格 ” . 若学生甲的语文、数学成绩都不低于学生乙 , 且其中至少有一门成绩高于乙 , 则称 “ 学生甲比学生乙成绩好 ” . 如果一组学生中没有哪位学生比另一位学生成绩好 , 并且不存在语文成绩相同、数学成绩也相同的两位学生 , 那么这组学生最多有 ( 　　 ) A.2 人 B.3 人 C.4 人 D.5 人 B 解析 : 学生甲比学生乙成绩好 , 即学生甲两门成绩中一门高过学生乙 , 另一门不低于学生乙 . 一组学生中没有哪位学生比另一位学生成绩好 , 并且没有相同的成绩 , 则存在的情况是 , 最多有 3 人 , 其中一个语文最好 , 数学最差 ; 另一个语文最差 , 数学最好 ; 第三个人成绩均为中等 . 故选 B . - 33 - 考点一 考点二 考点三 考点四 1 . 合情推理与演绎推理的区别 (1) 归纳推理是由特殊到一般的推理 ; (2) 类比推理是由特殊到特殊的推理 ; (3) 演绎推理是由一般到特殊的推理 ; (4) 从推理的结论来看 , 合情推理的结论不一定正确 , 有待证明 ; 而演绎推理若大前提、小前提和推理形式正确 , 得到的结论一定正确 . 2 . 在数学研究中 , 在得到一个新结论前 , 合情推理能帮助猜测和发现结论 . 在证明一个数学结论之前 , 合情推理常常能为证明提供思路与方向 . 数学结论的证明主要通过演绎推理来进行 . 3 . “ 三段论 ” 式的演绎推理一定要保证大前提正确 , 且小前提是大前提的子集关系 , 这样经过正确推理 , 才能得出正确结论 . - 34 - 考点一 考点二 考点三 考点四 1 . 演绎推理常用来证明和推理数学问题 , 注意推理过程的严密性 , 书写格式的规范性 . 2 . 合情推理中运用猜想时不能凭空想象 , 要有猜想或拓展依据 .