- 342.30 KB
- 2021-05-24 发布
2.5直线与圆的位置关系(4)
同学们玩过空竹和悠悠球吗?在空竹和悠悠球的旋转的那一
瞬间,你能从中抽象出什么样数学图形?
【导入新课】
P
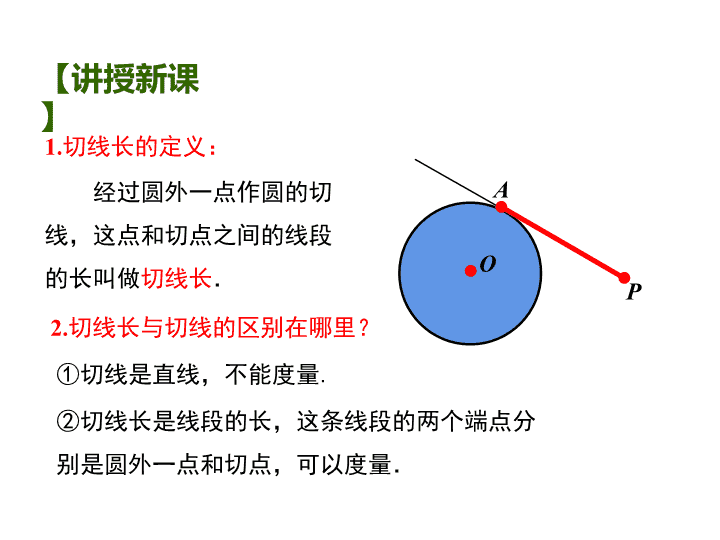
1.切线长的定义:
经过圆外一点作圆的切
线,这点和切点之间的线段
的长叫做切线长.
A
O
①切线是直线,不能度量.
②切线长是线段的长,这条线段的两个端点分
别是圆外一点和切点,可以度量.
2.切线长与切线的区别在哪里?
【讲授新课】
思考:PA为☉O的一条切线,沿着直线PO对折,设圆上与点
A重合的点为B.
Ø OB是☉O的一条半径吗?
Ø PB是☉O的切线吗?
(利用图形轴对称性解释)
Ø PA、PB有何关系?
Ø ∠APO和∠BPO有何关系?
O. P
A
B
PO
切线长定理:
过圆外一点所画的圆的
两条切线长相等.
PA、PB分别切☉O于A、B
PA = PB
∠OPA=∠OPB
几何语言:
切线长定理为证明线段相等、角相等提供了新的方法.注意
O. P
A
B
已知,如图PA、PB是☉O的两条
切线,A、B为切点.
求证:PA=PB,∠APO=∠BPO.
做一做
证明:∵PA切☉O于点A,
∴ OA⊥PA.
同理可得OB⊥PB.
∵OA=OB,OP=OP,
∴Rt△OAP≌ Rt△OBP,
∴PA=PB,∠APO=∠BPO.
1.PA、PB是☉O的两条切线,A、
B为切点,直线OP交☉O于点D、
E,交AB于C.
(1)写出图中所有的垂直关系;
OA⊥PA,OB ⊥PB,AB ⊥OP.
(3)写出图中所有的全等三角形;
△AOP≌ △BOP, △AOC≌ △BOC, △ACP≌ △BCP.
(4)写出图中所有的等腰三角形.△ABP △AOB
(2)写出图中与∠OAC相等的角;
∠OAC=∠OBC=∠APC=∠BPC.
P
练一练
P
2.PA、PB是☉O的两条切线,A,B是切点,OA=3.
(1)若AP=4,则OP= ;
(2)若∠BPA=60 °,则OP= .
5
6
3.如图,PA、PB是☉O的两条切线,点A、B是切点,在弧AB
上任取一点C,过点C作☉O的切线,分别交PA、PB于点D、E.
已知PA=7,∠P=40°.则
⑵ ∠DOE= .
⑴ △PDE的周长是 ;14
O
P
A
B
C
E
D
70°
解析:连接OA、OB、OC、OD和OE.∵PA、PB是☉O的
两条切线,点A、B是切点,
∴PA=PB=7.∠PAO=∠PBO=90°. ∠AOB=360°-∠PAO-
∠PBO-∠P=140°.
又∵DC、DA是☉O的两条切线,点C、A是切点,∴DC=DA.同理可得
CE=CB.
S△PDE=PD+DE+PE=PD+DC+CE+PE=PA+PB=14.
O
P
A
B
C
E
D
1
2
1
2
1
2
∵OA=OC,OD=OD,∴△AOD≌△COD,
∴∠DOC=∠DOA= ∠AOC.
同理可得∠COE= ∠COB.
∠DOE=∠DOC+∠COE= (∠AOC+
∠COB)=70°.
切线长问题辅助线添加方法:
(1)分别连接圆心和切点;
(2)连接两切点;
(3)连接圆心和圆外一点.
方法归纳
20 ° 4
如图,PA、PB是☉O的两条切线,切点分别是A、B,如果
AP=4, ∠APB= 40 ° ,则∠APO= ,PB= .
P
【练习】
如图,PA、PB是☉O的两条切线,切点为A、B,∠P= 50 °,
点C是☉O上异于A、B的点,则∠ACB= . 65 °或115 °
P
【小结】
切线长
切 线 长
定 理
作 用
图形的轴对称性原 理
提供了证线段和
角相等的新方法
辅助线
① 分别连接圆心和切点;
② 连接两切点;
③ 连接圆心和圆外一点.
相关文档
- 二年级语文下册课文419熟悉的脚印2021-05-24 09:49:4114页
- 2020-2021学年高三上学期月考数学(2021-05-24 09:48:416页
- 六年级上册数学课件-第5单元 第4课2021-05-24 09:48:4117页
- 【课件PPT人教版部编版】七年级语2021-05-24 09:48:4053页
- 八年级数学上册第六章数据的分析6-2021-05-24 09:48:382页
- 2020秋八年级英语上册Module52021-05-24 09:48:3615页
- 3-2-8 《分数除法的应用3》课件2021-05-24 09:48:2518页
- 教科版三年级上册科学课件《 水到2021-05-24 09:48:2218页
- 小学六年级作文教学课件(1)请到我的2021-05-24 09:48:0726页
- 【数学】2020届一轮复习人教A版填2021-05-24 09:47:537页