华师版数学八年级上册课件-第13章-13 三角形全等的判定 18页

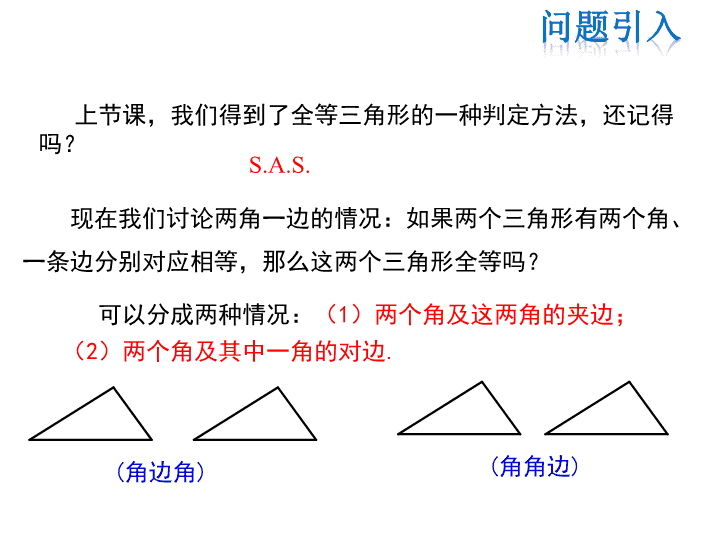
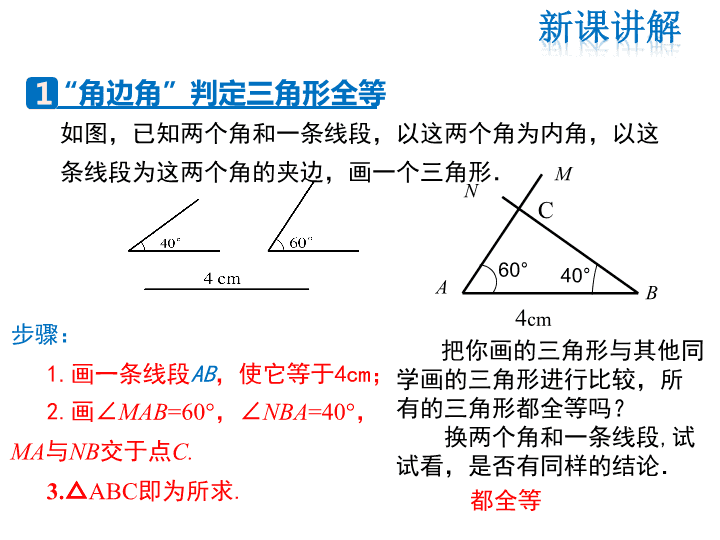
第13章 全等三角形 13.2 三角形全等的判定 3 边角边 上节课，我们得到了全等三角形的一种判定方法，还记得 吗？ S.A.S. 现在我们讨论两角一边的情况：如果两个三角形有两个角、 一条边分别对应相等，那么这两个三角形全等吗？ (角边角) (角角边) 可以分成两种情况：（1）两个角及这两角的夹边； （2）两个角及其中一角的对边. 如图，已知两个角和一条线段，以这两个角为内角，以这 条线段为这两个角的夹边，画一个三角形． 把你画的三角形与其他同 学画的三角形进行比较，所 有的三角形都全等吗？ 换两个角和一条线段,试 试看，是否有同样的结论． 都全等 60° 40° 4cm A B C 步骤： 1.画一条线段AB，使它等于4cm； 2.画∠MAB=60°，∠NBA=40°， MA与NB交于点C. 3.△ABC即为所求. M N “角边角”判定三角形全等1 下面用叠合的方法，看看你和你同伴所画的两个三 角形是否可以完全重合. Ａ Ｂ Ｃ Ｄ Ｅ Ｆ 全等 “角边角”判定方法 ▼文字语言：两角及其夹边分别相等的两个三角形全等(简写 成“角边角”或“A.S.A.”）. ▼几何语言： ∠A=∠A′ （已知）， AB=A′ B′ （已知）， ∠B=∠B′ （已知）， 在△ABC和△A′ B′ C′中， ∴ △ABC≌△ A′ B′ C′ （ASA）. A B C A ′ B ′ C ′ 【例1】 已知：∠ABC＝∠DCB，∠ACB＝ ∠DBC， 求证：△ABC≌△DCB,AB=DC． ∵∠ABC＝∠DCB(已知）， BC＝CB（公共边）， ∠ACB＝∠DBC（已知）， 证明：在△ABC和△DCB中， ∴△ABC≌△DCB（A.S.A. ）. ∴AB=DC(全等三角形的对应边相等) B C A D (角角边) 如图，如果两个三角形有两个角分别对应相等，且其中一 组相等的角的对边相等，那么这两个三角形是否一定全等？ 【思考】 分析：因为三角形的内角和等于180°，因此有两个角 对应相等，那么第三个角必定对应相等，于是有“角 边角”，可证得这两个三角形全等. “角角边”判定三角形全等2 已知：如图，∠A＝∠A′,∠B＝∠B′,AC＝A′C′. 求证：　△ABC≌△A′B′C′. 证明：∵∠A＝∠A′，∠B＝∠B′， ∠A＋∠B＋∠C＝180°， ∠A′＋∠B′＋∠C′＝180°(三角形内角和等于 180°)， ∴∠C＝∠C′（等量代换）． 在△ABC和△A′B′C′中， ∵∠A＝∠A′， AC＝A′C′， ∠C＝∠C′， ∴△ABC≌△A′B′C′（A.S.A.） “角角边”判定方法 ▼文字语言：有两角分别相等且其中一组等角的对边相等的 两个三角形全等(简写成“角角边”或“A.A.S.”）. ▼几何语言： ∠A=∠A′ （已知）， ∠B=∠B′ （已知）， AC=A′ C′ （已知）， 在△ABC和△A′ B′ C′中， ∴ △ABC≌△ A′ B′ C′ （A.A.S.）. A B C A ′ B ′ C ′ 【例2】 如图，点D在AB上，点E在AC上，AD=AE, ∠B=∠C, 求证：AB=AC. A B C D E 分析：证明△ACD≌△ABE,就可以得出AB=AC. 证明：在△ACD和△ABE中， ∠A=∠A（公共角 ）， ∠C=∠B （已知 ）， AD=AE（已知）， ∴ △ACD≌△ABE（A.A.S.）， ∴AB=AC. 已知：如图，△ABC ≌△A′B′C′ ，AD、A′ D′ 分别是△ABC 和 △A′B′C′的高.求证：AD＝ A′D′ . A B CD A ′ B ′ C ′D ′ 【例3】 求证：全等三角形对应边的高相等. 分析：从图中看出，AD、A′ D′ 分别属于△ABD 和△A′B′D′， 要证AD＝ A′D′，只需证明这两个三角形全等即可. 证明：∵△ABC ≌△A′B′C′ (已知)， ∴AB=A'B'（全等三角形的对应边相等）， ∠B=∠B'（全等三角形的对应角相等）. ∵AD⊥BC，A'D'⊥B'C'， ∴∠ADB=∠A'D'B'=90°（已知）. 在△ABD和△A'B'D'中， ∠ADB=∠A'D'B'=90°（已知）， ∠B=∠B'（已证）， AB=A'B'（已证）， ∴△ABD≌△A'B'D'.∴AD=A'D'. 归纳：全等三角形对 应边上的高也相等. 思考：全等三角形对应边上的中线、对应角的平分线又有什 么关系呢？你能说明其中的道理吗？ A B CD A ′ B ′ C ′D ′ 1. 如图，已知∠ACB=∠DBC，∠ABC=∠CDB，判别 下面的两个三角形是否全等，并说明理由. 解：不全等，因为BC虽然是 公共边，但不是对应边. A B C D 2.如图所示，OD=OB，AD∥BC，则全等三角形有( ) (A)2对 (B)3对 (C)4对 (D)5对 解析：根据题意得∠ADO=∠CBO，∠DOA=∠BOC，又 OD=OB，所以△DOA≌△BOC.同理可证△DOC≌△BOA， △DAB≌△BCD，△ACD≌△CAB，所以有4对. C 3.如图，某同学将一块三角形玻璃打碎成了三块，现要到玻 璃店去配一块完全一样的玻璃，那么最省事的办法是( ) (A)带(1)去 (B)带(2)去 (C)带(3)去 (D)带(1)(2)去 解析：题干中图(3)包含原三角形的两角一边，根据“A.S.A.” 可配一块与原三角形玻璃完全一样的玻璃. C A B C D E F 4.如图，∠ACB=∠DFE，BC=EF，那么应补充一个条 件 ，才能使△ABC≌△DEF （写出一个即可）. ∠B=∠E 或∠A=∠D 或 AC=DF （A.S.A.） （A.A.S.） （S.A.S.） AB=DE可以吗？ × AB∥DE 5.已知：如图， AB⊥BC，AD⊥DC，∠1=∠2, 求证：AB=AD. A C DB 1 2 证明： ∵ AB⊥BC，AD⊥DC， ∴ ∠ B=∠D=90 °. 在△ABC和△ADC中， ∠1=∠2 （已知）， ∠ B=∠D（已证）， AC=AC （公共边）， ∴ △ABC≌△ADC（A.A.S.). ∴AB=AD. 角 边 角 内 容 两角及其夹边分别相等的两个三 角形全等（简写成 “A.S.A.”) 应 用 为证明线段和角相等提供了新的证法 注 意 注意“角角边” “角边角” 中两角与边的区别