数学冀教版八年级上册课件13-3 全等三角形的判定 第4课时 17页

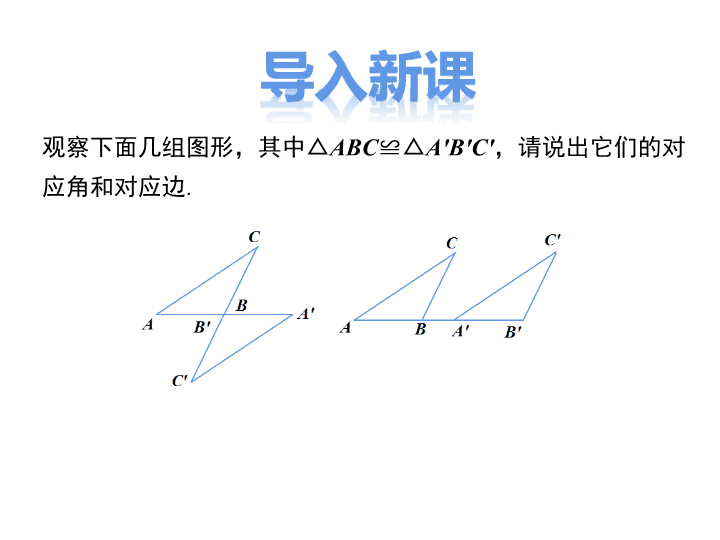
13.3 全等三角形的判定 导入新课 讲授新课 当堂练习 课堂小结 第4课时 具有特殊位置关系的三角形的全等 1.复习并回顾全等三角形的判定方法.（重点） 2.根据平移或旋转证明两个三角形全等并掌握其规律.（难 点） 观察下面几组图形，其中△ABC≌△A'B'C'，请说出它们的对 应角和对应边. 具有特殊位置关系的三角形的全等 如图，每组图形中的两个三角形都是全等三角形. 问题1 观察每组中的两个三角形，请你说出一个三角形经过怎样 的变换（平移或旋转）后，能够与另一个三角形的重合. 图① 图② 平移 平移 图④ 图⑤ 旋转 旋转 图③ 图⑥ 先旋转 后平移 先旋转 后平移 观察与思考 实际上，在我们遇到的两个全等三角形中，有些图 形具有特殊的位置关系，即其中一个三角形是由另一个 三角形经过平移或旋转（有时是两种变换）得到的.发 现两个三角形间的这种特殊关系，能够帮助我们找到命 题证明的途径，较快解决问题. 例1 已知：如图，在△ABC中，D是BC的中点，DE∥AB， 交AC于点E，DF∥AC，交AB于点F. 求证：△BDF≌△DCE. 证明：∵D是BC的中点（已知）， ∴BD=DC（线段中点定义）. ∵DE∥AB，DF∥AC（已知）， ∴∠B=∠EDC，∠BDF=∠C（两直 线平行，同位角相等）， 在△BDF和△DCE中， ∠B=∠EDC， BD=DC， ∠BDF=∠C. ∴△BDF≌△DCE（ASA）. 例2 已知：如图，在△ABC中，D，E分别是AB，AC的 中点，CF∥AB，交DE的延长线于点F. 求证：DE=FE. 证明：∵CF∥AB（已知）， ∴∠A=∠ECF（两直线平行，内错角相等）. 在△EAD和△ECF中， ∠A=∠ECF， AE=CE， ∠AED=∠CEF（对顶角相等）， ∴△EAD≌△ECF（ASA）. ∴DE=FE（全等三角形的对应边相等）. 1.已知，如图，AB∥CD，BF∥DE且AE=2，AC=10，则 EF=_______.6 2.已知：如图，BE=CF，AB∥ED，AC∥DF. 求证：△ABC≌△DEF. 证明：∵AB∥ED，AC∥DF（已知）， ∴∠B=∠DEF，∠F=∠ACB（两直线 平行，同位角相等）. ∵BE=CF，∴BE+EC=CF+EC（等式的 性质），即BC=EF. 在△ABC和△DEF中， ∠B=∠DEF（已推出）， BC=EF（已推出） ∠F=∠ACB（已推出）， ∴△ABC≌△DEF（ASA）. A B C D E F 3.已知：如图， AB⊥BC，AD⊥DC，∠1=∠2, 求证：AB=AD. A C DB 1 2 证明： ∵ AB⊥BC，AD⊥DC， ∴ ∠ B=∠D=90 °. 在△ABC和△ADC中， ∠1=∠2 （已知）， ∠ B=∠D（已证）， AC=AC （公共边）， ∴ △ABC≌△ADC（AAS)， ∴AB=AD. u平移全等形 u旋转全等形 u翻折全等形