- 63.82 KB
- 2021-04-16 发布
1.4 《平行线的性质》
学习本节之前同学们已经在教材及课本中认识了平行线及“三线八角”,本节主要从三个角
度教授同学们平行线的三个性质即可。
【知识与能力目标】
掌握平行线的三个特征,体会平行线特征与平行线识别的区别,能运用平行线的识别与特征
解决问题。
【过程与方法目标】
经历观察、操作、推理、交流等活动,一步发展空间观念,加强推理能力和有条理的表达能
力,经历探索平行线的特征的过程,掌握平行线的特征并解决一些问题。
【情感态度价值观目标】
通过操作、观察、合作、交流,进一步感受学习数学的意义,培养学生主动探索、合作以及
解决问题的能力。
【教学重点】
平行线的特征。
【教学难点】
平行线的特征与识别法的综合运用。
多媒体、投影仪等。
(一)创设情境,激趣引入
1.复习和巩固平行线的判定方法,并引导学生总结平行线的判定是由角的数量关系得出线的
位置的结论
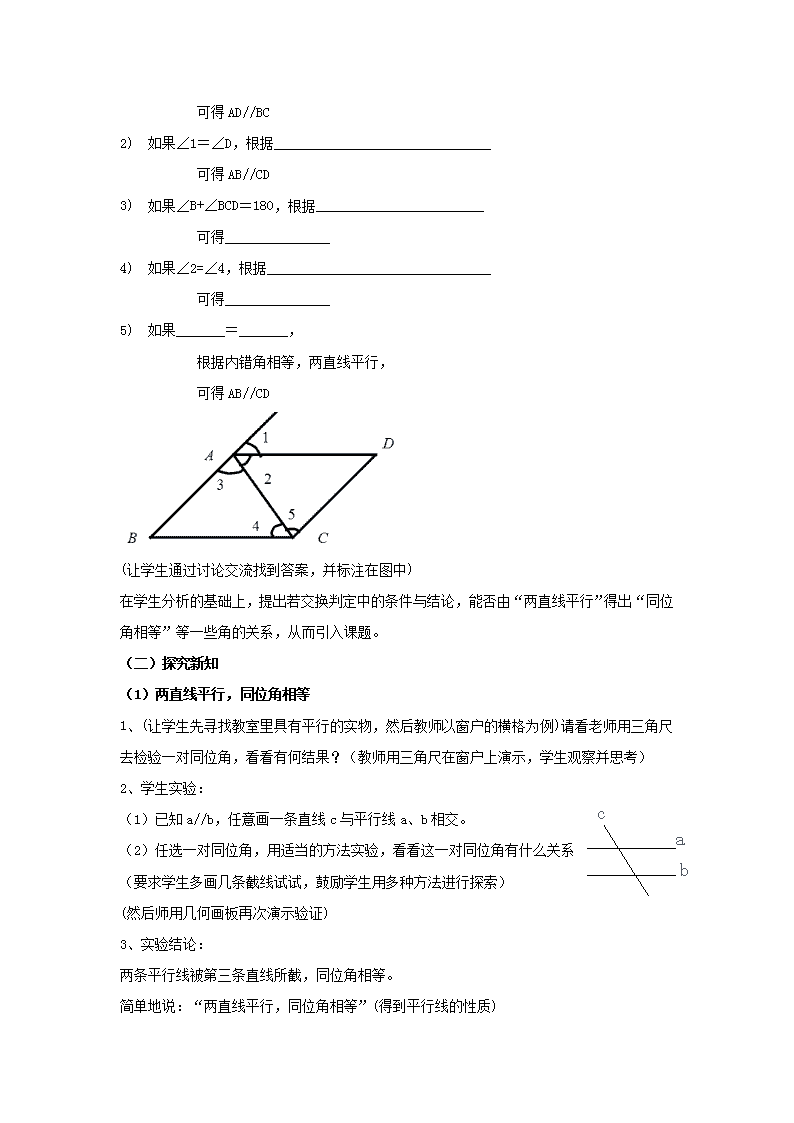
2.试一试: 1) 如果∠B=∠1,根据_______________________________
◆ 教材分析
◆ 教学目标
◆ 教学重难点
◆
◆ 课前准备
◆
◆ 教学过程
可得 AD//BC
2) 如果∠1=∠D,根据_______________________________
可得 AB//CD
3) 如果∠B+∠BCD=180,根据________________________
可得_______________
4) 如果∠2=∠4,根据________________________________
可得_______________
5) 如果_______=_______,
根据内错角相等,两直线平行,
可得 AB//CD
(让学生通过讨论交流找到答案,并标注在图中)
在学生分析的基础上,提出若交换判定中的条件与结论,能否由“两直线平行”得出“同位
角相等”等一些角的关系,从而引入课题。
(二)探究新知
(1)两直线平行,同位角相等
1、(让学生先寻找教室里具有平行的实物,然后教师以窗户的横格为例)请看老师用三角尺
去检验一对同位角,看看有何结果?(教师用三角尺在窗户上演示,学生观察并思考)
2、学生实验:
(1)已知 a//b,任意画一条直线 c 与平行线 a、b 相交。
(2)任选一对同位角,用适当的方法实验,看看这一对同位角有什么关系
(要求学生多画几条截线试试,鼓励学生用多种方法进行探索)
(然后师用几何画板再次演示验证)
3、实验结论:
两条平行线被第三条直线所截,同位角相等。
简单地说:“两直线平行,同位角相等”(得到平行线的性质)
c
a
b
指出:1)同位角相等是平行线特有的性质(以消除”凡是同位角都相等”;”两直线被第三
条直线所截,同位角相等”的错误判断)
2)它与前面学过的“同位角相等,两直线平行”之间的区别(通过形象板书示范予以直观说
明)。
3)数学表达式:
∵ a//b (已知)
∴ ∠1=∠2 (两直线平行,同位角相等)
(2)两直线平行,内错角相等
在教师提出问题的条件下,学生自己动手,实际操作,进行度量,在有了大量感性认识的基
础上,动脑分析总结出结论,不仅充分发挥学生主体作用,而且培养了学生分析问题的能力。
提出问题:请同学们观察图 2-62 的图形,两条平行线被第三条直线所截,同位角是相等的,
那么内错角、同旁内角有什么关系呢?
学生活动:学生观察分析思考,会很容易地答出内错角相等,同旁内角互补。
师:教师继续提问,你能论述为什么内错角相等,同旁内角互补吗?同学们可以讨论一下。
学生活动:学生们思考,并相互讨论后,有的同学举手回答。
在前面复习引入的第 2 题的基础上,通过学生的观察、分析、讨论,此时学生已能够进行推
理,在这里教师不必包办代替,充分调动学生的主动性和积极性,进而培养学生分析问题的
能力,在学生有成就感的同时也激励了学生的学习兴趣。
教师根据学生回答,给予肯定或指正的同时板书。
[板书]∵a∥b(已知),
∴∠1=∠2(两条直线平行,同位角相等)
∵∠1=∠3(对顶角相等),
∴∠2=∠3(等量代换)。
师:由此我们又得到了平行线有怎样的性质呢?
学生活动:同学们积极举手回答问题。
教师根据学生叙述,给出板书:
[板书]两条平行线被第三条直线所截,内错角相等。
简单说成:两直线平行,内错角相等。
(3)两直线平行,同房内角互补
师:下面请同学们自己推导同旁内角是互补的.并归纳总结出平行线的第三条性质。
请一名同学到黑板上板演,其他同学在练习本上完成。
师生共同订正推导过程和第三条性质,形成正确板书。
[板书]∵a∥b(已知)
∴∠1=∠2(两直线平行,同位角相等)
∵∠1+∠4=180°(邻补角定义)
∴∠2+∠4=180°(等量代换)
即:两条平行线被第三条直线所截,同旁内角互补,简单说成,两直线平行,同旁内角互补
师:我们知道了平行线的性质,在今后我们经常要用到它们去解决、论述一些问题,所需要
知道的条件是两条直线平行,才有同位角相等,内错角相等,同旁内角互补,即它们的符号
语言分别为:
∵a∥b(已知见图 2-63),
∴∠1=∠2(两直线平行,同位角相等)
∵a∥b(已知),
∴∠2=∠3(两直线平行,内错角相等)
∵a∥b(已知),
∴∠2+∠4=180°。
(两直线平行,同旁内角互补)(板书在三条性质对应位置上)。
(三)应用反馈,巩固新知
略。
◆ 教学反思
您可能关注的文档
相关文档
- 2018-2019学年贵州省安顺市平坝第2021-04-16 10:01:2518页
- 2020高中数学 课时分层作业17 不等2021-04-16 10:01:125页
- 2020七年级数学上册 第1章 有理数 2021-04-16 10:00:586页
- 陕西省渭南市临渭区尚德中学2019-22021-04-16 10:00:5214页
- 【生物】2018届一轮复习人体生命活2021-04-16 10:00:409页
- 2017届高考文科数学(全国通用)二轮适2021-04-16 10:00:168页
- 高中数学人教a版必修五章末综合测2021-04-16 10:00:119页
- 2019年高考数学复习大二轮精准提分2021-04-16 10:00:0262页
- 六年级上册数学课件-4 比的意义 ︳人2021-04-16 09:59:5421页
- 2019高三数学文北师大版一轮重点强2021-04-16 09:59:537页