- 2.76 MB
- 2024-06-04 发布
滚动小专题(七)与三角形有关的计算与证明(解答题)
类型1 全等三角形性质与判定的综合运用
类型2 相似三角形性质与判定的综合运用
类型3 全等三角形、相似三角形的综合运用
类型1 全等三角形性质与判定的综合运用
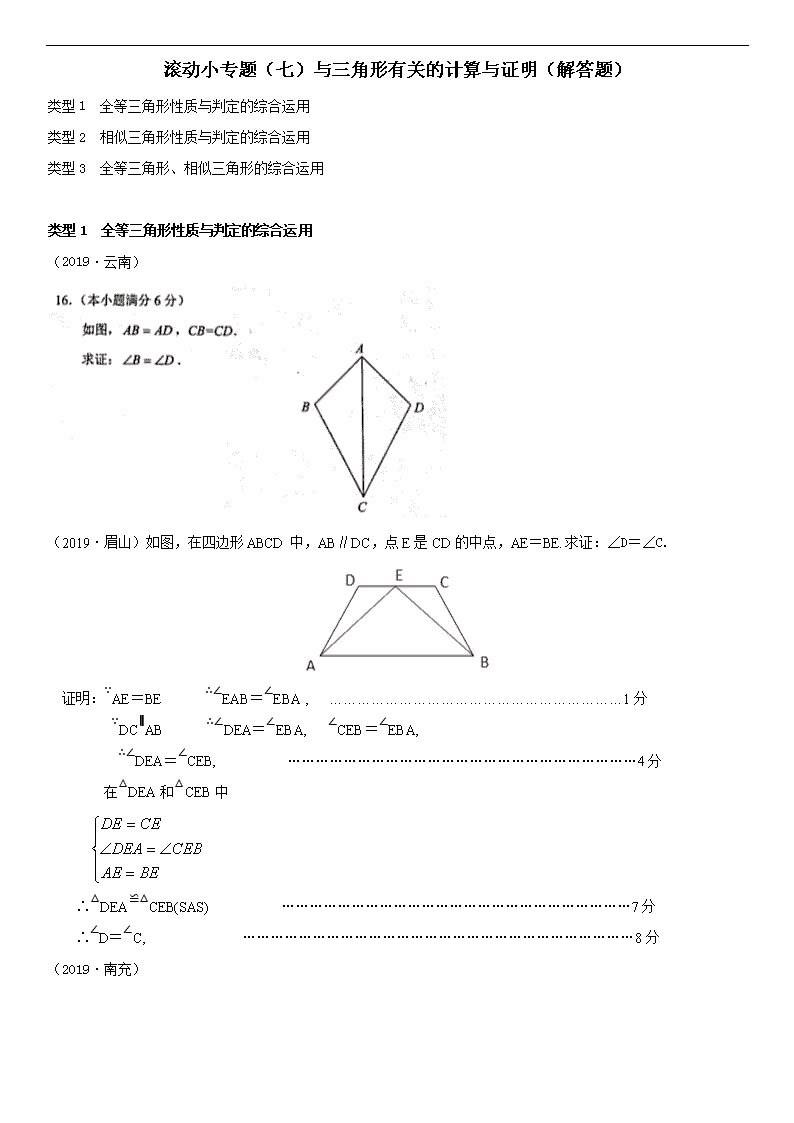
(2019·云南)
(2019·眉山)如图,在四边形ABCD中,AB∥DC,点E是CD的中点,AE=BE.求证:∠D=∠C.
证明:∵AE=BE ∴∠EAB=∠EBA , ………………………………………………………1分
∵DC∥AB ∴∠DEA=∠EBA, ∠CEB=∠EBA,
∴∠DEA=∠CEB, …………………………………………………………………4分
在△DEA和△CEB中
∴△DEA≌△CEB(SAS) …………………………………………………………………7分
∴∠D=∠C, …………………………………………………………………………8分
(2019·南充)
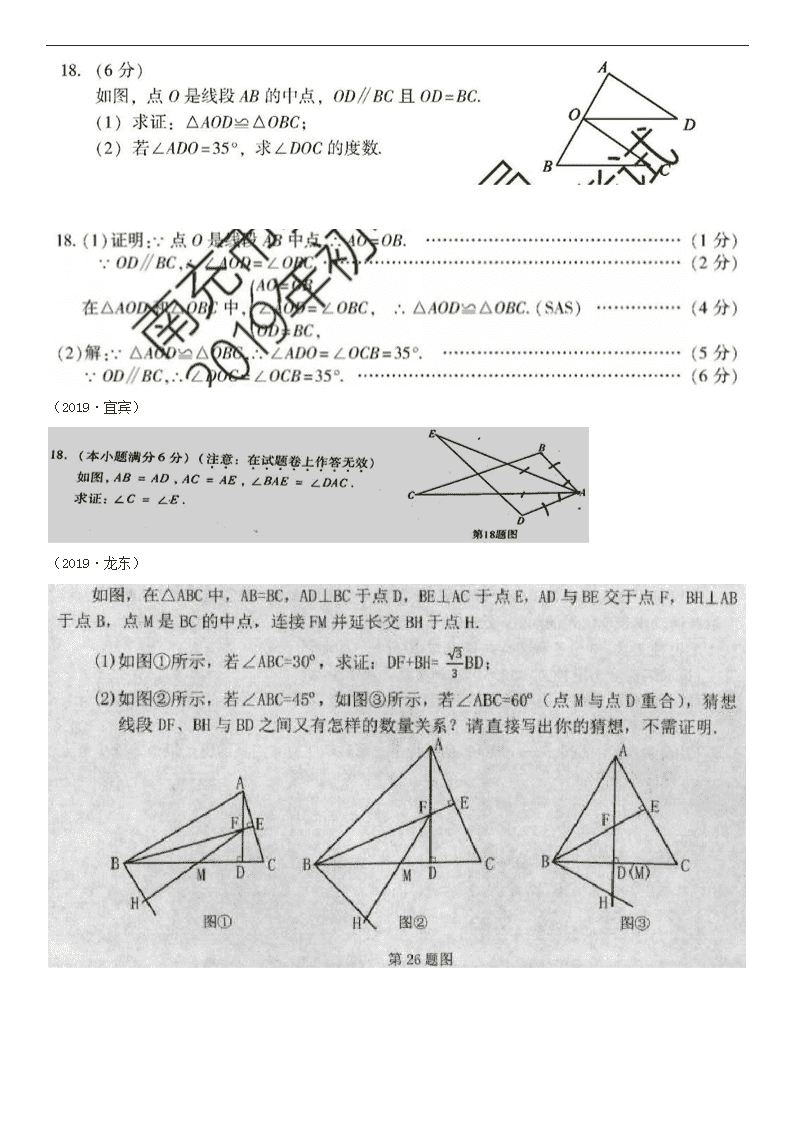
(2019·宜宾)
(2019·龙东)
(2019·桂林)
(2019·巴中)
(2019·兰州)
(2019·武汉)如图,点A、B、C、D在一条直线上,CE与BF交于点G,∠A=∠1,CE∥DF,求证:∠E=∠F.
(2019·温州)
(2019·淄博)
(2019·无锡)如图,在△ABC中,AB=AC,点D、E分别在AB、AC上,BD=CE,BE、CD相交于点O.
(1)求证:△DBC≌△ECB;
(2)求证:OB=OC.
证明:(1)∵AB=AC,∴∠ECB=∠DBC.
在
∴ .
(2)由(1)知,,∴∠DCB=∠EBC.
∴OB=OC.
(2019· 乐山)如图,线段、相交于点, ,.求证:.
证明:在和中,
,,,
≌.
故.
(2019·广州)如图8,D是AB上一点,DF交AC于点E,DE=FE,FC∥AB,求证:.
证明:∵FC∥AB
∴∠A=∠FCE,∠ADE=∠F
所以在△ADE与△CFE中:
∴△ADE≌△CFE
(2019·黄石)
(2019·孝感)如图,已知∠C=∠D=90°,BC与AD交于点E,AC=BD,求证:AE=BE.
(2019·宜昌)
(2019·山西)
(2019·泸州)如图,AB∥CD,AD和BC相交于点O,OA=OD.求证:OB=OC.
(2019·苏州)
(2019·安顺)
类型2 相似三角形性质与判定的综合运用
(2019·凉山州)
类型3 全等三角形、相似三角形的综合运用