2015年高考真题——理科数学（四川卷）原卷版 4页

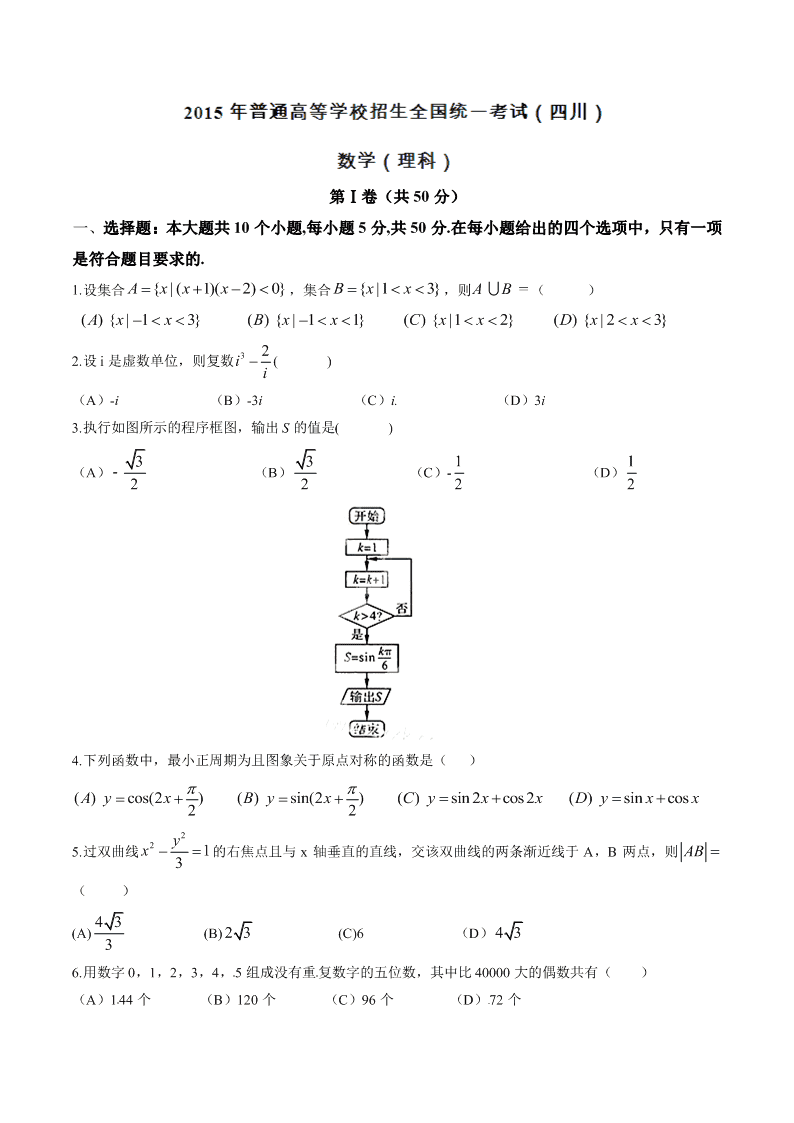
第Ⅰ卷（共 50 分） 一、选择题：本大题共 10 个小题,每小题 5 分,共 50 分.在每小题给出的四个选项中，只有一项 是符合题目要求的. 1.设集合 { | ( 1)( 2) 0}A x x x    ，集合 { |1 3}B x x   ，则AB= （ ） ( ) { | 1 3}A x x   ( ) { | 1 1}B x x   ( ) { |1 2}C x x ( ) { | 2 3}D x x 2.设 i 是虚数单位，则复数 3 2i i ( ) （A）-i （B）-3i （C）i. （D）3i 3.执行如图所示的程序框图，输出 S 的值是( ) （A） 3 2- （B） 3 2 （C）- 1 2 （D） [来源:学,科,网 Z,X,X,K] 4.下列函数中，最小正周期为且图象关于原点对称的函数是（ ） ( ) cos(2 )2A y x  ( ) sin(2 )2B y x  ( ) sin 2 cos2C y x x ( ) sin cosD y x x 5.过双曲线 2 2 13 yx 的右焦点且与 x 轴垂直的直线，交该双曲线的两条渐近线于 A，B 两点，则 AB  （ ）[来源:学&科&网] (A) 43 3 (B) 23 (C)6 （D） 43 6.用数字 0，1，2，3，4，5 组成没有重复数字的五位数，其中比 40000 大的偶数共有（ ） （A）144 个 （B）120 个 （C）96 个 （D）72 个 7.设四边形 ABCD 为平行四边形， 6AB  ， 4AD  .若点 M，N 满足 3BM MC ， 2DN NC ，则 AM NM（ ） （A）20 （B）15 （C）9 （D）6 8.设 a，b 都是不等于 1 的正数，则“3 3 3ab”是“log 3 log 3ab ”的 （ ） （A）充要条件 （B）充分不必要条件 （C）必要不充分条件 （D）既不充分也不必要条件[来源:学#科#网 Z#X#X#K] 9.如果函数        21 2 8 1 0 02f x m x n x m n      ， 在区间 1 22   ， 上单调递减，则 mn 的最大值 为（ ） （A）16 （B）18 （C）25 （D） 81 2 10.设直线 l 与抛物线 2 4yx 相交于 A，B 两点，与圆   2 2250x y r r    相切于点 M，且 M 为线段 AB 的中点.若这样的直线 l 恰有 4 条，则 r 的取值范围是（ ） （A） 13， （B） 14， （C） 23， （D） 24， 第Ⅱ卷（共 100 分） 二、填空题（每题 5 分，满分 25 分，将答案填在答题纸上） 11.在 5(2 1)x  的展开式中，含 2x 的项的系数是 （用数字作答）. 12.   75sin15sin . 13.某食品的保鲜时间 y（单位：小时）与储存温度 x（单位： C ）满足函数关系 bkxey  （ 718.2e 为 自然对数的底数，k、b 为常数）。若该食品在 0 的保鲜时间设计 192 小时，在 22 的保鲜时间是 48 小 时，则该食品在 33 的保鲜时间是 小时.[来源:学#科#网] 14.如图，四边形 ABCD 和 ADPQ 均为正方形，它们所在的平面互相垂直，动点 M 在线段 PQ 上，E、F 分 别为 AB、BC 的中点。设异面直线 EM 与 AF 所成的角为 ，则 cos 的最大值为 . 15.已知函数 xxf 2)(  ， axxxg  2)( （其中 Ra ）.对于不相等的实数 21, xx ，设 21 21 )()( xx xfxfm   ， 21 21 )()( xx xgxgn   . 现有如下命题：[来源:学&科&网] （1）对于任意不相等的实数 ，都有 0m ； （2）对于任意的 a 及任意不相等的实数 ，都有 0n ； （3）对于任意的 a，存在不相等的实数 ，使得 nm  ； （4）对于任意的 a，存在不相等的实数 ，使得 nm  . 其中的真命题有 （写出所有真命题的序号）. 三、解答题 （本大题共 6 小题，共 75 分.解答应写出文字说明、证明过程或演算步骤.） 16.设数列{}na 的前 n 项和 12nnS a a，且 1 2 3, 1,a a a 成等差数列. （1）求数列 的通项公式； （2）记数列 1{} na 的前 n 项和 nT ，求得 1| 1| 1000nT  成立的 n 的最小值. 17.某市 A,B 两所中学的学生组队参加辩论赛，A 中学推荐 3 名男生，2 名女生，B 中学推荐了 3 名男生，4 名女生，两校推荐的学生一起参加集训，由于集训后队员的水平相当，从参加集训的男生中随机抽取 3 人， 女生中随机抽取 3 人组成代表队 （1）求 A 中学至少有 1 名学生入选代表队的概率. （2）某场比赛前，从代表队的 6名队员中随机抽取 4 人参赛，设 X 表示参赛的男生人数，求 X 得分布列和 数学期望. 18.一个正方体的平面展开图及该正方体的直观图的示意图如图所示，在正方体中，设 BC 的中点为 M ，GH 的中点为 N （1）请将字母 ,,F G H 标记在正方体相应的顶点处（不需说明理由） （2）证明：直线 //MN 平面 BDH （3）求二面角 A EG M的余弦值. 19.如图，A，B，C，D 为平面四边形 ABCD 的四个内角. （1）证明： 1 costan ;2 sin AA A  （2）若 180 , 6, 3, 4, 5,A C AB BC CD AD     o 求 tan tan tan tan2 2 2 2 A B C D   的值. 20.如图，椭圆 E： 22 22+ 1( 0)xy abab   的离心率是 2 2 ，过点 P（0,1）的动直线l 与椭圆相交于 A，B 两点，当直线 平行与 x 轴时，直线 被椭圆 E 截得的线段长为 22. (1)求椭圆 E 的方程； (2)在平面直角坐标系 xOy 中，是否存在与点 P 不同的定点 Q，使得 QA PA QB PB 恒成立？若存在，求出 点 Q 的坐标；若不存在，请说明理由. 21.已知函数 22( ) 2( )ln 2 2f x x a x x ax a a       ，其中 0a  . （1）设 ()gx是 ()fx的导函数，评论 的单调性； （2）证明：存在 (0,1)a ，使得 ( ) 0fx 在区间 (1,+ )内恒成立，且 ( ) 0fx 在 (1,+ )内有唯一解.