- 599.50 KB
- 2021-06-19 发布
2012江苏高考数学试卷
参考公式:
(1) 样本数据x1 ,x2 ,…,xn的方差s2=(xi -)2,其中.
(2) (2)直棱柱的侧面积S=ch ,其中c为底面积,h 为高.
(3)棱柱的体积V= Sh ,其中S为底面积,h 为高.
一.填空题:本大题共14小题,每小题5分,共计70分,请把答案填写在答题卡的相应位置上。
1、已知集合 则
2、函数的单调增区间是__________
3、设复数i满足(i是虚数单位),则的实部是_________
4、根据如图所示的伪代码,当输入分别为2,3时,最后输出的m的值是________
Read a,b
If a>b Then
ma
Else
mb
End If
Print m
5、从1,2,3,4这四个数中一次随机取两个数,则其中一个数是另一个的两倍的概率是______
6、某老师从星期一到星期五收到信件数分别是10,6,8,5,6,则该组数据的方差
7、已知 则的值为__________
8、在平面直角坐标系中,过坐标原点的一条直线与函数的图象交于P、Q两点,则线段PQ长的最小值是________
9、函数是常数,的部分图象如图所示,则
10、已知是夹角为的两个单位向量, 若,则k的值为
11、已知实数,函数,若,则a的值为________
12、在平面直角坐标系中,已知点P是函数的图象上的动点,该图象在P处的切线交y轴于点M,过点P作的垂线交y轴于点N,设线段MN的中点的纵坐标为t,则t的最大值是_____________
13、设,其中成公比为q的等比数列,成公差为1的等差数列,则q的最小值是________
14、设集合,
, 若 则实数m的取值范围是______________
二、解答题:本大题共6小题,共计90分,请在答题卡指定区域内作答,解答时应写出文字说明、证明过程活盐酸步骤。
15、在△ABC中,角A、B、C所对应的边为
(1)若 求A的值;(2)若,求的值.
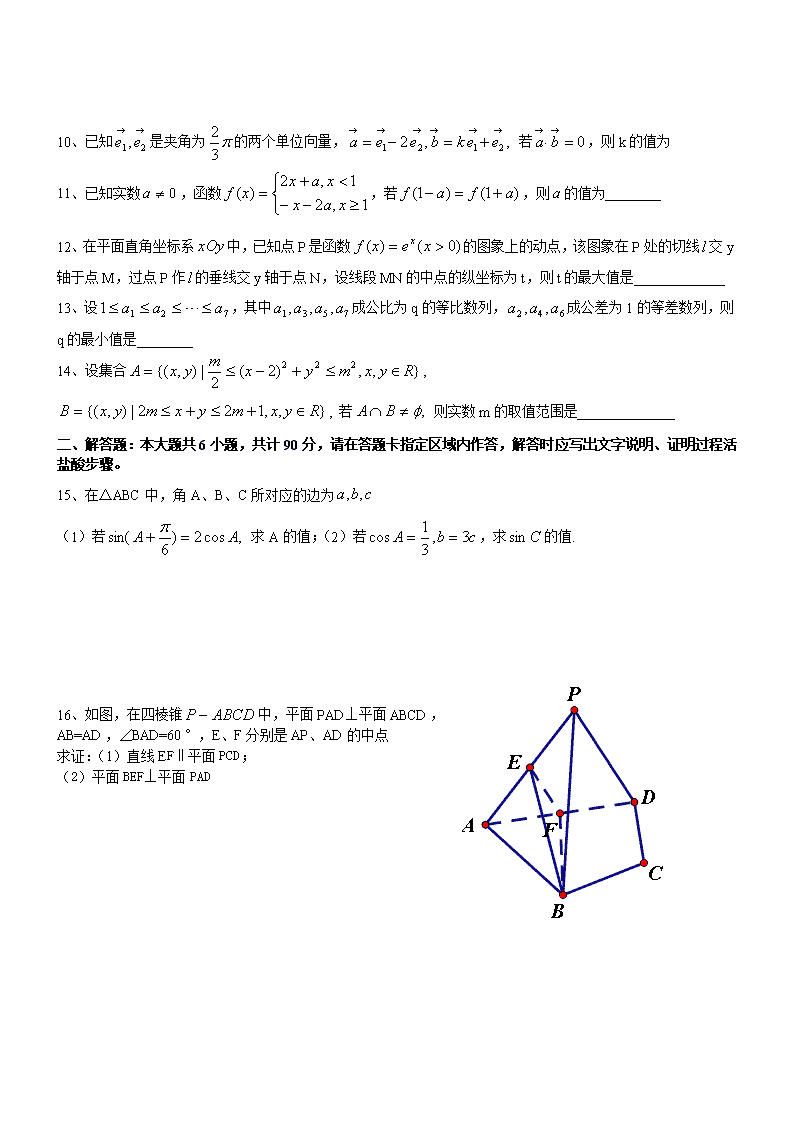
16、如图,在四棱锥中,平面PAD⊥平面ABCD,
AB=AD,∠BAD=60°,E、F分别是AP、AD的中点
求证:(1)直线EF‖平面PCD;
(2) 平面BEF⊥平面PAD
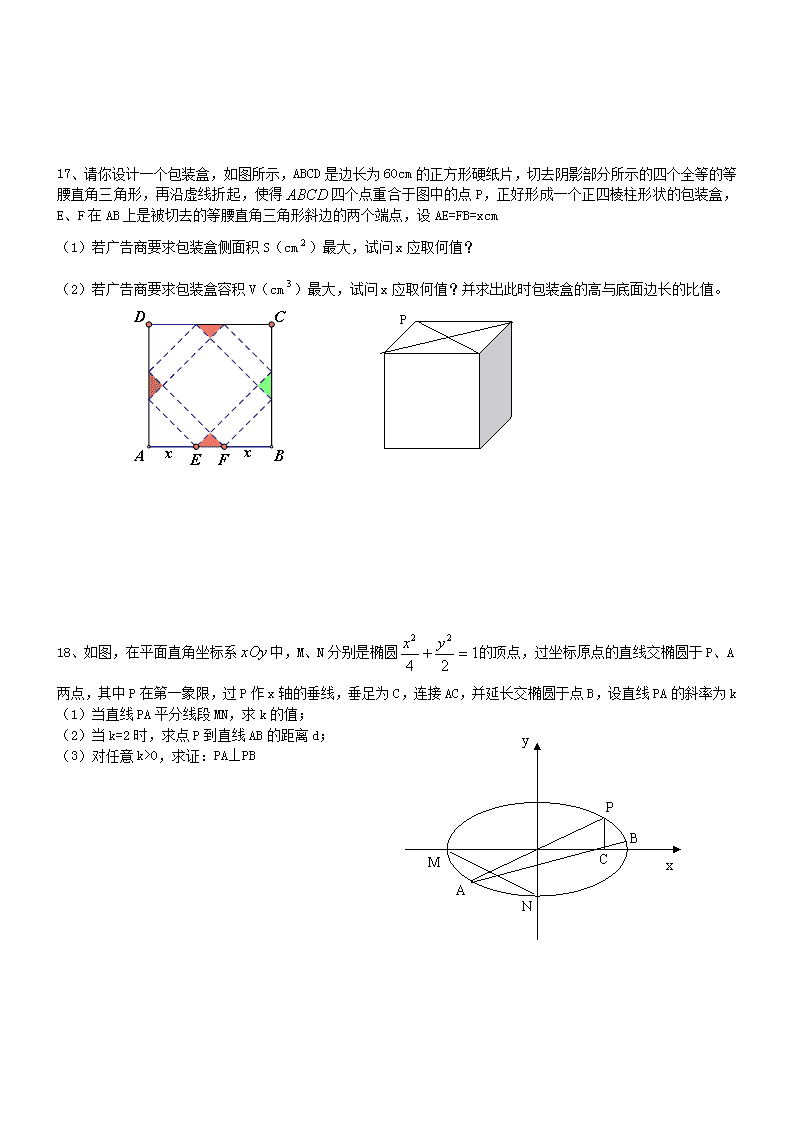
17、请你设计一个包装盒,如图所示,ABCD是边长为60cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,E、F在AB上是被切去的等腰直角三角形斜边的两个端点,设AE=FB=xcm
(1)若广告商要求包装盒侧面积S(cm)最大,试问x应取何值?
(2)若广告商要求包装盒容积V(cm)最大,试问x应取何值?并求出此时包装盒的高与底面边长的比值。
P
18、如图,在平面直角坐标系中,M、N分别是椭圆的顶点,过坐标原点的直线交椭圆于P、A两点,其中P在第一象限,过P作x轴的垂线,垂足为C,连接AC,并延长交椭圆于点B,设直线PA的斜率为k
(1)当直线PA平分线段MN,求k的值;
N
M
P
A
x
y
B
C
(2)当k=2时,求点P到直线AB的距离d;
(3)对任意k>0,求证:PA⊥PB
19、已知a,b是实数,函数 和是的导函数,若在区间I上恒成立,则称和在区间I上单调性一致
(1)设,若函数和在区间上单调性一致,求实数b的取值范围;
(2)设且,若函数和在以a,b为端点的开区间上单调性一致,求|a-b|的最大值
20、设M为部分正整数组成的集合,数列的首项,前n项和为,已知对任意整数k属于M,当n>k时,都成立
(1)设M={1},,求的值;(2)设M={3,4},求数列的通项公式
(2)设M={3,4},求数列的通项公式
相关文档
- 2020高考化学二轮复习课时作业7电2021-06-19 20:58:1311页
- 2020版高考物理一轮复习第二章 微2021-06-19 20:58:015页
- 2020届山东省枣庄市滕州一中高三上2021-06-19 20:57:4911页
- 《宪法小卫士》初中组答案汇总2021-06-19 20:56:3816页
- 语文卷·2019届江苏省扬州中学高二2021-06-19 20:56:267页
- 精选电大护理学基础期末考试【最新2021-06-19 20:55:398页
- 专题3-1+牛顿第一定律+牛顿第三定2021-06-19 20:55:275页
- 高考地理专题二十 世界地理2021-06-19 20:55:03125页
- PEP小学英语五年级上册测试题及答2021-06-19 20:54:395页
- 2020年高考真题——化学(天津卷) Wor2021-06-19 20:53:1310页