2014年高考真题——理科数学（福建卷） 原卷版 6页

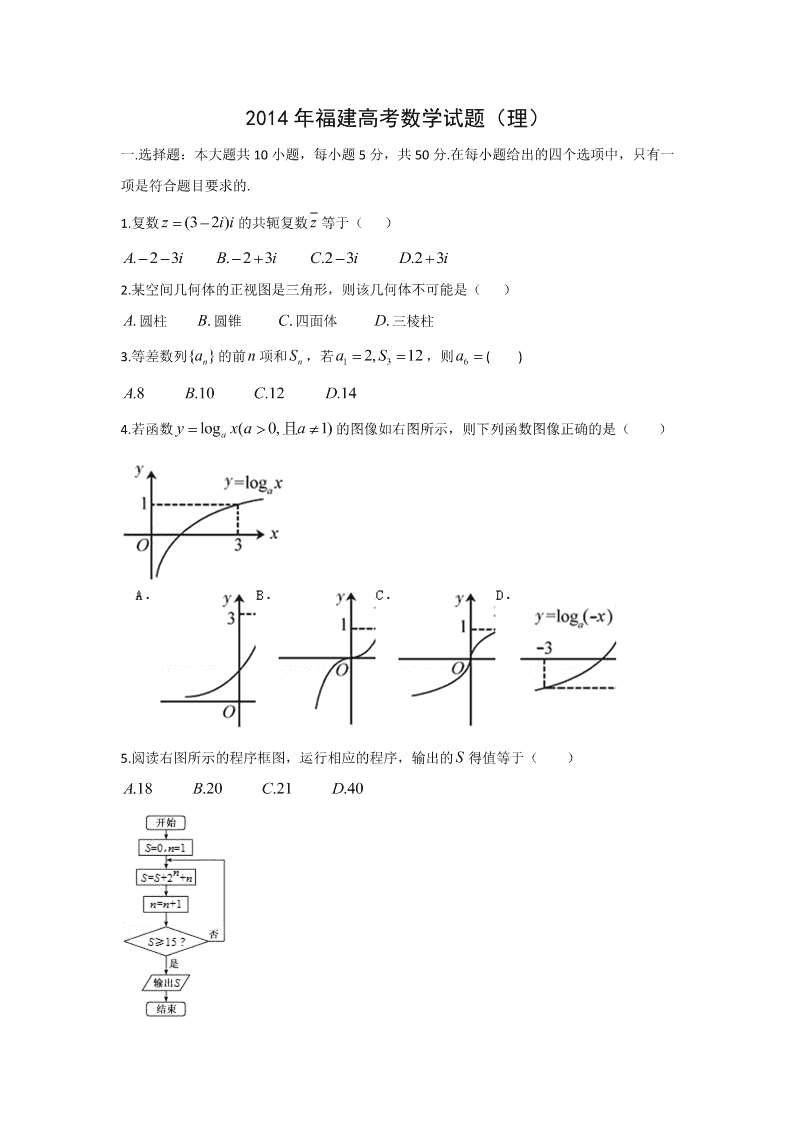
2014 年福建高考数学试题（理） 一.选择题：本大题共 10 小题，每小题 5 分，共 50 分.在每小题给出的四个选项中，只有一 项是符合题目要求的. 1.复数 (3 2 )z i i 的共轭复数 z 等于（ ） . 2 3Ai . 2 3Bi .2 3Ci .2 3Di 2.某空间几何体的正视图是三角形，则该几何体不可能是（ ） .A 圆柱 .B 圆锥 .C 四面体 .D三棱柱 3.等差数列{}na 的前 n 项和 nS ，若 132, 12aS，则 6a  ( ) .8A .10B .12C .14D 4.若函数 log ( 0, 1)ay x a a  且 的图像如右图所示，则下列函数图像正确的是（ ） 5.阅读右图所示的程序框图，运行相应的程序，输出的 S 得值等于（ ） .18A .20B .21C .40D 6.直线 :1l y kx与圆 22:1O x y相交于 ,AB两点，则" 1"k  是“ ABC 的面积为 1 2 ” 的（ ） .A 充分而不必要条件 .B 必要而不充分条件 .C 充分必要条件 .D 既不充分又不必要条件 7.已知函数        0,cos 0,12 xx xxxf 则下列结论正确的是（ ） A.  xf 是偶函数 B. 是增函数 C. 是周期函数 D. 的值域为  ,1 8.在下列向量组中，可以把向量  2,3a 表示出来的是（ ） A. )2,1(),0,0( 21  ee B . )2,5(),2,1( 21  ee C. )10,6(),5,3( 21  ee D. )3,2(),3,2( 21  ee 9.设 QP, 分别为   26 22  yx 和椭圆 110 2 2  yx 上的点，则 两点间的最大距离是 （ ） A. 25 B. 246  C. 27 D. 26 10.用 a 代表红球，b 代表蓝球，c 代表黑球，由加法原理及乘法原理，从 1 个红球和 1 个篮 球中取出若干个球的所有取法可由  ba  11 的展开式 abba 1 表示出来，如：“1” 表示一个球都不取、“ ”表示取出一个红球，面“ ab ”用表示把红球和篮球都取出来.以 此类推，下列各式中，其展开式可用来表示从 5 个无区别的红球、5 个有区别的黑球中取出 若干个球，且所有的篮球都取出或都不取出的所有取法的是 A.    555432 111 cbaaaaa  B.    554325 111 cbbbbba  C.     554325 111 cbbbbba  D.     543255 111 cccccba  二、填空题 11、若变量 yx, 满足约束条件       0 082 01 x yx yx 则 yxz  3 的最小值为________ 12、在 ABC 中， 3,2,60  BCACA ,则 ABC 等于_________ 13、要制作一个容器为 4 3m ，高为 m1 的无盖长方形容器，已知该容器的底面造价是每平方 米 20 元，侧面造价是每平方米 10 元，则该容器的最低总造价是_______（单位：元） 14.如图，在边长为e（ 为自然对数的底数）的正方形中随机撒一粒黄豆，则他落到阴影部 分的概率为______. 15.若集合 },4,3,2,1{},,,{ dcba 且下列四个关系： ① 1a ；② 1b ；③ 2c ；④ 4d 有且只有一个是正确的，则符合条件的有序数组 ),,,( dcba 的个数是_________. 三．解答题：本大题共 6 小题，共 80 分. 16.（本小题满分 13 分） 已知函数 1( ) cos (sin cos ) 2f x x x x   . （1）若 0 2 ，且 2sin 2  ，求 ()f  的值； （2）求函数 ()fx的最小正周期及单调递增区间. 17.（本小题满分 12 分） 在平行四边形 ABCD 中， 1AB BD CD   ， ,AB BCD CD BD.将 ABD 沿 BD 折起，使得平面 ABD  平面 BCD，如图. （1）求证：CD  CD ； （2）若 M 为 AD 中点，求直线 AD 与平面 MBC 所成角的正弦值. 18.（本小题满分 13 分） 为回馈顾客，某商场拟通过摸球兑奖的方式对 1000 位顾客进行奖励，规定：每位顾客从 一个装有 4 个标有面值的球的袋中一次性随机摸出 2 个球，球上所标的面值之和为该顾 客所获的奖励额. （1）若袋中所装的 4 个球中有 1 个所标的面值为 50 元，其余 3 个均为 10 元，求 ①顾客所获的奖励额为 60 元的概率 ②顾客所获的奖励额的分布列及数学期望; （2）商场对奖励总额的预算是 60000 元，并规定袋中的 4 个球只能由标有面值 10 元和 50 元的两种球组成，或标有面值 20 元和 40 元的两种球组成.为了使顾客得到的奖励 总额尽可能符合商场的预算且每位顾客所获的奖励额相对均衡，请对袋中的 4 个球 的面值给出一个合适的设计，并说明理由. 19.（本小题满分 13 分） 已知双曲线 )0,0(1: 2 2 2 2  bab y a xE 的两条渐近线分别为 xylxyl 2:,2: 21  . （1）求双曲线 E 的离心率； （2）如图，O 为坐标原点，动直线l 分别交直线 21,ll 于 BA, 两点（ BA, 分别在第一， 四象限），且 OAB 的面积恒为 8，试探究：是否存在总与直线l 有且只有一个公 共点的双曲线 E ？若存在，求出双曲线 E 的方程；若不存在，说明理由。 20. （本小题满分 14 分） 已知函数   axexf x  （ a 为常数）的图像与 y 轴交于点 A ，曲线  xfy  在点 处 的切线斜率为-1. （I）求 的值及函数  xf 的极值； （II）证明：当 0x 时， xex 2 ； （III）证明：对任意给定的正数c ，总存在 0x ，使得当   ，0xx ，恒有 xcex 2 . 21. 本题设有（1），（2），（3）三个选考题，每题 7 分，请考生任选 2 题作答，满分 14 分. 如果多做，则按所做的前两题计分.作答时，先用 2B 铅笔在答题卡上把所选题目对应题 号右边的方框涂黑，并将所选题号填入括号中. （1）（本小题满分 7 分）选修 4—2：矩阵与变换 已知矩阵 A 的逆矩阵       21 121A . （I）求矩阵 ； （II）求矩阵 1A 的特征值以及属于每个特征值的一个特征向量. （2）（本小题满分 7 分）选修 4—4：极坐标与参数方程 已知直线l 的参数方程为      ty tax 4 2 ，（ t 为参数），圆C 的参数方程为        sin4 cos4 y x ，（  为常数）. （I）求直线 和圆 的普通方程； （II）若直线 与圆 有公共点，求实数 a 的取值范围. （3）（本小题满分 7 分）选修 4—5：不等式选将 已知定义在 R 上的函数   21  xxxf 的最小值为 a . （I）求 的值； （II）若 rqp ，， 为正实数，且 arqp  ，求证： 3222  rqp .