高考数学模拟试卷3 (5) 16页

- 1 - 高考数学模拟训练题（第 41 套） 第Ⅰ卷 一、选择题：本大题共 12 小题，每小题 5 分，在每小题给出的四个选项中， 只有一项是符合题目要求的。 1．设集合 { | 1 1}A x x    ， 2{ | 0}B x x x   ，则 A B =（ ） A．{ | 1 0}x x   B．{ | 1 0x x   或 1}x  C．{ | 0 1}x x  D．{ | 0 1}x x  2．设复数 z 满足 2 +i + 2i iz  ，则 z  （ ） A．3 B． 10 C．9 D．10 3．已知实数 a ， b 满足：1 2 2a b  ，则（ ） A． 1 1 a b  B． 2 2log loga b C． a b D． cos cosa b 4．已知命题 :p 对任意 0x  ，总有sin x x ；命题 :q 直线 1 : 2 1 0l ax y   ，  2 : 1 1 0l x a y    ，若 1 2l l∥ ，则 2a  或 1a   ；则下列命题中是真命题的是（ ） A． p q B．   p q   C． p q  D． p q 5．在区域 0 1 0 1 x y        内任意取一点  ,P x y ，则 2 2 1x y  的概率是（ ） A． 2π 4 4  B． 4 π 4  C． π 2 4  D． π 4 6．将函数 πsin 6y x     的图象上所有的点向右平移 π 4 个单位长度，再把图象上各点的横坐 标扩大到原来的 2 倍(纵坐标不变)，则所得图象的解析式为（ ） A． 5πsin 2 12y x     B． πsin 2 12 xy      C． 5πsin 2 12 xy      D． 5πsin 2 24 xy      - 2 - 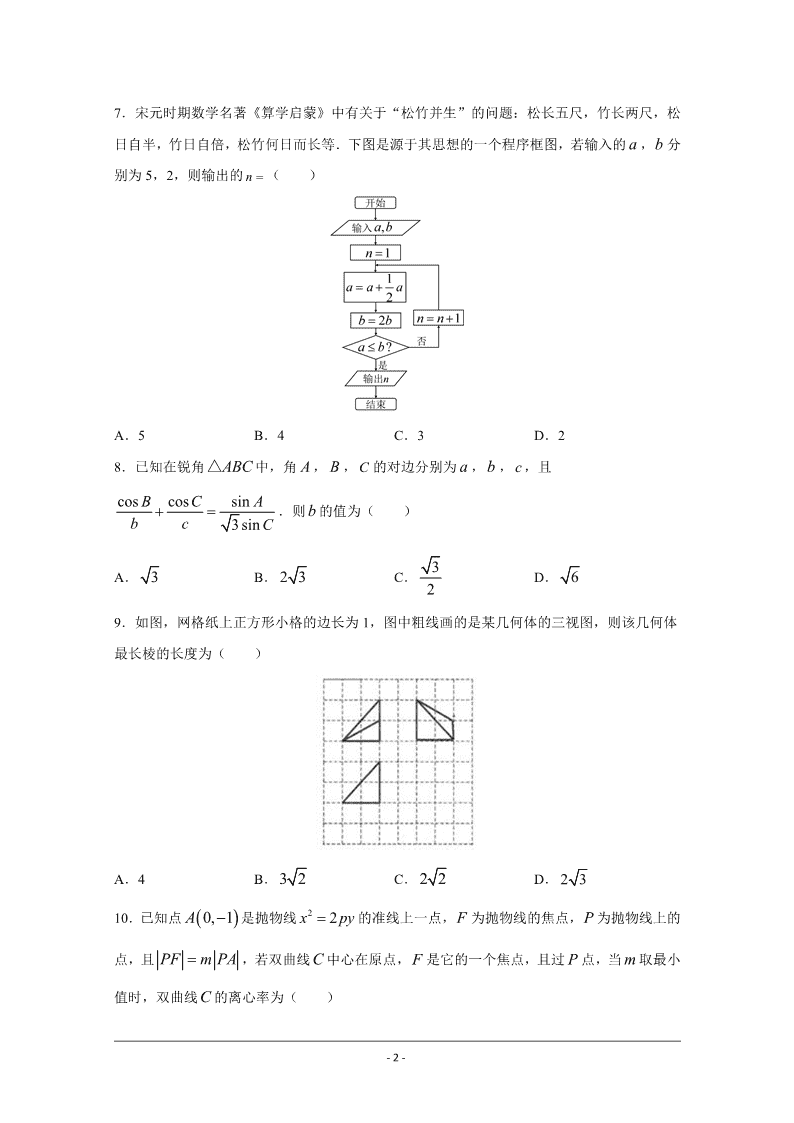7．宋元时期数学名著《算学启蒙》中有关于“松竹并生”的问题：松长五尺，竹长两尺，松 日自半，竹日自倍，松竹何日而长等．下图是源于其思想的一个程序框图，若输入的 a ，b 分 别为 5，2，则输出的 n  （ ） A．5 B．4 C．3 D．2 8．已知在锐角 ABC△ 中，角 A ， B ，C 的对边分别为 a ， b ， c ，且 cos cos sin 3sin B C A b c C   ．则b 的值为（ ） A． 3 B． 2 3 C． 3 2 D． 6 9．如图，网格纸上正方形小格的边长为 1，图中粗线画的是某几何体的三视图，则该几何体 最长棱的长度为（ ） A．4 B．3 2 C． 2 2 D． 2 3 10．已知点  0, 1A  是抛物线 2 2x py 的准线上一点，F 为抛物线的焦点，P 为抛物线上的 点，且 PF m PA ，若双曲线C 中心在原点，F 是它的一个焦点，且过 P 点，当 m 取最小 值时，双曲线 C 的离心率为（ ） - 3 - A． 2 B． 3 C． 2 1 D． 3 1 11．如图：在正方体 1 1 1 1ABCD A B C D 中，点 P 是 1B C 的中点，动点 M 在其表面上运动， 且与平面 1 1A DC 的距离保持不变，运行轨迹为 S ，当 M 从 P 点出发，绕其轨迹运行一周的过 程中，运动的路程 x 与 1 1l MA MC MD   之间满足函数关系  l f x ，则此函数图象大致 是（ ） A． B． C． D． 12．已知偶函数  f x 满足    4 4f x f x   ，且  0 0f  ，当  0,4x 时，    ln 2xf x x  ，关于 x 的不等式    2 0f x af x  在 200,200 上有且只有300个整数 解，则实数 a 的取值范围是（ ） A． 1ln2, ln63      B． 1ln2, ln63      C． 1 3ln2ln6,3 4      D． 1 3ln2ln6,3 4      13．已知平面向量 a ， b 的夹角为150 ，且 3a ， 2b ．则 2 a b ______________． 14．已知  π 32 π 2 cos sin dm x x x x    ，则 9 21 2 m x x     的展开式中，常数项为__________． 15．如图所示，正四面体 A B C D 中，E 是棱 A D 的中点，P 是棱 A C 上一动点， B P P E 的最 小值为 14 ，则该正四面体的外接球面积是__________． - 4 - 16．对于任一实数序列  1 2 3, , ,A a a a  ，定义 A 为序列 2 1 3 2 4 3, , ,a a a a a a    ，它 的第 n 项是 1n na a  ，假定序列  A  的所有项都是1，且 18 2017 0a a  ，则 2018a  _________． 三、解答题：解答应写出文字说明、证明过程或演算步骤。 17．数列 na 为正项数列， 1 4a  ，且对 *n N ，都有 2 2 1 12n n n na a a a   ； （1）求数列 na 的通项公式； （2）若数列 nb 满足 2 2 1 1 log logn n n b a a    ， nT 为数列 nb 的前项和，求证： 1nT  ． 18．2016 年微信用户数量统计显示，微信注册用户数量已经突破 9 .2 7 亿．微信用户平均年龄 只有 26 岁， 97.7% 的用户在50岁以下，86.2% 的用户在18 36 岁之间，为调查大学生这个微 信用户群体中每人拥有微信的数量，现在从北京大学生中随机抽取1 0 0 位同学进行了抽样调 查，结果如下： 微信群数量 频数 频率 0 至 5 个 0 0 6 至10个 30 0 .3 11至15个 30 0 .3 16至 20 个 a c 20 个以上 5 b 合计 1 0 0 1 （1）求 a ， b ， c 的值； （2）若从1 0 0 位同学中随机抽取 2 人，求这 2 人中恰有1 人微信群个数超过15个的概率； - 5 - （3）以这1 0 0 个人的样本数据估计北京市的总体数据且以频率估计概率，若从全市大学生．．．．．中 随机抽取 3 人，记 X 表示抽到的是微信群个数超过15个的人数，求 X 的分布列和数学期望 E X ． 19．如图，在四棱锥 A B C F E 中，四边形 EFCB 为梯形，EF BC∥ ，且 3 4EF BC ， ABC△ 是边长为 2 的正三角形，顶点 F 在 A C 上的射影为点G，且 3FG  ， 21 2CF  ， 5 2BF  ． （1）证明：平面 F G B  平面 A B C ； （2）求二面角 E A B F  的余弦值． 20．已知曲线 2 2 1 : 16 3 x yC   ，曲线 2 2 : 2 ( 0)C x py p  ，且 1C 与 2C 的焦点之间的距离为 2 ， 且 1C 与 2C 在第一象限的交点为 A ． （1）求曲线 2C 的方程和点 A 的坐标； （2）若过点 A 且斜率为  0k k  的直线l 与 1C 的另一个交点为 B ，过点 A 与l 垂直的直线与 2C 的另一个交点为C ．设 2 4 5 AB m AC    ，试求 m 取值范围． 21．已知   1 1e + lnef x x xx       ． （1）求函数  f x 的极值； （2）设    ln 1 exg x x ax    ，对于任意  1 0,x   ，  2 1,x   ，总有    1 2 e 2g x f x 成立，求实数 a 的取值范围． - 6 - 请考生在 22、23 题中任选一题作答,如果多做,则按所做的第一题计分。 22．已知曲线C 的参数方程为 1 2cos 1 2sin x y           （ 为参数）；直线 :l   （  0,   ， R ） 与曲线C 相交于 M ， N 两点，以极点O 为原点，极轴为 x 轴的负半轴建立平面直角坐标系． （1）求曲线C 的极坐标方程； （2）记线段 M N 的中点为 P ，若 OP  恒成立，求实数  的取值范围． 23．【选修 4—5：不等式选讲】 已知函数   2 4 1f x x x    ， （1）解不等式   9f x  ； （2）若不等式   2f x x a  的解集为 A ，  2 3 0 B x x x   ，且满足 B A ，求实数 a 的 取值范围． - 7 - 高考数学模拟训练题答案（第 41 套） 1【答案】A 【解析】由 2 0x x  得  2 1 0x x x x    ，解得 0x  ，或 1x  ，故  1,0A B   ． 故选 A． 2．【答案】A 【解析】      5 2i i2 i 2i 5 2i 2 5ii i i iz          ， 2 5i 4 5 3    ．故选 A． 3． 【答案】B 【解析】函数 2xy  为增函数，故 0b a  ．而对数函数 2logy x 为增函数，所以 2 2log loga b ，故选 B． 4．【答案】D 【解析】构造函数   sinf x x x  ，  0 0f  ，   1 cos 0f x x   ，故函数在 0, 上 单调递增，故   0f x  ，也即 sinx x ，故 p 为真命题．由于两直线平行，故  1 2 0a a    ， 解得 2a  或 1a   ，当 1a   时， 1l 与 2l 重合，故 q 为假命题．故 p q 为真命题．所以 选 D． 5． 【答案】B 【解析】画出图象如图阴影部分所示，故概率为 11 π 4 π4 1 4   ，所以选 B． 6． 【答案】C - 8 - 【解析】向右平移 π 4 个单位长度得带 5πsin 12x    ，再把图象上各点的横坐标扩大到原来的 2 倍(纵坐标不变)得到 5πsin 2 12 xy      ，故选 C． 7．【答案】B 【解析】模拟程序运行，可得： 5a  ， 2b  ， 1n  ， 15 2a  ， 4b  ，不满足条件 a b ，执行循环体； 2n  ， 45 4a  ， 8b  ，不满足条件 a b ，执行循环体； 3n  ， 135 8a  ， 16b  ，不满足条件 a b ，执行循环体； 4n  ， 405 16a  ， 32b  ，满足条件 a b ，退出循环，输出 n 的值为 4 ． 故选 B． 8．【答案】A 【解析】由正弦定理和余弦定理得 2 2 2 2 2 2 2 2 3 a c b a b c a abc abc c      ，化简得 3b  ． 9．【答案】D 【解析】如图所示，由三视图可知该几何体为：四棱锥 A B C D E ． 其中， AC  平面 B C D E ， 2A C C D D E   ， 1C B  ． ∴ 2 22 1 5AB    ， 2 22 1 5BE    ， 2 22 2 2 2AD    ，则  2 22 2 2 2 3AE    ．∴该几何体最长棱的长度 2 3 ．故选 D． 10．【答案】C 【解析】由于 A 在抛物线准线上，故 2p  ，故抛物线方程为 2 4x y ，焦点坐标为 0,1 ．当 直线 PA 和抛物线相切时， m 取得最小值，设直线 PA 的方程为 1y kx  ，代入抛物线方 程得 2 4 4 0x kx   ，判别式 216 16 0k    ，解得 1k   ，不妨设 1k  ，由 - 9 - 2 4 4 0x x   ， 解得 2x  ，即  2,1P ．设双曲线方程为 2 2 2 2 1y x a b   ，将 P 点坐标代入得 2 2 1 4 1a b   ， 即 2 2 2 24 0b a a b   ，而双曲线 1c  ，故 2 21 a b  ， 2 21b a  ，所以  2 2 2 21 4 1 0a a a a     ，解得 2 1a   ，故离心率为 1 2 1 2 1 c a     ，故选 C． 11．【答案】D 【解析】画出图象如图所示，由于平面 1B AC∥平面 1 1A DC ，故三角形 1AB C 即 M 点的运行 轨迹．以 D 为坐标原点建立空间直角坐标系，故  1 1,0,1A ，  1 0,1,1C ．当 M 在 1 1,1,2 2P     时， 0 23 2l   ，当 M 在  1 1,1,1B 时， 1 03 2l l   ，由此排除 A，C 两个选项．根 据图象的对称性可知，当 M 在 1PB 和 1B Q 上运动时，图象应该对称，故排除 B 选项．所以 选 D． 12．【答案】D 【解析】由    4 4f x f x   可知函数的对称轴为 4x  ，由于函数是偶函数， 0x  也 是它的对称轴，故函数是周期为 8 的周期函数．当  0,4x 时，   2 1 ln2xf x x   ，函数在 e0, 2      上递增，在 e ,42      上递增，最大值 e 2 2 ef      ，且   ln8 34 ln2 04 4f    ．由选项 可知 0a  ，所以     0f x f x a    ，解得   0f x  或  f x a  ．根据单调性和周期 性画出图象如图所示，由图可知   0f x  没有整数解．根据函数为偶函数，所以在  0,200 上 - 10 - 有 25 个周期，且有 150 个整数解，也即每个周期内有6 个解．   13 ln63f  ，故    4 3f a f   ， 解得 1 3ln2ln63 4x    ． 13【答案】2 【解析】  2 2 22 2 4 4 4 2        a b a b a a b b ． 14．【答案】 21 16  【解析】函数 3 siny x x  是奇函数，则  π 32 π 2 sin d 0x x x   ， 则   π π 2 2 π π 2 2 cos d = sin =2m x x x    ，据此可得： 9 921 1 2 2 m x x x x             ， 其展开式的通项公式为：     9 9 3 9 2 1 9 9 1 1C 1 C22 r r r r rr r rT x x x                  ， 展开式中的常数项满足 3r  ，即：   9 3 3 3 3 1 9 1 211 C2 16T          ． 15【答案】12π 【解析】把正四面体 A B C D 展开成如图所示的菱形 A B C D ，在菱形 A B C D 中，连结 B E ， 交 AC 于 P ，则 B E 的长即为 B P P E 的最小值，即 14BE  ． 如图， 120BC D   ， 30D C E   ．∴ 90B C E   ， 设 D E x ，则 2A B B C C D A D x    ． - 11 - ∴ 3CE x ，则 2 2 7 14BE BC CE x    ． ∴ 2x  ，即正四面体 A B C D 的棱长为 2 2 ． ∴该正四面体的外接球的半径为 6 2 2 34   ， ∴该正四面体的外接球的面积为  2 4π 3 12π  ，故答案为12π ． 16【答案】1000 【解析】依题意知 A 是公差为 1的等差数列，设其首项为 a ，通项为 nb ，则  1 1 1nb a n n a       ，于是       1 1 1 1 1 1 1 1 2 1 12 n n n k k k k k a a n a a a a a b a n                         1 2 11 2 n na n a      ．由于 18 2017 0a a  ，即 1 1 17 136 0 2016 2015 1008 0 a a a a           ， 解得 1016a   ， 1 17136a  ．故  2018 2016 201717136 2017 1016 10002a       ． 三、解答题：解答应写出文字说明、证明过程或演算步骤。 17． 【答案】（1） 12n na  ；（2）见解析． 【解析】（1）∵ 2 2 1 12n n n na a a a   ，∴ 2 2 1 1 2 0n n n na a a a    ， ∴  1 12 0n n n na a a a    ，∵数列 na 为正项数列， ∴ 1 2n na a  ，∴ na 是以 1 4a  为首项， 2 为公比的等比数列， ∴ 12n na  ． （2）  2 2 1 1 1 1 1 log log 1 1n n n b a a n n n n       ， 1 1 1 1 1 11 1 12 2 3 1 1nT n n n           ． 18． 【答案】（1） 35a  ， 1 20b  ， 7 20c  ；（2） 16 33 ；（3）见解析． 【解析】（ 1 ）由已知得 0 3 0 3 0 5 1 0 0a     ，解得 35a  ， 5 1 100 20b   ， 35 7 100 20c   ． - 12 - （ 2 ）记“ 2 人中恰有 1 人微信群个数超过 15个”为事件 A ， 则   1 1 40 60 2 100 C C 16 C 33P A   ． 所以， 2 人中恰有 1 人微信群个数超过 15个的概率为 16 33 ． （ 3 ）依题意可知，微信群个数超过 15个的概率为 2 5P  ． X 的所有可能取值 0 ， 1 ， 2 ， 3 ． 则   0 3 0 3 2 2 270 C 15 5 125P X               ，   1 2 1 3 2 2 541 C 15 5 125P X                ，   2 1 2 3 2 2 362 C 15 5 125P X                ，   3 0 3 3 2 2 83 C 15 5 125P X                ． 所以 X 的分布列为： X 0 1 2 3 P 27 125 54 125 36 125 8 125 数学期望 27 54 36 8 60 1 2 3125 125 125 125 5EX          ． 19． 【答案】（1）见解析；（2） 7 85 85 ． 【解析】（1）证明：由顶点 F 在 AC 上投影为点 G，可知， F G A C ． 取 AC 的中点为 O ，连结 O B ， G B ． 在 Rt FGC△ 中， 3FG  ， 21 2CF  ，所以 3 2CG  ． 在 Rt GBO△ 中， 3OB  ， 1 2OG  ，所以 13 2BG  ． 所以， 2 2 2BG G F FB  ，即 F G B G ． - 13 - ∵ FG AC ， FG GB ， AC BG G ，∴ FG  面 A B C ． 又 FG  面 F G B ，所以面 F G B  面 A B C ． （2）由（1）知， O B FG ， O B AC ，且 AC FG G ， 所以 OB  面 A F C ，且 FG  面 A B C ．以 O B 所在直线为 x 轴， OC 所在直线为 y 轴，过点 O 作平面 A B C 的垂线为 z 轴，建立空间直角坐标系，如图所示：  0, 1,0A  ，  3,0,0B ， 10, , 32F     ， 3 3 5, , 34 4E      ，  3, 1,0BA    ， 3 5, , 34 4BE         ， 13, , 32BF        ， 设平面 A B E ， A B F 的法向量分别为 m ， n ， 则 0 0 BA BE       m m   ，则  1, 3, 1  m ， 0 0 BA BF       n n   ，则 11, 3, 2      n ， 7 85cos 85   m n m n ， 所以二面角 E A B F  的余弦值为 7 85 85 ． 20．【答案】（1） 2 4x y ，  2,1A ；（2） 2 5 2 5( ,0) (0, )5 5m   ． 【解析】（1）曲线 1C 的焦点坐标为  3,0 ，曲线 2C 的焦点坐标为 0, 2 p     ，由 1C 与 2C 的 焦点之间的距离为 2，得 2 3 22 p     ，解得 2p  ，∴ 2C 的方程为 2 4x y ． 由 2 2 2 4 16 3 x y x y       ，解得  2,1A ． - 14 - （2）设直线 AB 的方程为  1 2y k x   ，即 2 1y kx k   ， 由 2 2 2 1 16 3 y kx k x y      ，得     222 1 4 1 2 2 1 2 6 0k x k k x k   ﹣ ﹣ ﹣ ． 则  2 2 2 1 2 6 2 1A B kx x k    ，∵ 2Ax  ，∴  2 2 1 2 3 2 1B kx k    ， 又直线 AC 的方程为  11 2y xk     ，即 1 2 1y xk k     ，由 2 1 2 1 4 y xk k x y        ， 得 2 4 84 0x xk k     ，则 84A Cx x k    ，∵ 2Ax  ，∴ 42Cx k    ， ∴  2 2 2 2 2 2 1 2 3 4 41 1 2 12 1 2 1B A k kAB k x x k kk k             ， 同理 2 21 1 41 1 4C AAC x xk k k                 ， 2 2 2 2 4 4 4 510 55 10 AB km kAC k        ， 0k  ， 2 20 5m   即 2 5 2 5( ,0) (0, )5 5m   ．∴综上所述： 2 5 2 5( ,0) (0, )5 5m   ． 21．【答案】（1）  f x 的极小值为 1 2 e ef       ，极大值为   2e ef  ；（2）  ,2 ． 【解析】（1）     2 2 11 ee + 1 ee 1 x x f x x x x          ， 0x  ． - 15 - 所以  f x 的极小值为 1 2 e ef       ，极大值为   2e ef  ． （2）由（1）可知当  1,x  时，函数  f x 的最大值为 2 e ， 对于任意  1 0,x   ，  2 1,x   ，总有    1 2 e 2g x f x 成立，等价于   1g x  恒成立，   1e 1 xg x ax     ． ① 2a  时，因为 e 1x x  ，所以   1 1e 1 2 01 1 xg x a x a ax x            ， 即  g x 在  0, 上单调递增，    0 1g x g  恒成立，符合题意． ②当 2a  时，设   1e 1 xh x ax    ，         2 2 2 1 e 11e 0 1 1 x x xh x x x         ， 所以  g x 在  0, 上单调递增，且  0 2 0g a   ，则存在  0 0,x   ，使得   0g x  ， 所以  g x 在 00, x 上单调递减，在 0,x  上单调递增，又    0 0 1g x g  ， 所以   1g x  不恒成立，不合题意． 综合①②可知，所求实数 a 的取值范围是 ,2 ． 请考生在 22、23 题中任选一题作答,如果多做,则按所做的第一题计分。 22． 【答案】（1） 2 2 2 cos 24          ；（2） 2,  ． 【解析】（1）∵曲线 C 的参数方程为 1 2cos 1 2sin x y           （  为参数）， ∴所求方程为    2 2 21 1 2x y    ， ∵ cos sin x y          ，∴ 2 2 cos 2 sin 2       ， - 16 - ∴曲线 C 的极坐标方程为 2 π2 2 cos 24         ． （2）联立   和 2 2 cos 2 sin 2 0        ，得  2 2 cos sin 2 0       ， 设  1,M   、  2,N   ，则  1 2 π2 sin cos 2 2sin 4             ， 由 1 2 2OP   ，得 π2 sin 24OP       ， 当 3π 4   时， OP 取最大值 2 ，故实数  的取值范围为 2,  ． 23．【答案】（1）  2,4 ；（2） 5a  ． 【解析】（1）   9f x  可化为 2 4 1 9x x    ， 2 3 3 9 x x       ，或 1 2 5 9 x x         ，或 1 3 3 9 x x         ； 2 4x  ，或 1 2x   ，或 2 1x    ； 不等式的解集为  2,4 ． （2）易知  0,3B  ，所以 B A ， 所以 2 4 1 2x x x a     在  0,3x 恒成立； 2 4 1x x a     在  0,3x 恒成立； 1 2 4 1x a x x a         在  0,3x 恒成立；     3 0,3 3 5 0,3 a x x a x x         在 恒成立 在 恒成立 0 55 a aa       ．