2012年江苏省海门市初三一模数学调研考试 12页

‎2012年江苏省海门市初三一模调研考试 数 学 注意事项 考生在答题前请认真阅读注意事项：‎ 1. 本试卷共6页，满分为150分，考试时间为120分钟，考试结束后，请将本试卷和答题卡一并交回．‎ 2. 答题前，请务必将自己的姓名、考试证号用0.5毫米黑色字迹的签字笔填写在试卷及答题卡上指定的位置．‎ 3. 答案必须按要求填涂、书写在答题卡上，在试卷、草稿纸上答题一律无效．‎ 一、选择题（本大题共10小题，每小题2分，共30分，在每小题给出的四个选项中，恰 有一项是符合题目要求的，请将正确选项的字母代号填涂在答题卡相应位置上）‎ ‎ 1．计算的值为（ ▲ ）‎ A．±4 B．±‎2 ‎ C．4 D．2‎ ‎ 2．观察下列图案，其中既是轴对称图形又是中心对称图形的有（ ▲ ）‎ ‎ ‎ ‎ A．1个 B．2个 C．3个 D．4个 ‎ 3．如图所示，下列选项中，正六棱柱的左视图是（ ▲ ）‎ ‎ ‎ ‎ A B C D ‎ 4．一只盒子中有红球m个，白球8个，黑球n个，每个球除颜色外都相同，从中任取一 个球，取得白球的概率与不是白球的概率相同，那么m与n的关系是（ ▲ ）‎ A．m=3，n=5 B．m=n=‎4 ‎ C．m+n=4 D．m+n=8‎ ‎ 5．下列调查中，适合采用全面调查（普查）方式的是（ ▲ ） ‎ A．对长江水质情况的调查 ‎ B．对端午节期间市场上粽子质量情况的调查 C．对某通信卫星的零部件的质量情况的调查 ‎ D．对某类烟花爆竹燃放安全情况的调查 ‎ 6．已知圆锥的侧面积为cm2，侧面展开图的圆心角为45°，则该圆锥的母线长为 ‎ ‎ （ ▲ ）‎ A．‎64cm B．‎8cm　　　　　C． cm D．cm ‎ 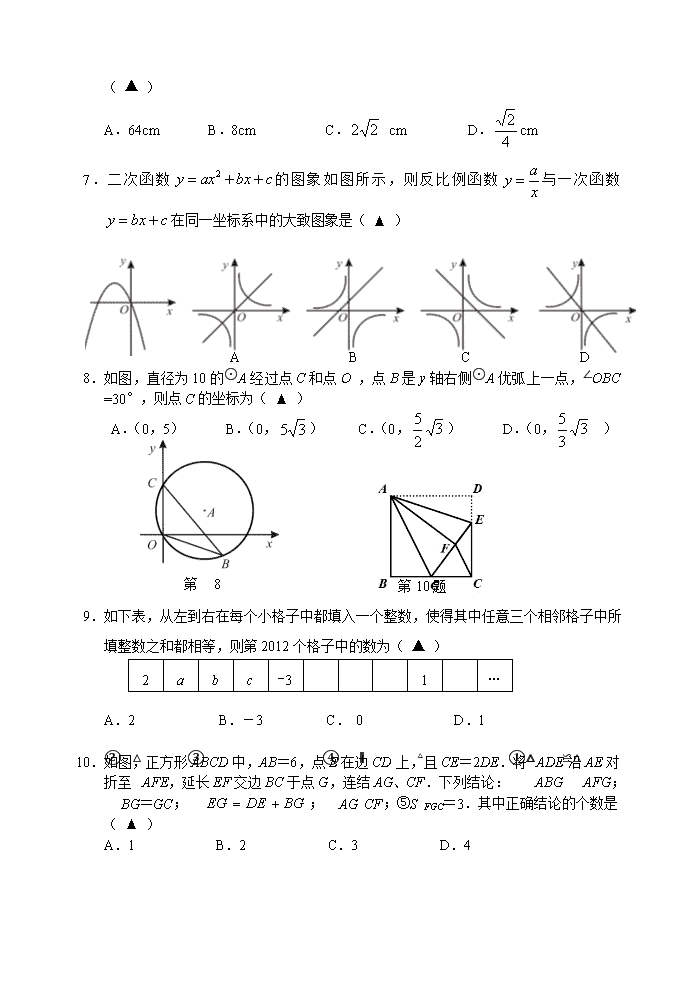7．二次函数的图象如图所示，则反比例函数与一次函数 在同一坐标系中的大致图象是（ ▲ ）‎ ‎ A B C D ‎ 8．如图，直径为10的⊙A经过点C和点O ，点B是y轴右侧⊙A优弧上一点，∠OBC =30°，则点C的坐标为（ ▲ ）‎ ‎ A．（0，5） B．（0，） C．（0，） D．（0，）‎ ‎ ‎ 第10题 第8题 ‎ 9．如下表，从左到右在每个小格子中都填入一个整数，使得其中任意三个相邻格子中所填整数之和都相等，则第2012个格子中的数为（ ▲ ） ‎ ‎2‎ a b c ‎-3‎ ‎1‎ ‎…‎ A．2 B．－‎3 C． 0 D．1‎ ‎10．如图，正方形ABCD中，AB＝6，点E在边CD上，且CE＝2DE．将△ADE沿AE对折至△AFE，延长EF交边BC于点G，连结AG、CF．下列结论：①△ABG≌△AFG；②BG＝GC；③；④AG∥CF；⑤S△FGC＝3．其中正确结论的个数是（ ▲ ）‎ A．1 B．‎2 ‎ C．3 D．4‎ 二、填空题：本大题共8小题，每小题3分，共24分．不需写出解答过程，请把答案直接填写在答题卡相应位置上．‎ ‎11．地球上的海洋面积约为‎361000000km2，用科学记数法可表示为 ▲ km2． ‎ ‎12．分解因式： ▲ ．‎ ‎13．乐乐和爸爸到广场散步，爸爸的身高是‎176cm，乐乐的身高是‎156cm，在同一时刻爸 爸的影长是‎44cm，那么乐乐的影长是 ▲ cm．‎ ‎14．如图，D是AB边上的中点，将沿过D的直线折叠，使点A落在BC上F处，若，则 ▲ 度．‎ ‎15．如图，AB是⊙O的直径，PA切⊙O于A，OP交⊙O于C，连BC．若∠P=30°，则 ‎∠B= ▲ °．‎ ‎16．一组数据0，5，3，的平均数是1，则这组数据的中位数是 ▲ ．‎ y O x C A(1，2)‎ B(m，n)‎ ‎17．如图，在平面直角坐标系中，函数（x>0，常数k >0）的图象经过点A（1，2）， B（m，n）（m>1），过点B作y轴的垂线，垂足为C．若△ABC的面积为2，则 点B的坐标为 ▲ ．‎A B C P O 第16题 第14题 ‎ 第17题 ‎18．如图，矩形ABCD中，AB=4，BC=8，E为CD的中点，点P、Q为BC上两个动点，且PQ=3，当CQ= ▲ 时，四边形APQE的周长最小．‎ 第18题 三、解答题（本大题共10小题，共96分．请在答题卡指定区域内作答，解答时应写出必要的文字说明、证明过程或演算步骤）‎ ‎19．（本小题满分10分）‎ ‎（1）计算：；‎ ‎（2）先化简，再求值：．‎ ‎20．（本小题满分7分）‎ 如图，在边长为1个单位长度的小正方形组成的网格中，按要求画出△A1B1C1和 △A2B2C2；‎ ‎（1）以O为位似中心，在点O的同侧作△A1B1C1， 使得它与原三角形的位似比为1：2；‎ A B O ‎（2）将△ABC绕点O顺时针旋转90°得到△ A2B‎2C2，并求出点A旋转的路径的长．‎ ‎（第20题）‎ ‎21．（本小题满分8分）‎ 为了了解我县初中学生体育活动情况，随机调查了720名八年级学生，调查内容是： “每天锻炼是否超过1小时及未超过1小时的原因”，利用所得的数据制成了扇形统 计图和频数分布直方图．根据图示，解答下列问题：‎ ‎（1）若在被调查的学生中随机选出一名学生测试其体育成绩，选出的是“每天锻炼 超过1小时”的学生的概率是多少？‎ ‎（2）“没时间”锻炼的人数是多少？并补全频数分布直方图；‎ 人数 ‎50‎ ‎150‎ ‎100‎ ‎200‎ ‎250‎ ‎300‎ ‎350‎ ‎400‎ ‎450‎ ‎0‎ 不喜欢 没时间 其他 原因 锻炼未超过1小时频数分布图 ‎120‎ ‎20‎ ‎（3）2012年我县八年级学生约为1.2万人，按此调查，可以估计2012年我县八年级 学生中每天锻炼未超过1小时的学生约有多少万人？‎ ‎22．（本小题满分9分）‎ 关于x的方程有两个不相等的实数根．‎ ‎（1）求k的取值范围；‎ ‎（2）设方程的两根分别为，若，求k的值． ‎ ‎23．（本小题满分8分）‎ 如图，在△ABC，AB=AC，以AB为直径的⊙O分别交AC、BC于点D、 E，点F在 AC的延长线上，且．‎ ‎（1）求证：直线BF是⊙O的切线；‎ ‎（2）若AB=6，BF=8，求．‎ ‎24．（本小题满分8分）‎ 小明和小颖做掷骰子的游戏，规则如下：‎ ‎（第23题）‎ ‎①游戏前，每人选一个数字；‎ ‎②每次同时掷两枚均匀骰子；‎ ‎③如果同时掷得的两枚骰子点数之和，与谁所选数字相同，那么谁就获胜．‎ ‎（1）用列表法或树状图列出同时掷两枚均匀骰子所有可能出现的结果：‎ ‎（2）小明选的数字是5，小颖选的数字是6．如果你也加入游戏，你会选什么数字， 使自己获胜的概率比他们大？请说明理由．‎ ‎25．（本小题满分10分）‎ 已知二次函数的图像经过点A（，9），B（0，3）和点C（4，3）． （1）求该二次函数的关系式，并求出它的顶点M的坐标；‎ ‎（2）若两点都在该函数的图象上，试比较与的大小．‎ ‎26．（本小题满分10分）‎ 如图，唐诗同学正在操场上放风筝，风筝从A处起飞，几分钟后便飞达C处，此时， 在AQ延长线上B处的宋词同学，发现自己的位置与风筝和旗杆PQ的顶点P在同一 直线上．‎ ‎（1）已知旗杆高为10米，若在B处测得旗杆顶点P的仰角为30°，A处测得点P的 仰角为45°，试求A、B之间的距离；‎ BA A DA CDA PCDA QPCDA ‎（2）此时，在A处又测得风筝的仰角为75°，若绳子在空中视为一条线段，绳子AC 约为多少？（结果可保留根号）‎ ‎（第26题）‎ ‎ 27．（本小题满分12分）‎ 两个全等的直角三角形ABC和DEF重叠在一起，其中∠A=60°，AC=1．固定△ABC 不动，将△DEF进行如下操作：‎ ‎ （1）如图（1），△DEF沿线段AB向右平移（即D点在线段AB内移动），连结DC、 CF、FB，四边形CDBF的形状在不断的变化，它的面积是否变化，如果不变请求出 其面积．如果变化，说明理由．‎ A B E F C D 图（2）‎ A B E F C D 图（1）‎ ‎（2）如图（2），当D点移到AB的中点时，请你猜想四边形CDBF的形状，并说明 理由．‎ A B ‎(E)‎ ‎(F)‎ C D 图（3）‎ E ‎(F)‎ （3） 如图（3），△DEF的D点固定在AB的 中点，然后绕D点按顺时针方向旋转△DEF，‎ 使DF落在AB边上，此时F点恰好与B点重 合，连结AE，请你求出的值．‎ ‎28．（本小题满分14分）‎ 如图，直角梯形OABC中，AB∥OC，O为坐标原点，点A在y轴正半轴上，点C 在x轴正半轴上，点B坐标为（2，2），∠BCO= 60°，于点E．动点P 从点E出发，沿线段EO向点O运动，动点Q从点O出发，沿线段OA向点A运动， 两点同时出发，速度都为每秒1个单位长度．设点P运动的时间为t秒．‎ ‎（1）求OE的长；‎ E ‎（2）若△OPQ的面积为S（平方单位），求S与t之间的函数关系式．并求t为何值时，△OPQ的面积最大，最大值是多少？‎ ‎（3）设PQ与OB交于点M．①当△OPM为等腰三角形时，求（2）中S的值．‎ ‎（第28题）‎ ‎ ②探究线段OM长度的最大值是多少，直接写出结论．‎ 数学参考答案 一、 选择题 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ 选项 C B B D C B D A B D 二、填空题 ‎11．； 12．； 13．39； 14．80； ‎ ‎15．30； 16．； 17．； 18．．‎ 三、 解答题 1. ‎（1）‎ 原式 ……………… 4分 ‎ ………………5分 ‎（2）‎ 解：原式 ………………2分 ‎ ……………… 4分 当时，原式 ……………… 5分 2. ‎（1）作图略； ………………2分 ‎（2）作图 ………………4分 ‎∵ ……………… 5分 ‎∴点A运动的路径为弧的长………………7分 ‎21．解（1） ………………2分 ‎（2）720×－120－20=400 ………………4分 ‎“没时间”锻炼的人数是400名．………………6分 ‎（3）1.2×=0.9（万人）‎ ‎∴估计2011年我县八年级学生中每天锻炼未超过1小时的学生约有0.9万人．……8分 （3） 解：（1）由题意可得 ‎ ………………2分 ‎∴‎ ‎∴‎ ‎∴且 ………………4分 （2） 由题意可得 ‎ ………………5分 ‎∵‎ ‎∴‎ ‎∴或 ………………7分 解得或 经检验，是上述方程的根 ………………8分 ‎∵且 ‎ ‎∴或 ……………… 9分 23． ‎（1）证明：连接AE ………………1分 ‎∵AB为⊙O的直径，‎ G ‎∴∠AEB=90°‎ ‎∴∠BAE+∠ABE=90°‎ ‎∵AB=AC，AE⊥BC ‎∴AE平分∠BAC ‎∴‎ ‎∴‎ ‎∴AB⊥BF ‎∴BF为⊙O的切线 ……………… 3分 （2） 过点C作CG⊥BF 在Rt△ABF中 ‎∵AC=6‎ ‎∴CF=4 ………………4分 ‎∵CG⊥BF，AB⊥BF ‎∴CG∥AB ‎∴△CFG∽△AFB ………………6分 ‎∴‎ ‎∴‎ ‎∴………………7分 在Rt△BCG中 ‎ ………………8分 ‎24．解：（1）略 ………………3分 ‎ （2）由上表可以看出，同时投掷两枚骰子，可能出现的结果有36种，它们出现的可能性相同．‎ ‎ 所有的结果中，满足两枚骰子点数和为5（记为事件）的结果有4种，即（1，4）， ‎ ‎ （2，3），（3，2）（4，1），所以小明获胜的概率为；…………… 4分 ‎ 满足两枚骰子点数和为6（记为事件）的结果有5种，即（1，5），（2，4），（3，3）‎ ‎ （4，2），（5，1），所以小颖获胜的概率为； ………………5分 要想使自己获胜的概率比他们大，必须满足两枚骰子点数和出现的结果多于5种，由所 列表格可知，只有两枚骰子点数和为7（记为事件）的结果多于5种，有6种，‎ 即（1，6），（2，5），（3，4）（4，3），（5，2），（6，1），所以．‎ 因此，要想使自己获胜的概率比他们大，所选数字应为7．……………… 8分 25． 解：（1）根据题意可得 ‎ ………………2分 ‎ 解得 ……………… 3分 ‎ ∴该二次函数关系式为．………………4分 ‎ ∴ ∴此抛物线的顶点M为（2，1）……………5分 ‎（2）∵两点都在函数的图象上，‎ ‎ ∴，．‎ ‎ ∴ ………………7分 ‎ ∴当时，即时，；‎ ‎ 当时，即时，；‎ ‎ 当时，即时，．………………10分 ‎26．解(1) 在Rt△BPQ中，PQ=‎10米，∠B=30°， ‎ 则BQ=cot30°×PQ＝ ………………2分 又在Rt△APQ中，∠PAB=45°，‎ 则AQ=cot45°×PQ=10， ‎ 即：AB=(+10)(米)；……………… 5分 ‎(2) 过A作AE⊥BC于E，‎ 在Rt△ABE中，∠B=30°，AB=+10，‎ ‎∴ AE=sin30°×AB=（+10）=5+5，………………7分 ‎∵∠CAD=75°，∠B=30°，‎ ‎∴ ∠C=45°， ………………8分 在Rt△CAE中，sin45°＝，‎ ‎∴AC=（5+5）=(5+5)(米)………………10分 A B E F C D 图（1）‎ G 27． 解：（1）解：不变 ………………1分 过C点作CG⊥AB于G，‎ ‎ 在Rt△AGC中，∵sin60°=，∴‎ ‎∵AB=2，∴S梯形CDBF=S△ABC=………4分 ‎ （2）菱形………………5分 A B ‎(E)‎ ‎(F)‎ C D 图（3）‎ E ‎(F)‎ C H ‎∵CD∥BF， FC∥BD，‎ ‎∴四边形CDBF是平行四边形………………6分 ‎∵DF∥AC，∠ACD=90°，‎ ‎∴CB⊥DF ∴四边形CDBF是菱形………8分 ‎ (3)解法一：过D点作DH⊥AE于H，‎ 则S△ADE=‎ ‎ 又S△ADE=，‎ ‎ ∴在Rt△DHE’中，sinα= ………………12分 ‎ 解法二：∵△ADH∽△ABE 即： ‎ ‎ ∴ ∴sinα= ‎ ‎28．解：（1）∵∥‎ ‎ ∴ ‎ ‎ 在中， ,‎ ‎ ∴， ‎ ‎∴ 而 ‎ ∴为等边三角形 ‎ ∴………3分 ‎（2）∵‎ ‎∴ ‎ ‎∴‎ ‎= （）…………………………6分 即 ‎∴当时，………………………………………8分 ‎（3）①若为等腰三角形，则：‎ ‎（i）若， ‎ ‎ ∴∥ ‎ ‎∴ 即 解得：‎ 此时………………………………10分 ‎（ii）若，‎ ‎ ∴‎ 过点作，垂足为，则有：‎ 即 解得：‎ 此时……………………………………11分 ‎（iii）若，‎ ‎∴∥‎ 此时在上，不满足题意.……………………………………………12分 ‎ ②线段长的最大值为……………………………………14分 α