苏教版数学八年级上册课件1-3探索三角形全等的条件（2）ASA 11页

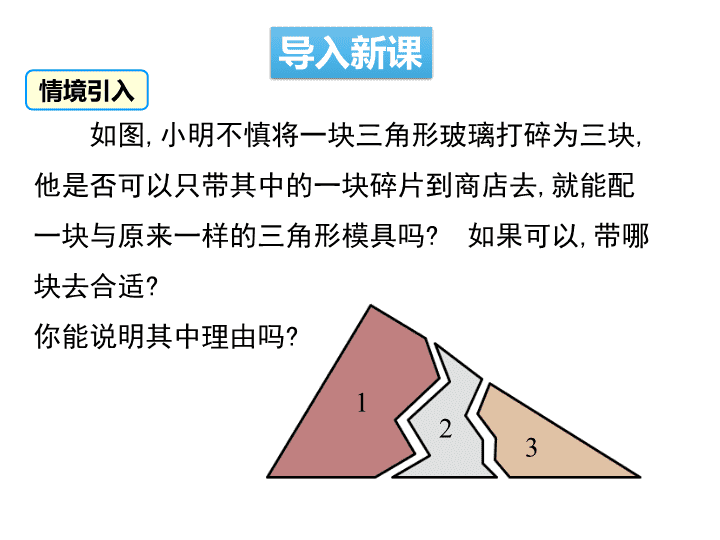
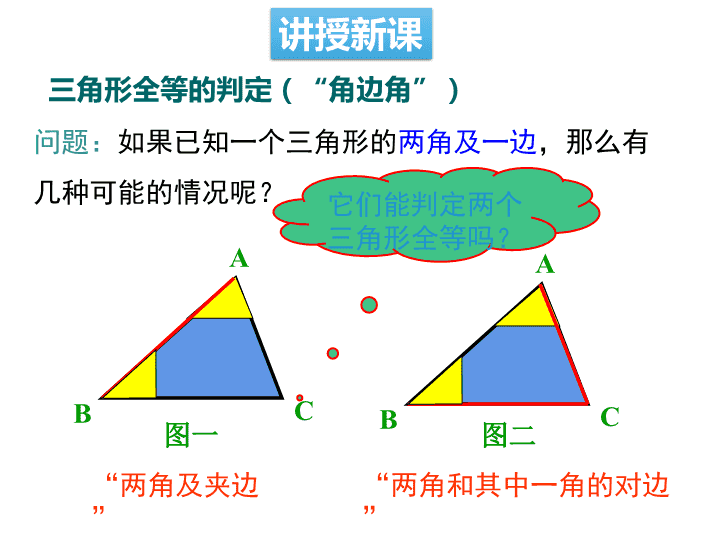
1.3探索三角形全等的条件（2） 如图,小明不慎将一块三角形玻璃打碎为三块, 他是否可以只带其中的一块碎片到商店去,就能配 一块与原来一样的三角形模具吗? 如果可以,带哪 块去合适? 你能说明其中理由吗? 情境引入 3 2 1 导入新课 三角形全等的判定（“角边角”） 问题：如果已知一个三角形的两角及一边，那么有 几种可能的情况呢？ A B C A B C 图一 图二 “两角及夹边” “两角和其中一角的对边” 它们能判定两个 三角形全等吗？ 讲授新课 作图探究 先任意画出一个△ABC，再画一个△A ′ B ′ C ′ ， 使A ′ B ′ =AB， ∠A ′ =∠A， ∠B ′ =∠B (即使两角和 它们的夹边对应相等).把画好的△A ′ B ′ C ′剪下，放到 △ABC上，它们全等吗？ A C B A C B A′ B′ C′ E D 作法： （1）画A'B'=AB; （2）在A'B'的同旁画∠DA'B '=∠A，∠EB'A '=∠B， A'D，B'E相交于点C'. 想一想：从中你能发现什么规律？ “角边角”判定方法 u文字语言：两角及其夹边分别相等的两个三角形 全等(简写成“角边角”或“ASA”）. u几何语言： ∠A=∠A′ （已知）， AB=A′ B′ （已知）， ∠B=∠B′ （已知）， 在△ABC和△A′ B′ C′中， ∴ △ABC≌△ A′ B′ C′ （ASA）. A B C A ′ B ′ C ′ 例1 已知：∠ABC＝∠DCB，∠ACB＝ ∠DBC， 试说明：△ABC≌△DCB． ∠ABC＝∠DCB(已知）， BC＝CB（公共边）， ∠ACB＝∠DBC（已知）， 解： 在△ABC和△DCB中， ∴△ABC≌△DCB（ASA ）. 典例精析 B C A D 判定方法：两角和它们的夹边对应相等两个三角形全等． 例2 如图，点D在AB上，点E在AC上，AB=AC, ∠B=∠C,试说明：AD=AE. A B C D E 分析：证明△ACD≌△ABE,就可以得出AD=AE. 解：在△ACD和△ABE中， ∠A=∠A（公共角 ）， AC=AB（已知）， ∠C=∠B （已知 ）， ∴ △ACD≌△ABE（ASA)， ∴AD=AE. 学以致用：如图,小明不慎将一块三角形模具打碎 为三块,他是否可以只带其中的一块碎片到商店去, 就能配一块与原来一样的三角形模具吗? 如果可 以,带哪块去合适?你能说明其中理由吗? 32 1 答：带1去，因为有两角且 夹边相等的两个三角形全等. 如图,已知AB∥DF,AC∥DE,BC=FE,且点 B,E,C,F在一条直线上.求证:△ABC≌ △DFE. 角 边 角 内 容 两角及其夹边分别相等的两个三 角形全等（简写成 “ASA”) 应 用 为证明线段和角相等提供了新的证法 注 意 注意夹边 课堂小结