第十九章《四边形》测试题-新人教 5页

第十九章《四边形》测试题 一、选择题 1．能判定四边形 ABCD 为平行四边形的题设是（ ）． （A）AB∥CD，AD=BC;（B）∠A=∠B，∠C=∠D; （C）AB=CD，AD=BC;（D）AB=AD，CB=CD 2．在给定的条件中，能画出平行四边形的是（ ）． （A）以 60cm 为一条对角线，20cm、34cm 为两条邻边; （B）以 6cm、10cm 为对角线，8cm 为一边; （C）以 20cm、36cm 为对角线，22cm 为一边; （D）以 6cm 为一条对角线，3cm、10cm 为两条邻边 3．正方形具有而菱形不一定具有的性质是（ ） （A）对角线互相平分;（B）对角线相等; （C）对角线平分一组对角;（D）对角线互相垂直 4．在下列说法中不正确的是（ ） （A）两条对角线互相垂直的矩形是正方形; （B）两条对角线相等的菱形是正方形; （C）两条对角线垂直且相等的平行四边形是正方形; （D）两条对角线垂直且相等的四边形是正方形 5．下列说法不正确的是（ ） （A）对角线相等且互相平分的四边形是矩形; （B）对角线互相垂直平分的四边形是菱形; （C）一组对边平行且不等的四边形是梯形; （D）一边上的两角相等的梯形是等腰梯形 6．不能判定四边形 ABCD 为平行四边形的题设是（ ） （A）AB=CD，AD=BC （B）AB // CD （C）AB=CD，AD∥BC （D）AB∥CD，AD∥BC 7．四边形 ABCD 的对角线 AC，BD 相交于点 O，能判定它为正方形的题设是（ ） （A）AO=CO，BO=DO;（B）AO=CO=BO=DO; （C）AO=CO，BO=DO，AC⊥BD; （D）AO=BO=CO=DO，AC⊥BD 8．下列说法不正确的是（ ） （A）只有一组对边平行的四边形是梯形; （B）只有一组对边相等的梯形是等腰梯形; （C）等腰梯形的对角线相等且互相平分; （D）在直角梯形中有且只有两个角是直角 9．如图 1，在ABCD 中，MN 分别是 AB、CD 的中点，BD 分别交 AN、CM 于点 P、Q，在结 论： ①DP=PQ=QB ②AP=CQ ③CQ=2MQ ④S△ADP= 1 4 S ABCD 中，正确的个数为（ ）． （A）1 （B）2 （C）3 （D）4 (1) (2) (3) 10．如图 2，在梯形 ABCD 中，AD∥CB，AD=2，BC=8，AC=6，BD=8，则梯形 ABCD 的面积为 （ ）． （A）24 （B）20 （C）16 （D）12 二、填空题 11．在ABCD 中，AC 与 BD 交于 O，则其中共有_____对全等的三角形． 12．矩形的对角线相交成的角中，有一个角是 60°，这个角所对的边长为 20cm，则其对 角线长为_______，矩形的面积为________． 13．一个菱形的两条对角线长分别为 6cm，8cm，这个菱形的边长为_______，面积 S=______． 14．如果一个四边形的四个角的比是 3：5：5：7，则这个四边形是_____形． 15．如图 3，等腰梯形 ABCD 中，AD∥BC，AB∥DE，BC=8，AB=6，AD=5，则△CDE 的周长是 ________． 16．如图 4，在正方形 ABCD 的外侧，作等边△ADE，则∠AEB=_______． (4) (5) (6) 17．在长为 1.6m，宽为 1.2m 的矩形铅板上，剪切如图 5 所示的直角梯形零件（尺寸单位 为 mm），则这块铅板最多能剪出______个这样的零件． 18．如图 6，ABCD 中，过对角线交点 O，引一直线交 BC 于 E，交 AD 于 F，若 AB=2.4cm， BC=4cm，OE=1.1cm，则四边形 CDFE 周长为________． 19．已知等腰梯形的一个锐角等于 60°，它两底分别为 15cm，49cm，则腰长为_______． 20．已知等腰梯形 ABCD 中 AD∥BC，BD 平分∠ABC，BD⊥DC，且梯形 ABCD的周长为 30cm， 则 AD=_____． 三、计算题 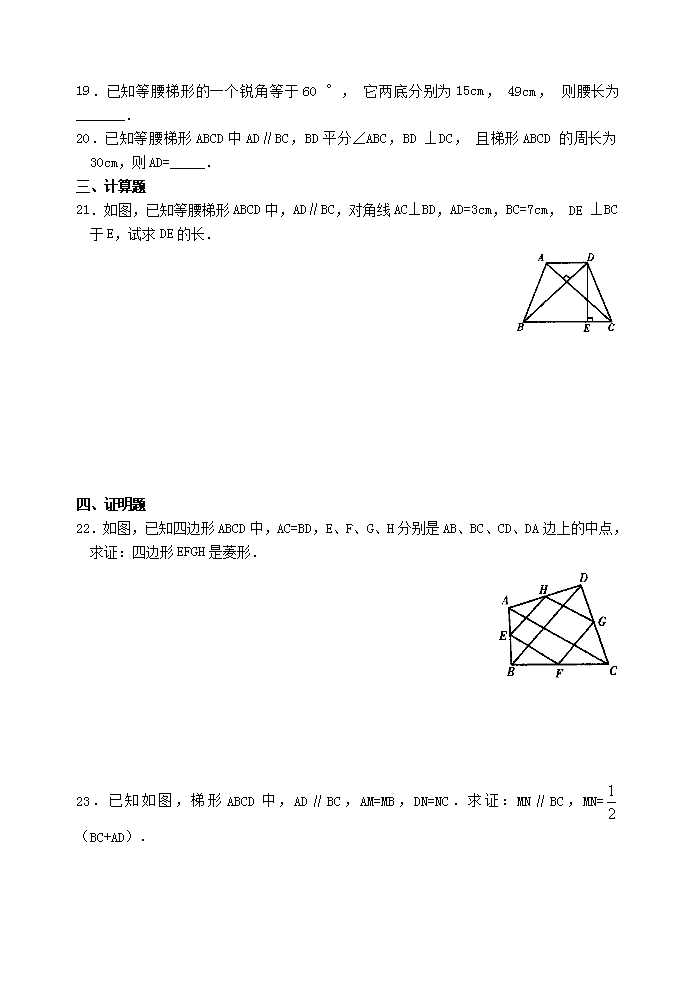21．如图，已知等腰梯形 ABCD 中，AD∥BC，对角线 AC⊥BD，AD=3cm，BC=7cm，DE⊥BC 于 E，试求 DE 的长． 四、证明题 22．如图，已知四边形 ABCD 中，AC=BD，E、F、G、H 分别是 AB、BC、CD、DA 边上的中点， 求证：四边形 EFGH 是菱形． 23．已知如图，梯形 ABCD 中，AD∥BC，AM=MB，DN=NC．求证：MN∥BC，MN= 1 2 （BC+AD）． 答案: 1．（C） 2．（C） 3．（B） 4．（D） 5．（D） 6．（C） 7．（D） 8．（C） 9．（C） 10．（A） 11．4 12．40cm400 3 cm2 13．5cm24cm2 14．直角梯形 15．15 16．15° 17．12 18．8.6cm 19．34cm 20．如图，作 AE⊥BC 于 E，DF⊥BC 于 F， ∴AD=EF，设 BE=x． 则 AB=2x，DC=2x，FC=x， ∴BD 平分∠ABC，∴∠DBC=30°． ∴DC= 1 2 BC，∴BC=4x． ∴EF=2x=AD． 又∵AB+BC+CD+AD=30， ∴4x+6x=30，x=3，∴AD=6（cm）． 21．过 D 点作 DF∥AC，交 BC 的延长线于点 F， 则四边形 ACFD 为平行四边形， 所以 AC=DF，AD=CF． 因为四边形 ABCD 为等腰梯形，所以 AC=BD， 所以 BD=DF，又已知 AC⊥BD，DF∥AC， 所以 BD⊥DF，则△BDF 为等腰直角三角形． 又因为 DF⊥BC，所以 DE= 1 2 BF= 1 2 （BC+CF）= 1 2 （BC+AD）= 1 2 （7+3）=5（cm）． 22．证明：∵E、F、G、H 分别是 AB、BC、CD、DA 的中点， ∴EF= 1 2 AC，HG= 1 2 AC，FG= 1 2 BD，EH= 1 2 BD． ∴EF=HG= 1 2 AC，FG=EH= 1 2 BD． 又∵AC=BD，∴EF=HG=FG=EH． ∴四边形 EFGH 是菱形． 23．证明：如图，连接 AN 并延长，交 BC 的延长线于点 E． ∵DN=NC，∠1=∠2，∠D=∠3， ∴△ADN≌△ECN， ∴AN=EN，AD=EC． 又 AM=MB，∴MN 是△ABE 的中位线． ∴MN∥BC，MN= 1 2 BE（三角形中位线定理） ∵BE=BC+CE=BC+AD， ∴MN= 1 2 （BC+AD）．