高考立体几何大题理科 10页

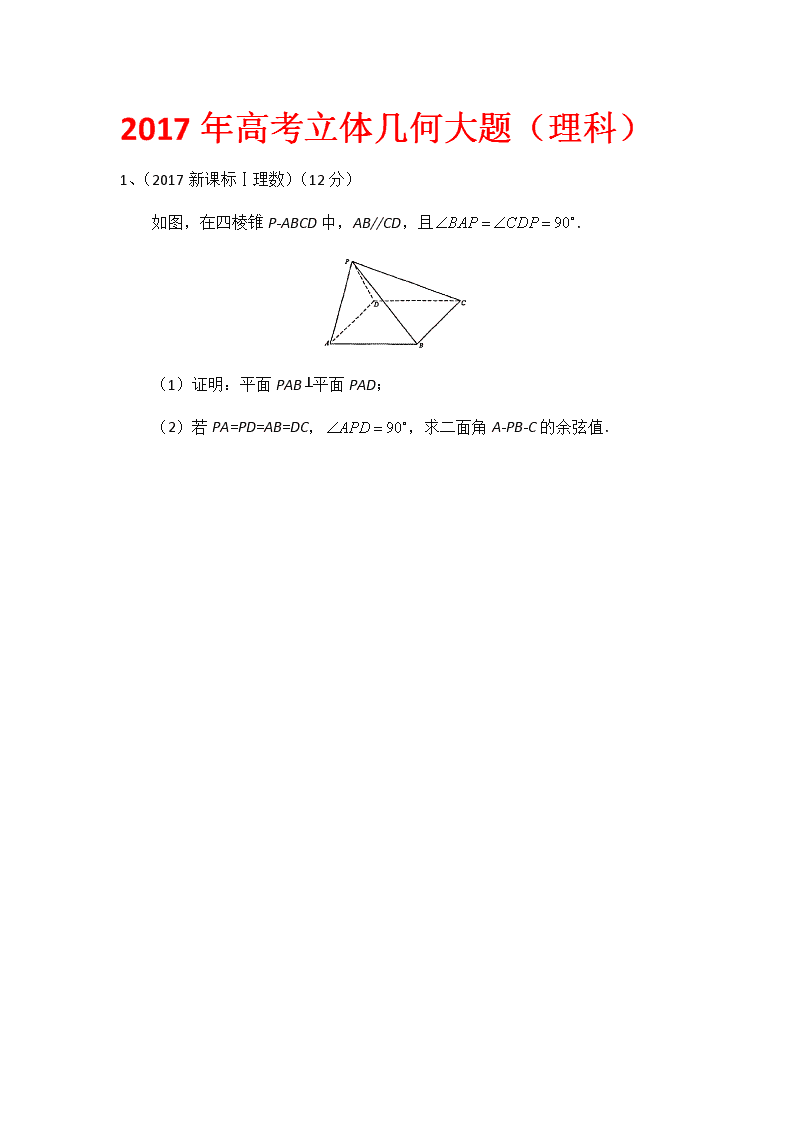
‎2017年高考立体几何大题（理科）‎ ‎1、（2017新课标Ⅰ理数）（12分）‎ 如图，在四棱锥P-ABCD中，AB//CD，且.‎ ‎（1）证明：平面PAB⊥平面PAD；‎ ‎（2）若PA=PD=AB=DC，，求二面角A-PB-C的余弦值.‎ ‎2、（2017新课标Ⅱ理）（12分）‎ 如图，四棱锥P-ABCD中，侧面PAD为等边三角形且垂直于底面ABCD， E是PD的中点．‎ ‎（1）证明：直线平面PAB；‎ ‎（2）点M在棱PC 上，且直线BM与底面ABCD所成角为，求二面角的余弦值．‎ ‎3、（2017新课标Ⅲ理数）（12分）‎ 如图，四面体ABCD中，△ABC是正三角形，△ACD是直角三角形，∠ABD=∠CBD，AB=BD．‎ ‎（1）证明：平面ACD⊥平面ABC；‎ ‎（2）过AC的平面交BD于点E，若平面AEC把四面体ABCD 分成体积相等的两部分，求二面角D–AE–C的余弦值．‎ ‎4、（2017北京理）（本小题14分）‎ 如图，在四棱锥P-ABCD中，底面ABCD为正方形，平面PAD⊥平面 ABCD，点M在线段PB上，PD//平面MAC，PA=PD=，AB=4．‎ ‎（I）求证：M为PB的中点；‎ ‎（II）求二面角B-PD-A的大小；‎ ‎（III）求直线MC与平面BDP所成角的正弦值．‎ ‎5、（2017山东理）如图，几何体是圆柱的一部分，它是由矩形（及其内部）以边所在直线为旋转轴旋转得到的，是的中点.‎ ‎（Ⅰ）设是上的一点，且，求的大小；‎ ‎（Ⅱ）当，，求二面角的大小.‎ ‎6、（2017江苏）（本小题满分14分）‎ ‎ 如图，在三棱锥A-BCD中，AB⊥AD，BC⊥BD，平面ABD⊥平面BCD，点E，F(E与A，D不重合)分别在棱AD，BD上，且EF⊥AD．‎ ‎ 求证：（1）EF∥平面ABC；‎ ‎ （2）AD⊥AC．‎ ‎7、如图，在三棱锥P-ABC中，PA⊥底面ABC，∠BAC＝90°，点D、E、N分别为棱PA、PC、BC的中点，M是线段AD的中点，PA＝AC＝4，AB＝2‎ ‎（1）求证：MN∥平面BDE；‎ ‎（2）求二面角C-EM-N的正弦值；‎ ‎（3）已知点H在棱PA上，且直线NH与直线BE所成角的余弦值为，求线段AH的长。‎ ‎8、（2017浙江）（本题满分15分）如图，已知四棱锥P–ABCD，△PAD是以AD 为斜边的等腰直角三角形，，CD⊥AD，PC=AD=2DC=2CB，E为PD的中点．‎ ‎（第19题图）‎ ‎（Ⅰ）证明：平面PAB；‎ ‎（Ⅱ）求直线CE与平面PBC所成角的正弦值．‎