江苏省淮安市六所四星级中学2019-2020学年高一下学期联考数学试题 Word版含解析 20页

www.ks5u.com 淮安地区六校联考试题 一、单项选择题 ‎1.已知直线经过两点，则的斜率为（）‎ A. B. C. D. ‎ ‎【答案】A ‎【解析】‎ ‎【分析】‎ 直接代入两点的斜率公式，计算即可得出答案．‎ ‎【详解】 ‎ 故选A ‎【点睛】本题考查两点的斜率公式，属于基础题．‎ ‎2.在中，，，则外接圆的半径为（ ）‎ A. B. C. 2 D. 4‎ ‎【答案】C ‎【解析】‎ ‎【分析】‎ 直接根据正弦定理求解即可．‎ ‎【详解】解：∵，，‎ ‎∴外接圆半径，‎ 故选：C．‎ ‎【点睛】本题主要考查正弦定理的应用，属于基础题．‎ ‎3.下列命题中是真命题的是（ ）‎ A. 垂直于同一条直线的两条直线互相平行 B. 与同一个平面夹角相等的两条直线互相平行 C. 平行于同一个平面的两条直线互相平行 D. 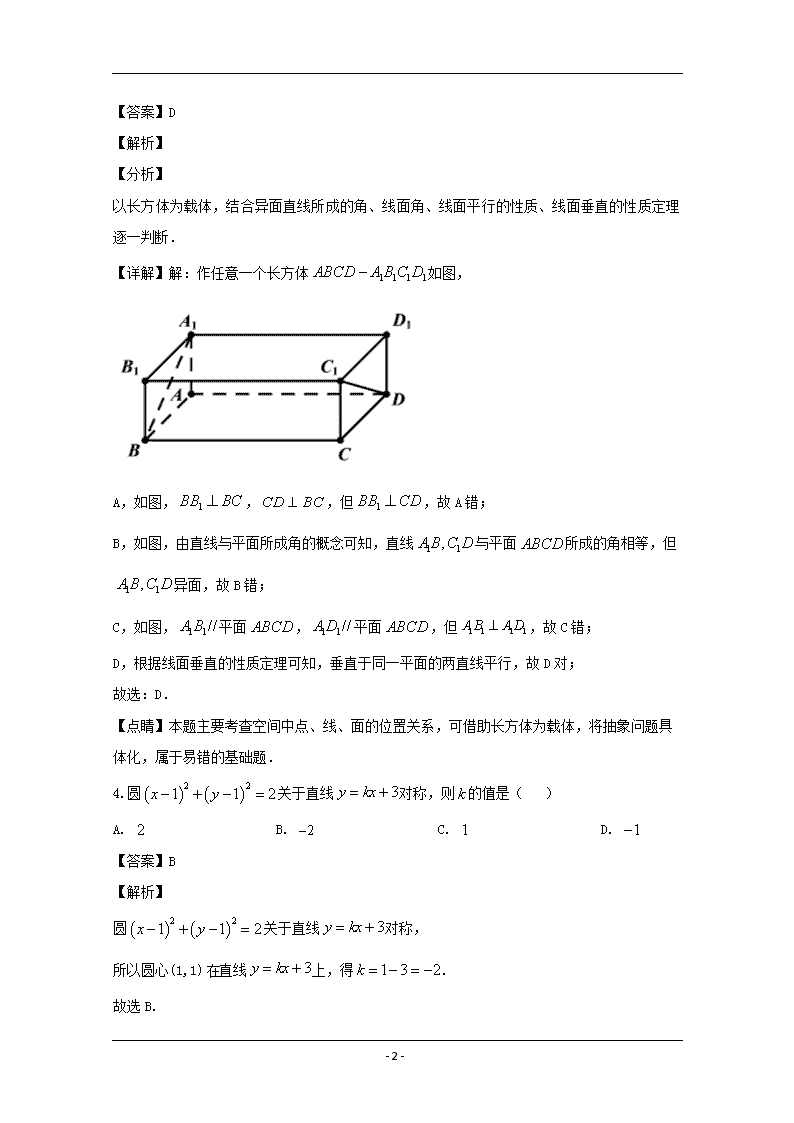垂直于同一平面两直线平行 - 20 -‎ ‎【答案】D ‎【解析】‎ ‎【分析】‎ 以长方体为载体，结合异面直线所成的角、线面角、线面平行的性质、线面垂直的性质定理逐一判断．‎ ‎【详解】解：作任意一个长方体如图，‎ A，如图，，，但，故A错；‎ B，如图，由直线与平面所成角的概念可知，直线与平面所成的角相等，但异面，故B错；‎ C，如图，平面，平面，但，故C错；‎ D，根据线面垂直的性质定理可知，垂直于同一平面的两直线平行，故D对；‎ 故选：D．‎ ‎【点睛】本题主要考查空间中点、线、面的位置关系，可借助长方体为载体，将抽象问题具体化，属于易错的基础题．‎ ‎4.圆关于直线对称，则的值是（ ）‎ A. B. C. D. 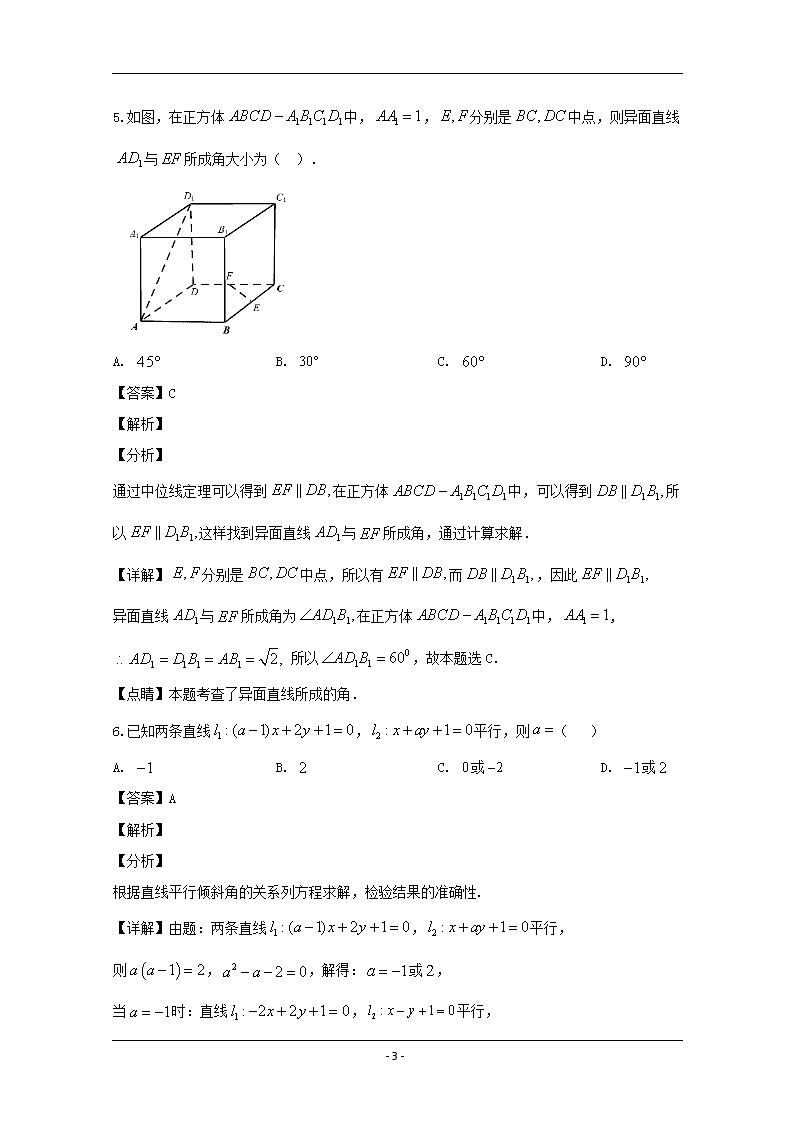‎ ‎【答案】B ‎【解析】‎ 圆关于直线对称，‎ 所以圆心(1,1)直线上，得.‎ 故选B.‎ - 20 -‎ ‎5.如图，在正方体中，，分别是中点，则异面直线与所成角大小为（ ）．‎ A. B. C. D. ‎ ‎【答案】C ‎【解析】‎ ‎【分析】‎ 通过中位线定理可以得到在正方体中，可以得到所以这样找到异面直线与所成角，通过计算求解．‎ ‎【详解】分别是中点，所以有而，因此 异面直线与所成角为在正方体中，,‎ ‎ 所以，故本题选C．‎ ‎【点睛】本题考查了异面直线所成的角．‎ ‎6.已知两条直线，平行，则（ ）‎ A. B. C. 或 D. 或 ‎【答案】A ‎【解析】‎ ‎【分析】‎ 根据直线平行倾斜角的关系列方程求解，检验结果的准确性.‎ ‎【详解】由题：两条直线，平行，‎ 则，，解得：或，‎ 当时：直线，平行，‎ - 20 -‎ 当时：直线，重合，（舍去），‎ 所以.‎ 故选：A ‎【点睛】此题考查根据两条直线平行求参数范围，注意考虑直线重合的情况，容易产生增根.‎ ‎7.记的三内角的对边边长分别为，若则( )‎ A. B. C. D. ‎ ‎【答案】D ‎【解析】‎ ‎【分析】‎ 由，可得，利用二倍角公式，进行化简，通过正弦定理实现角边转化，根据已知，即可求出的值．‎ ‎【详解】由 （1）,由正弦定理可知：‎ ‎,代入（1）中 ，可得，又 ，故本题选D．‎ ‎【点睛】本题考查了正弦定理、二倍角的正弦公式．‎ ‎8.设，过定点的动直线和过定点的动直线交于点，则的值为（ ）‎ A. 5 B. 10 C. D. ‎ ‎【答案】B ‎【解析】‎ ‎【分析】‎ 由题意先求出定点的定点的坐标，再求出交点，再根据两点间距离公式即可求出答案．‎ ‎【详解】解：由题意，动直线经过定点，则，‎ - 20 -‎ 动直线变形得，则，‎ 由得，‎ ‎∴‎ ‎，‎ 故选：B．‎ ‎【点睛】本题主要考查直线过定点问题，考查两点间距离公式及两条直线的交点问题，考查计算能力，属于基础题．‎ 二、多项选择题 ‎9.已知直线过点（1，2），且在横坐标与纵坐标上的截距的绝对值相等的直线方程可以是下列（ ）选项.‎ A. 2x-y=0 B. x+y=3 C. x-2y=0 D. x-y+1=0‎ ‎【答案】ABD ‎【解析】‎ ‎【分析】‎ 由题意设所求直线的横截距为，分和两种情况讨论，结合直线的截距式方程即可求出答案．‎ ‎【详解】解：由题意设所求直线的横截距为，‎ ‎（1）当时，由题意可设直线的方程为，将代入可得，‎ ‎∴直线的方程为；‎ ‎（2）当时，由截距式方程可得直线的方程为（截距相等）或 - 20 -‎ ‎（截距相反），将代入可得或，‎ ‎∴直线的方程为或；‎ 故选：ABD．‎ ‎【点睛】本题主要考查直线的截距的应用，考查直线的截距式方程，考查分类讨论思想，属于基础题．‎ ‎10.如图所示，PA垂直于以AB为直径的圆O所在的平面，C为圆上异于A，B的任一点，则下列关系中正确的是（ ）‎ A. PA⊥BC B. AC⊥PB C. BC⊥平面PAC D. PC⊥PB ‎【答案】AC ‎【解析】‎ ‎【分析】‎ 由题意，平面，则由线面垂直的性质可得A对；而，则由线面垂直的判定定理可得平面，即C对；B采用反证法排除；由平面可得，故D错．‎ ‎【详解】解：由题意有，平面，‎ ‎∵平面，‎ ‎∴，故A对；‎ 而，且，平面，‎ ‎∴平面，故C对；‎ 若，因为，可得平面，则，与题目矛盾，故B错；‎ 由平面可得，，则为直角三角形，‎ 若，则重合，与已知矛盾，故D错；‎ - 20 -‎ 故选：AC．‎ ‎【点睛】本题主要考查线面垂直的判定与性质，属于基础题．‎ ‎11.在中，，则的面积可以是（ ）‎ A. B. 1 C. D. ‎ ‎【答案】AD ‎【解析】‎ ‎【分析】‎ 由余弦定理求出，再根据三角形的面积公式即可求出答案．‎ ‎【详解】解：∵，‎ 由余弦定理得，‎ ‎∴，‎ ‎∴，或，‎ ‎∴由的面积公式得或，‎ 故选：AD．‎ ‎【点睛】本题主要考查三角形的面积公式的应用，考查余弦定理解三角形，属于基础题．‎ ‎12.已知圆方程为：与直线x+my-m-2=0，下列选项正确的是（ ）‎ A. 直线与圆必相交 B. 直线与圆不一定相交 C. 直线与圆相交且所截最短弦长为 D. 直线与圆可以相切 ‎【答案】AC ‎【解析】‎ ‎【分析】‎ 求出直线经过的定点，根据定点与圆的位置关系即可判断直线与圆的位置关系，结合几何知识可知当直线与过定点和圆心的直线垂直时，弦长有最小值，由此可求出答案．‎ ‎【详解】解：由题意，圆的圆心，半径，‎ 直线变形得，得直线过定点，‎ - 20 -‎ ‎∵，‎ ‎∴直线与圆必相交，故A对，B、D错；‎ 由平面几何知识可知，当直线与过定点和圆心的直线垂直时，弦长有最小值，‎ 此时弦长为，故C对；‎ 故选：AC．‎ ‎【点睛】本题主要考查直线与圆的位置关系，考查数形结合思想，属于基础题．‎ 三、填空题 ‎13.过直线与的交点，且垂直于直线的直线方程是_______．‎ ‎【答案】‎ ‎【解析】‎ ‎【分析】‎ 先求交点，再根据垂直关系得直线方程.‎ ‎【详解】直线与的交点为,‎ 垂直于直线的直线方程可设为,‎ 所以,即.‎ ‎【点睛】本题考查两直线垂直与交点，考查基本分析求解能力，属基础题.‎ ‎14.平面相交，在内取两点A，B，在内取两点C，D，这四点都不在交线上，则直线AB与直线CD的位置关系为_______.‎ ‎【答案】相交或平行或异面 ‎【解析】‎ ‎【分析】‎ - 20 -‎ 作图，设设，结合图象分类讨论与、与的关系，由此可得答案．‎ ‎【详解】解：如图，设，‎ 当，时，；‎ 当与相交、与相交时，‎ 若交点相同，则直线与相交；若交点不同，则直线与异面；‎ 故答案为：相交或平行或异面．‎ ‎【点睛】本题主要考查空间中的两条直线的位置关系，考查数形结合思想，考查空间想象能力，属于基础题．‎ ‎15.中，，则的面积为_________；边上中线的长为_____________.‎ ‎【答案】 (1). (2). ‎ ‎【解析】‎ ‎【分析】‎ 由得，根据三角形的面积公式可得第一空答案；由余弦定理可求得，再用余弦定理可求得，再用余弦定理即可求得第二空答案．‎ ‎【详解】解：∵，，‎ ‎∴，‎ ‎∵，‎ ‎∴的面积为；‎ - 20 -‎ 由余弦定理得，‎ ‎∴，则，‎ 由余弦定理得，‎ ‎∴，解得，‎ 故答案为：；．‎ ‎【点睛】本题主要考查余弦定理解三角形，考查三角形的面积公式，属于基础题．‎ ‎16.在平面直角坐标中，已知点，若直线上存在点使得，则实数的取值范围是_______．‎ ‎【答案】‎ ‎【解析】‎ ‎【分析】‎ 根据得出点的轨迹方程，又点在直线上，则点的轨迹与直线必须有公共点，进而解决问题.‎ ‎【详解】解：设 则，‎ 因为，‎ 所以有，‎ 同时平方，化简得，‎ 故点的轨迹为圆心在（0,0），半径2为的圆，‎ - 20 -‎ 又点在直线上，‎ 故圆与直线必须有公共点，‎ 所以，解得.‎ ‎【点睛】本题考查了点的轨迹问题、直线与圆的位置关系的问题，解题的关键是能从题意中转化出动点的轨迹，并能求出点的轨迹方程.‎ 四、解答题 ‎17.如图，长方体中，，，‎ ‎（1）求异面直线和所成的角；‎ ‎（2）求证：直线平面.‎ ‎【答案】（1）；（2）证明见解析．‎ ‎【解析】‎ ‎【分析】‎ ‎（1）由可得为异面直线和所成的角，解直角三角形即可求出答案；‎ ‎（2）连接，则，根据线面平行的判定定理即可证明．‎ ‎【详解】（1）解：由题意，，‎ ‎∴为异面直线和所成的角，‎ ‎∵，，‎ ‎∴，‎ ‎∴，‎ - 20 -‎ 即异面直线和所成的角为；‎ ‎（2）证：连接，‎ ‎∵，且，‎ ‎∴四边形为平行四边形，‎ ‎∴，‎ 又平面，平面，‎ ‎∴直线平面．‎ ‎【点睛】本题主要考查线面平行的证明，考查异面直线所成的角的求法，属于基础题．‎ ‎18.已知直线（不同时为0）, .‎ ‎⑴若且，求实数a值；‎ ‎(2)当且时，求直线与之间的距离.‎ ‎【答案】（1）2；（2）‎ ‎【解析】‎ ‎【分析】‎ ‎（1）当b=0时，l1垂直于x轴，所以由l1⊥l2知l2垂直于y轴，由此能求出实数a的值；‎ ‎（2）由b=3且l1∥l2，先求出a值，再由两条平行间的距离公式，能求出直线l1与l2之间的距离．‎ ‎【详解】（1）当b=0，时，l1：ax+1=0，‎ 由l1⊥l2知a﹣2=0， ‎ 解得a=2．‎ ‎（2）当b=3时，l1：ax+3y+1=0，‎ - 20 -‎ 当l1∥l2时，有 解得a=3，‎ 此时，l1的方程为：3x+3y+1=0，‎ l2的方程为：x+y+3=0，‎ 即3x+3y+9=0，‎ 则它们之间的距离为d==．‎ ‎【点睛】本题考查两条直线平行和两条直线垂直的条件的应用，解题时要认真审题，注意两条平行线间的距离公式的灵活运用．‎ ‎19.在中，已知．‎ ‎（1）求角的大小；‎ ‎（2）求的值．‎ ‎【答案】(1) (2) ‎ ‎【解析】‎ ‎【分析】‎ ‎（1）直接使用余弦定理即可得解；‎ ‎（2）法1：由（1）可以求出，由三角形内角和定理，可以求出的关系，用正弦定理，求出,进而求出，也就求出，，最后求出的值；‎ 法2：直接利用余弦定理得，，再利用同角的三角函数关系，求出，最后利用二角差的余弦公式求出的值．‎ ‎【详解】解：(1)由余弦定理得：，‎ 因为，所以． ‎ ‎(2)法1 由正弦定理得：，‎ - 20 -‎ 所以．‎ 又因为，所以 即，所以 所以，．‎ 因为．所以，所以，‎ 所以 ‎ 法2 直接利用余弦定理得，‎ 求得，所以 ‎【点睛】本题考查了正弦定理、余弦定理．‎ ‎20.如图，在四棱锥中，底面是正方形，侧棱底面，，是的中点.‎ ‎（1）证明平面;‎ ‎（2）证明:平面.‎ - 20 -‎ ‎【答案】(1)见详解；（2）见详解.‎ ‎【解析】‎ ‎【分析】‎ ‎（1）根据线面平行的判定定理，可得平面;‎ ‎（2）根据线面垂直的判定定理可判定平面.‎ ‎【详解】(1)记中点为，连，由分别为中点，‎ 所以 又平面 ，平面， ‎ 所以平面；‎ ‎(2) 由底面，‎ 所以，‎ 又 ，，‎ 所以平面，‎ 所以，‎ 由， 为中点，‎ 所以 又，‎ 所以平面.‎ ‎【点睛】本题主要考查线面平行和线面垂直，熟记判定定理即可，属于基础题型.‎ ‎21.如图，某公园内有两条道路AB， AP， 现计划在AP上选择一点C，新建道路BC，并把△ABC - 20 -‎ 所在区域改造成绿化区域，已知∠BAC=，AB=2km.‎ ‎（1） 若绿化区域△ABC的面积为，求道路BC的长度；‎ ‎（2） 绿化区域△ABC每的改造费用与新建道路BC每km修建费用都是角∠ACB的函数，其中绿化区域△ABC改造费用为万元/，新建道路BC新建费用为万元/ km，设，某工程队承包了该公园的绿化区域改造与新道路修建，已知绿化区域改造费与道路新建费用越高，则工程队所获利润也越高，试问当为何值时，该工程队获得最高利润?‎ ‎【答案】（1）；（2）当时，该工程队获得最高利润．‎ ‎【解析】‎ ‎【分析】‎ ‎（1）根据三角形面积公式求出，再根据余弦定理求出；‎ ‎（2）设绿化区域改造费与道路新建费用之和为万元，由题意得，由正弦定理可求得，，根据题意结合三角恒等变换公式以及辅助角公式可得，再结合三角函数的性质即可求得答案．‎ ‎【详解】解：（1）∵绿化区域的面积为，‎ ‎∴，‎ ‎∵，，‎ ‎∴，得，‎ 由余弦定理得 - 20 -‎ ‎，‎ ‎∴，‎ 即的长度为；‎ ‎（2）设绿化区域改造费与道路新建费用之和为万元，‎ ‎∵，，‎ ‎∴，‎ 由正弦定理得，‎ ‎，，‎ 则由题意可得 ‎，‎ ‎∵，‎ ‎∴，‎ ‎∴，当且仅当即时取等号，‎ - 20 -‎ ‎∴当时，该工程队获得最高利润．‎ ‎【点睛】本题主要考查正弦定理和余弦定理的应用，考查三角形的面积公式的应用，考查简单的三角恒等变换，考查计算能力，属于中档题．‎ ‎22.已知圆，直线 ‎（1）若直线与圆O交于不同的两点A， B，当时，求k的值.‎ ‎（2）若k=1，P是直线上的动点，过P作圆O的两条切线PC、PD，切点为C、D，问：直线CD是否过定点?若过定点，求出定点坐标；若不过定点，说明理由.‎ ‎（3）若EF、GH为圆的两条相互垂直的弦，垂足为M(1，)，求四边形EGFH的面积的最大值 ‎【答案】（1）；（2）直线过定点；（3）5．‎ ‎【解析】‎ ‎【分析】‎ ‎（1）当时，为等腰直角三角形，求出点到的距离，然后求解即可；‎ ‎（2）设，由题意可知：、、、四点共圆且在以为直径的圆上，该圆的方程为，利用、在圆上，求出公共弦所在直线的方程，利用直线系求解即可；‎ ‎（3）设圆心到直线、的距离分别为，，通过，求出面积表达式，然后求解最值．‎ ‎【详解】解：（1）由题意，圆的圆心为，半径，‎ 有根据题意，当时，为等腰直角三角形，‎ ‎∴圆心到直线的距离，‎ ‎∴；‎ ‎（2）由题意，直线，‎ - 20 -‎ 设，由题意可知、、、四点共圆且在以为直径的圆上，‎ 其方程为，即，‎ 又、在圆上，‎ 由公共弦所在直线方程的求法可得，‎ 直线的方程为，即，‎ 由得，‎ 直线过定点；‎ ‎（3）设圆心到直线、的距离分别为，，‎ 则，‎ ‎，，‎ ‎，‎ 当且仅当即时，等号成立，‎ 四边形的面积的最大值为5．‎ ‎【点睛】本题主要考查直线与圆的方程的综合应用，直线系方程的应用，考查转化与划归思想，考查计算能力，属于中档题．‎ ‎ ‎ - 20 -‎ - 20 -‎