- 1.16 MB
- 2021-05-26 发布
第六章 平行四边形
6.2 平行四边形的判定(1)
A D
B C
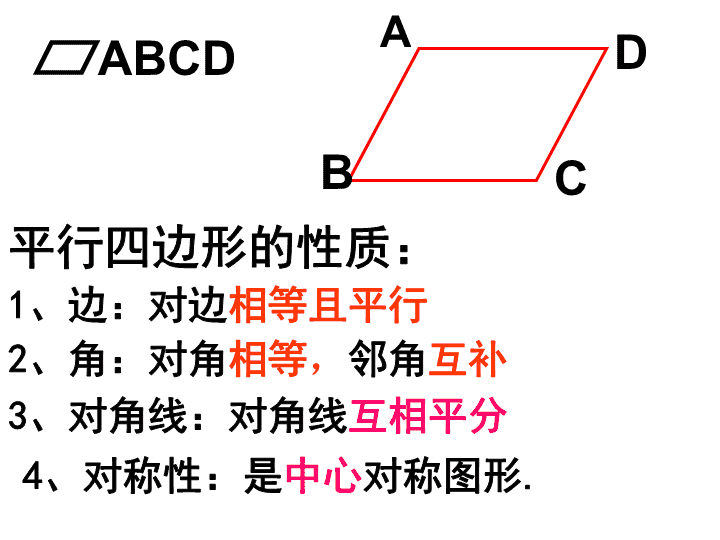
ABCD
平行四边形的性质:
1、边:对边相等且平行
2、角:对角相等,邻角互补
4、对称性:是中心对称图形.
3、对角线:对角线互相平分
平行四边形的判定:
有关边的判定是3个:
1、两组对边分别平行的四边形是
平行四边形
用几何语言表示:
∵AB∥CD,AD∥BC
∴四边形ABCD是平行四边形
平行四边形的判定:
有关边的判定是3个:
2、两组对边分别相等的四边形是
平行四边形
已知:如图,在四边形ABCD中,
AB=CD,BC=AD.求证:四边
形ABCD是平行四边形.
1
2
3
4
证明:连接BD.
在△ABD和△CDB中
∵ AB=CD AD=CB BD=DB
∴ △ABD≌△CDB
∴ ∠1=∠2 ∠3=∠4
∴ AB∥CD AD∥CB
∴ 四边形ABCD是平行四边形
平行四边形的判定:
有关边的判定是3个:
2、两组对边分别相等的四边形是
平行四边形
用几何语言表示:
∵AB=CD,AD=BC
∴四边形ABCD是平行四边形
平行四边形的判定:
有关边的判定是3个:
3、一组对边平行且相等的四边
形是平行四边形
如图,在四边形ABCD中,
AB∥CD, 且AB=CD.
求证:四边形ABCD是平行四边
形.
21
证明:连接AC.
∵ AB∥CD
∴ ∠1=∠2
又∵ AB=CD AC=CA
∴ △BAC≌ △DCA
∴ BC=AD
∴ 四边形ABCD是平行四边形
平行四边形的判定:
有关边的判定是3个:
3、一组对边平行且相等的四边
形是平行四边形
用几何语言表示:
∵AB=CD, AB∥CD,
∴四边形ABCD是平行四边形
AD=CB,
AD∥CB,
平行四边形的判定:
有关边的判定是3个:
1、两组对边分别平行的四边形是
平行四边形
3、一组对边平行且相等的四边
形是平行四边形
2、两组对边分别相等的四边形是
平行四边形
例1 如图,在平行四边形ABCD
中,E、F分别是AD和BC的中
点.求证:四边形BFDE是平行
四边形.
证明:∵ 四边形ABCD是平行四边
形∴ AD=CB AD//BC
∵E、F分别是AD和BC的中点
∴ ED=1/2AD BF=1/2BC∴ DE=BF
∵ED∥BF
∴ 四边形BFDE是平行四边形
如图:线段AD是线段BC经过平移所
得到的,分别连接AB、CD.四边形
ABCD是平行四边形吗?为什么?
巩固练习
(1)判定一个四边形是平行四边形的方法
有哪几种?这些方法是从什么角度去考虑的?
(2)我们是通过什么方法得出平行四边形的
这几种判定方法的,这样的探索过程对你有
什么启发?
课堂小结
相关文档
- 八年级下数学课件《函数的表示》课2021-05-26 02:50:2821页
- 八年级下数学课件《分式的基本性质2021-05-26 02:34:5316页
- 八年级下数学课件八年级下册数学课2021-05-26 02:03:3917页
- 八年级下数学课件《抽样调查》课件2021-05-26 00:24:0416页
- 八年级下数学课件20-2《函数》ppt2021-05-26 00:02:3518页
- 八年级下数学课件《矩形、菱形、正2021-05-25 23:41:3126页
- 八年级下数学课件21-2《一次函数的2021-05-25 23:38:5215页
- 八年级下数学课件《中心对称与轴对2021-05-25 23:19:2419页
- 八年级下数学课件八年级下册数学课2021-05-25 22:28:3912页
- 八年级下数学课件《分式方程》 (7)2021-05-25 22:01:0216页