浙江省2021届高考数学一轮复习第五章三角函数解三角形第6节三角函数的图象与性质课件 44页

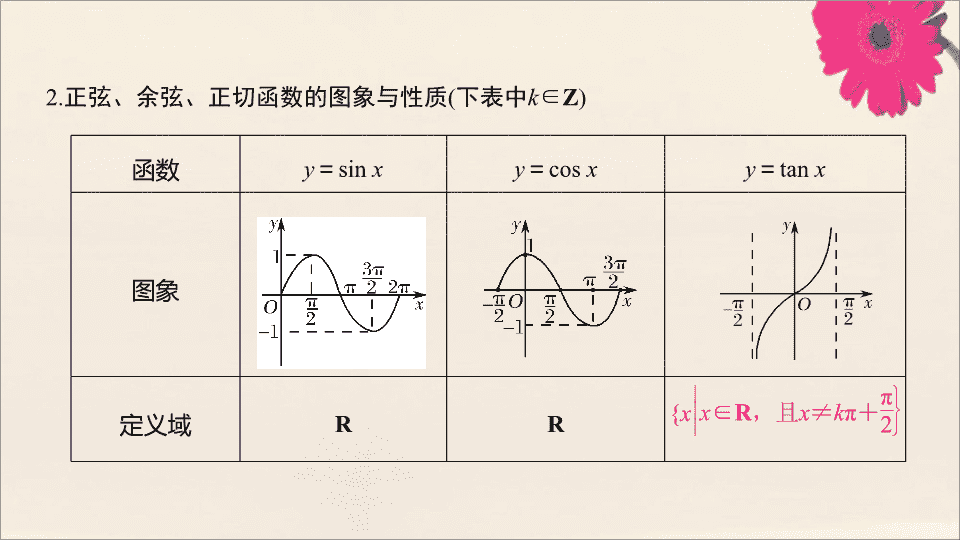
第 6 节　三角函数的图象与性质 知 识 梳 理 (π ，－ 1) 2 . 正弦、余弦、正切函数的图象与性质 ( 下表中 k ∈ Z ) 函数 y ＝ sin x y ＝ cos x y ＝ tan x 图象 定义域 R R 值域 R 周期性 2π 奇偶性 奇函数 递增区间 递减区间 无 [2 k π ， 2 k π ＋ π] [ － 1 ， 1] [ － 1 ， 1] 2π π 奇函数 偶函数 [2 k π － π ， 2 k π] ( k π ， 0) x ＝ k π 诊 断 自 测 1. 判断下列说法的正误 . 解析　 (1) 函数 y ＝ sin x 的周期是 2 k π( k ∈ Z ). (2) 余弦函数 y ＝ cos x 的对称轴有无穷多条， y 轴只是其中的一条 . (4) 当 k >0 时， y max ＝ k ＋ 1 ；当 k <0 时， y max ＝－ k ＋ 1. 答案 　 (1) × 　 (2) × 　 (3) × 　 (4) × 　 (5) √ 答案　 D 3. (2018· 全国 Ⅰ 卷 ) 已知函数 f ( x ) ＝ 2cos 2 x － sin 2 x ＋ 2 ，则 ( 　　 ) A. f ( x ) 的最小正周期为 π ，最大值为 3 B. f ( x ) 的最小正周期为π，最大值为 4 C. f ( x ) 的最小正周期为 2π ，最大值为 3 D. f ( x ) 的最小正周期为 2π ，最大值为 4 答案　 B 答案　 C 考点一　三角函数的定义域及三角不等式 规律方法 　 (1) 三角函数定义域的求法 ① 以正切函数为例，应用正切函数 y ＝ tan x 的定义域求函数 y ＝ A tan( ωx ＋ φ ) 的定义域 . ② 转化为求解简单的三角不等式求复杂函数的定义域 . (2) 简单三角不等式的解法 ① 利用三角函数线求解 . ② 利用三角函数的图象求解 . (2) 法一 　要使函数有意义，必须使 sin x － cos x ≥ 0. 利用图象，在同一坐标系中画出 [0 ， 2π] 上 y ＝ sin x 和 y ＝ cos x 的图象，如图所示 . 法二　 利用三角函数线，画出满足条件的终边范围 ( 如图阴影部分所示 ). 考点二　三角函数的值域 规律方法 　 求解三角函数的值域 ( 最值 ) 常见到以下几种类型 ： (1) 形如 y ＝ a sin x ＋ b cos x ＋ c 的三角函数化为 y ＝ A sin( ωx ＋ φ ) ＋ c 的形式，再求值域 ( 最值 ) ； (2) 形如 y ＝ a sin 2 x ＋ b sin x ＋ c 的三角函数，可先设 sin x ＝ t ，化为关于 t 的二次函数求值域 ( 最值 ) ； (3) 形如 y ＝ a sin x cos x ＋ b (sin x ±cos x ) ＋ c 的三角函数，可先设 t ＝ sin x ±cos x ，化为关于 t 的二次函数求值域 ( 最值 ). ＝－ cos 2 x － 3cos x ＝－ 2cos 2 x － 3cos x ＋ 1 答案　 (1)A 　 (2) － 4 　 (3)B 考点三　三角函数的性质 角度 1 　三角函数的奇偶性与周期性 多维探究 规律方法 　 (1) 求较为复杂的三角函数的单调区间时，首先化简成 y ＝ A sin( ωx ＋ φ ) 形式，再求 y ＝ A sin( ωx ＋ φ ) 的单调区间，只需把 ωx ＋ φ 看作一个整体代入 y ＝ sin x 的相应单调区间内即可，注意要先把 ω 化为正数 .(2) 对于已知函数的单调区间的某一部分确定参数 ω 的范围的问题，首先，明确已知的单调区间应为函数的单调区间的子集，其次，要确定已知函数的单调区间，从而利用它们之间的关系可求解，另外，若是选择题利用特值验证排除法求解更为简捷 .