高中数学（人教版a版选修2-1）配套课时作业：第三章 空间向量与立体几何 章末总结 word版含答案 7页

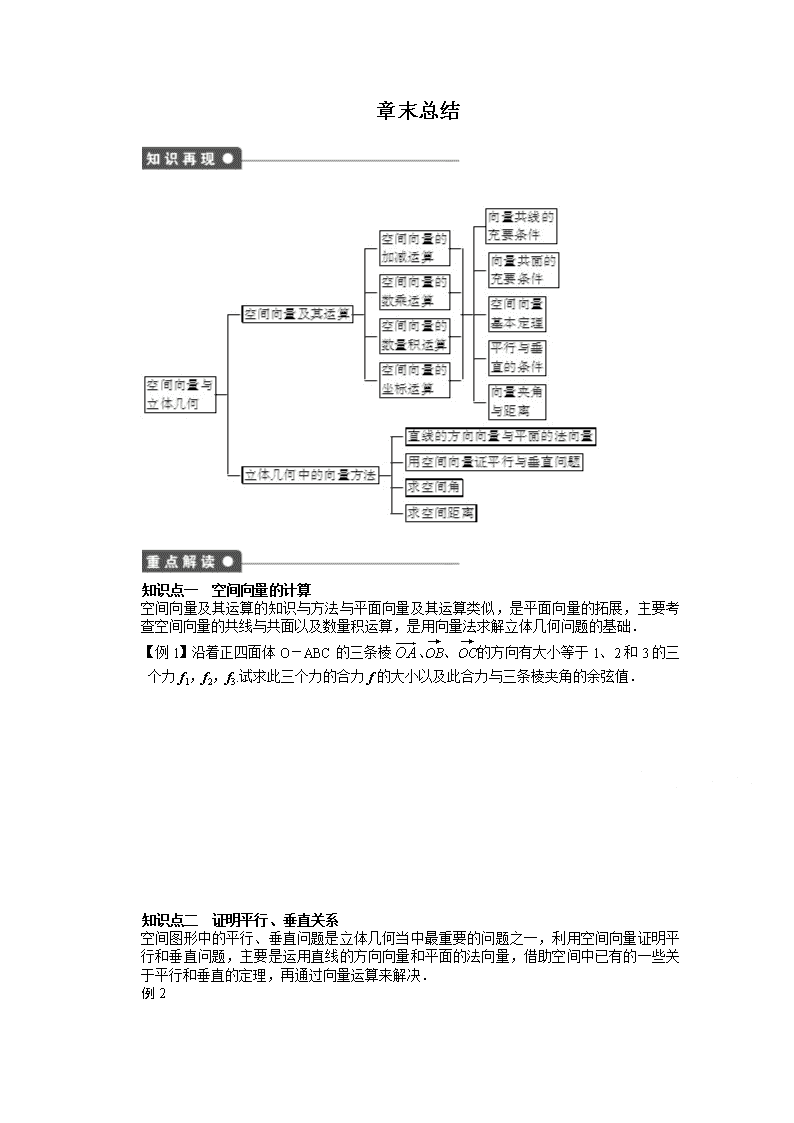
章末总结 知识点一 空间向量的计算 空间向量及其运算的知识与方法与平面向量及其运算类似，是平面向量的拓展，主要考 查空间向量的共线与共面以及数量积运算，是用向量法求解立体几何问题的基础． 【例 1】沿着正四面体 O－ABC 的三条棱OA  、OB→ 、OC→ 的方向有大小等于 1、2 和 3 的三 个力 f1，f2，f3.试求此三个力的合力 f 的大小以及此合力与三条棱夹角的余弦值． 知识点二 证明平行、垂直关系 空间图形中的平行、垂直问题是立体几何当中最重要的问题之一，利用空间向量证明平 行和垂直问题，主要是运用直线的方向向量和平面的法向量，借助空间中已有的一些关 于平行和垂直的定理，再通过向量运算来解决． 例 2 如图，正方体 ABCD—A1B1C1D1 中，M、N 分别为 AB、B1C 的中点． (1)用向量法证明平面 A1BD∥平面 B1CD1； (2)用向量法证明 MN⊥面 A1BD. 例 3 如图，在棱长为 1 的正方体 ABCD—A1B1C1D1 中，P 是侧棱 CC1 上的一点，CP＝m. 试确定 m 使得直线 AP 与平面 BDD1B1 所成的角为 60°. 例 4 正方体 ABCD—A1B1C1D1 中，E、F 分别是 BB1、CD 的中点，求证：平面 AED⊥平 面 A1FD1. 知识点三 空间向量与空间角 求异面直线所成的角、直线与平面所成的角、二面角，一般有两种方法：即几何法和向 量法，几何法求角时，需要先作出(或证出)所求空间角的平面角，费时费力，难度很大．而 利用向量法，只需求出直线的方向向量与平面的法向量．即可求解，体现了向量法极大 的优越性． 例 5 如图所示，在长方体 ABCD—A1B1C1D1 中，AB＝5，AD＝8，AA1＝4，M 为 B1C1 上一点且 B1M＝2，点 N 在线段 A1D 上，A1D⊥AN. (1)cos〈 1A D  ，AM→ 〉； (2)求直线 AD 与平面 ANM 所成角的余弦值； (3)求平面 ANM 与平面 ABCD 所成角的余弦值． 知识点四 空间向量与空间距离 近年来，对距离的考查主要体现在两点间的距离和点到平面的距离，两点间的距离可以 直接代入向量模的公式求解，点面距可以借助直线的方向向量与平面的法向量求解，或 者利用等积求高的方法求解． 例 6 如图，PA⊥平面 ABCD，四边形 ABCD 是正方形，PA＝AD＝2，M、N 分别是 AB、PC 的 中点． (1)求二面角 P—CD—B 的大小； (2)求证：平面 MND⊥平面 PCD； (3)求点 P 到平面 MND 的距离． 章末总结 重点解读 例 1 解 如图所示，用 a，b，c 分别代表棱OA→、OB→、OC→上的三个单位向量， 则 f1＝a，f2＝2b，f3＝3c， 则 f＝f1＋f2＋f3 ＝a＋2b＋3c， ∴|f|2＝(a＋2b＋3c)(a＋2b＋3c) ＝|a|2＋4|b|2＋9|c|2＋4a·b＋6a·c＋12b·c ＝14＋4cos 60°＋6cos 60°＋12 cos 60° ＝14＋2＋3＋6＝25， ∴|f|＝5，即所求合力的大小为 5. 且 cos〈f，a〉＝ f·a |f|·|a| ＝|a|2＋2a·b＋3a·c 5 ＝ 1＋1＋3 2 5 ＝ 7 10 ， 同理可得：cos〈f，b〉＝4 5 ，cos〈f，c〉＝ 9 10. 例 2 证明 (1)在正方体 ABCD—A1B1C1D1 中， BD→＝AD→－AB→，B1D1 → ＝A1D1 → －A1B1 → ， 又∵AD→＝A1D1 → ，AB→＝A1B1 → ， ∴BD→＝B1D1 → .∴BD∥B1D1. 同理可证 A1B∥D1C， 又 BD∩A1B＝B，B1D1∩D1C＝D1， 所以平面 A1BD∥平面 B1CD1. (2) MN→＝MB→＋BC→＋CN→ ＝1 2 AB→＋AD→＋1 2(CB→＋CC1 →) ＝1 2 AB→＋AD→＋1 2(－AD→＋AA1 →) ＝1 2 AB→＋1 2 AD→＋1 2 AA1 →. 设AB→＝a，AD→＝b，AA1 →＝c， 则MN→＝1 2(a＋b＋c)． 又BD→＝AD→－AB→＝b－a， ∴MN→·BD→＝1 2(a＋b＋c)(b－a) ＝1 2(b2－a2＋c·b－c·a)． 又∵A1A⊥AD，A1A⊥AB， ∴c·b＝0，c·a＝0. 又|b|＝|a|，∴b2＝a2，∴b2－a2＝0. ∴MN→·BD→＝0，∴MN⊥BD. 同理可证，MN⊥A1B，又 A1B∩BD＝B， ∴MN⊥平面 A1BD. 例 3 解 建立如图所示的空间直角坐标系， 则 A(1,0,0)，B(1,1,0)，P(0,1，m)，C(0,1,0)， D(0,0,0)， B1(1,1,1)，D1(0,0,1)． 则BD→＝(－1，－1,0)， BB1 →＝(0,0,1)， AP→＝(－1,1，m)， AC→＝(－1,1,0)． 又由AC→·BD→＝0，AC→·BB1 →＝0 知，AC→为平面 BB1D1D 的一个法向量． 设 AP 与平面 BB1D1D 所成的角为θ， 则 sin θ＝|cos〈AP→，AC→〉|＝ ＝ 2 2＋m2· 2 . 依题意得 2 2＋2m2· 2 ＝sin 60°＝ 3 2 ， 解得 m＝ 3 3 . 故当 m＝ 3 3 时，直线 AP 与平面 BDD1B1 所成角为 60°. 例 4 证明 如图，建立空间直角坐标系 Dxyz. 设正方体棱长为 1， 则 E 1，1，1 2 、D1(0,0,1)、 F 0，1 2 ，0 、A(1,0,0)． ∴DA→＝(1,0,0)＝D1A1 → ，DE→＝ 1，1，1 2 ， D1F→＝ 0，1 2 ，－1 . 设 m＝(x1，y1，z1)，n＝(x2，y2，z2)分别是平面 AED 和 A1FD1 的一个法向量． ⇒ x1＝0 x1＋y1＋1 2z1＝0 . 令 y1＝1，得 m＝(0,1，－2)． 又由 ⇒ x2＝0 1 2y2－z2＝0 ， 令 z2＝1，得 n＝(0,2,1)． ∵m·n＝(0,1，－2)·(0,2,1)＝0， ∴m⊥n，故平面 AED⊥平面 A1FD1. 例 5 解 (1)建立空间直角坐标系(如图)．则 A(0,0,0)，A1(0,0,4)，D(0,8,0)，M(5,2,4)． ∴AM→＝(5,2,4)， A1D→＝(0,8，－4)． ∴AM→·A1D→＝0＋16－16＝0， ∴AM→⊥A1D→. ∴cos〈A1D→，AM→〉＝0. (2)∵A1D⊥AM，A1D⊥AN，且 AM∩AN＝A， ∴A1D→⊥平面 ANM， ∴A1D→＝(0,8，－4)是平面 ANM 的一个法向量． 又AD→＝(0,8,0)，|A1D→|＝4 5，|AD→|＝8， A1D→·AD→＝64， ∴cos〈A1D→，AD→〉＝ 64 4 5×8 ＝ 2 5 ＝2 5 5 . ∴AD 与平面 ANM 所成角的余弦值为 5 5 . (3)∵平面 ANM 的法向量是A1D→＝(0,8，－4)， 平面 ABCD 的法向量是 a＝(0,0,1)， ∴cos〈A1D→，a〉＝－4 4 5 ＝－ 5 5 . ∴平面 ANM 与平面 ABCD 所成角的余弦值为 5 5 . 例 6 (1)解 ∵PA⊥平面 ABCD， 由 ABCD 是正方形知 AD⊥CD. ∴CD⊥面 PAD，∴PD⊥CD. ∴∠PDA 是二面角 P—CD—B 的平面角． ∵PA＝AD，∴∠PDA＝45°， 即二面角 P—CD—B 的大小为 45°. (2) 如图，建立空间直角坐标系， 则 P(0,0,2)，D(0,2,0)， C(2,2,0)，M(1,0,0)， ∵N 是 PC 的中点， ∴N(1,1,1)， ∴MN→＝(0,1,1)，ND→＝(－1,1，－1)， PD→＝(0,2，－2)． 设平面 MND 的一个法向量为 m＝(x1，y1，z1)，平面 PCD 的一个法向量为 n＝(x2，y2，z2)． ∴m·MN→＝0，m·ND→＝0， 即有 y1＋z1＝0， －x1＋y1－z1＝0. 令 z1＝1，得 x1＝－2，y1＝－1. ∴m＝(－2，－1,1)． 同理，由 n·ND→＝0，n·PD→＝0， 即有 －x2＋y2－z2＝0， 2y2－2z2＝0. 令 z2＝1，得 x2＝0，y2＝1，∴n＝(0,1,1)． ∵m·n＝－2×0＋(－1)×1＋1×1＝0， ∴m⊥n.∴平面 MND⊥平面 PCD. (3)设 P 到平面 MND 的距离为 d. 由(2)知平面 MND 的法向量 m＝(－2，－1,1)， ∵PD→·m＝(0,2，－2)·(－2，－1,1)＝－4， ∴|PD→·m|＝4， 又|m|＝ －2 2＋ －1 2＋12＝ 6， ∴d＝ ＝ 4 6 ＝2 6 3 . 即点 P 到平面 MND 的距离为2 6 3 .