- 298.50 KB
- 2021-04-14 发布
27.1.2 圆的对称性
第2课时 垂径定理
知|识|目|标
1.通过折叠、作图等方法,探索出圆是轴对称图形.
2.通过圆的对称性探索出垂径定理及其推论,会用垂径定理解决有关的证明和计算问题.
3.会利用垂径定理解决实际生活中的问题.
目标一 理解圆的轴对称性
例1 教材补充例题 下列说法正确的是( )
A.每一条直径都是圆的对称轴
B.圆的对称轴是唯一的
C.圆的对称轴一定经过圆心
D.圆的对称轴是经过圆内任意一点的直线
【归纳总结】圆的对称轴的“两点注意”:
(1)圆有无数条对称轴,任何一条直径所在的直线都是圆的对称轴.
(2)对称轴是直线而不是线段,所以说“圆的对称轴是直径所在的直线”或说成“圆的对称轴是经过圆心的每一条直线”.
目标二 能应用垂径定理及其推论进行证明或计算
例2 教材补充例题 如图27-1-9,AB是⊙O的直径,弦CD⊥AB,垂足为M,下列结论不成立的是( )
图27-1-9
A.CM=DM B.= C.∠ACD=∠ADC D.OM=MB
【归纳总结】垂径定理的“三点注意”:
(1)垂径定理中的直径可以是直径、半径或过圆心的直线(线段),其本质是“过圆心”.
(2)当垂径定理中的弦为直径时,结论仍然成立.
(3)平分两条弧是指平分这条弦所对的优弧和劣弧,不要漏掉优弧.
例3 教材补充例题 如图27-1-10,AB是⊙O的直径,CD为弦,AB⊥CD,垂足为H,连结BC,BD.
(1)求证:BC=BD;
(2)已知CD=6,OH=2,求⊙O的半径.
4
图27-1-10
【归纳总结】垂径定理中常作的两种辅助线:
(1)若已知圆心,则过圆心作垂直于弦的直径(或半径或线段).
(2)若已知弧、弦的中点,则作弧、弦中点的连线或连结圆心和弦的端点等.
目标三 会用垂径定理解决实际生活中的问题
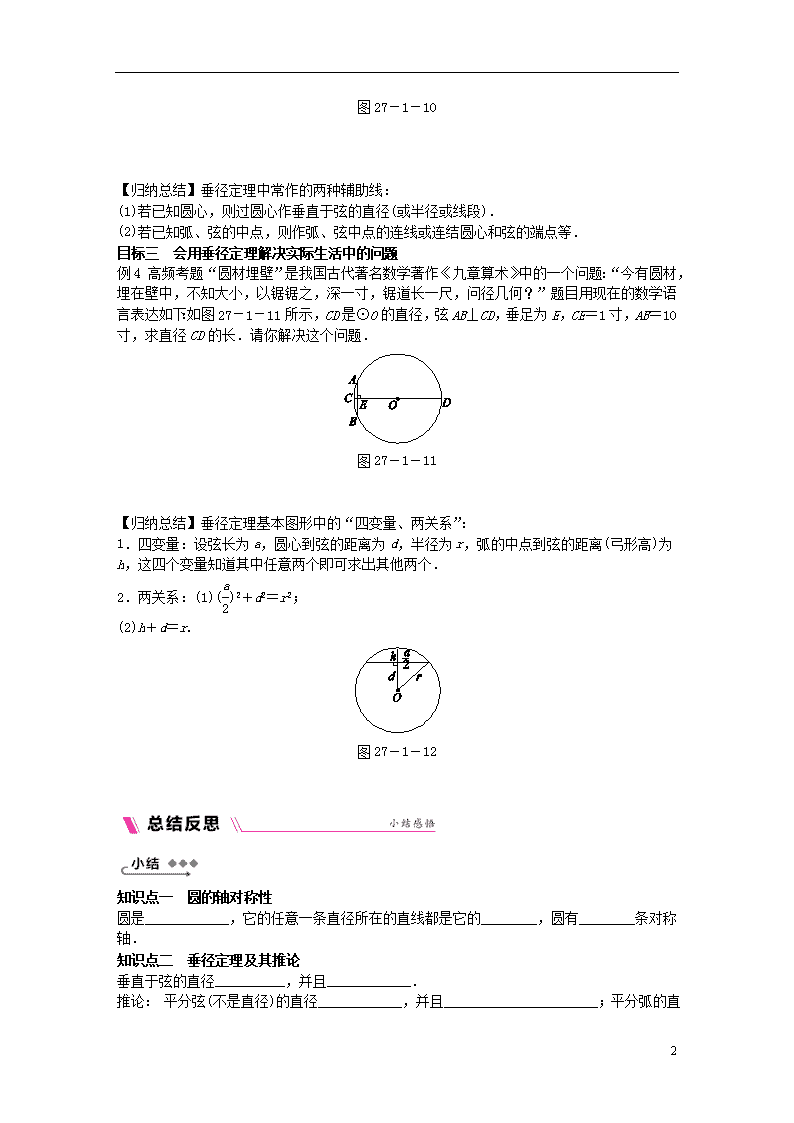
例4 高频考题“圆材埋壁”是我国古代著名数学著作《九章算术》中的一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”题目用现在的数学语言表达如下:如图27-1-11所示,CD是⊙O的直径,弦AB⊥CD,垂足为E,CE=1寸,AB=10寸,求直径CD的长.请你解决这个问题.
图27-1-11
【归纳总结】垂径定理基本图形中的“四变量、两关系”:
1.四变量:设弦长为a,圆心到弦的距离为d,半径为r,弧的中点到弦的距离(弓形高)为h,这四个变量知道其中任意两个即可求出其他两个.
2.两关系:(1)()2+d2=r2;
(2)h+d=r.
图27-1-12
知识点一 圆的轴对称性
圆是____________,它的任意一条直径所在的直线都是它的________,圆有________条对称轴.
知识点二 垂径定理及其推论
垂直于弦的直径__________,并且____________.
推论: 平分弦(不是直径)的直径____________,并且______________________
4
;平分弧的直径垂直平分这条弧所对的弦.
已知CD是⊙O的一条弦,作直径AB,使AB⊥CD,垂足为E,若AB=10,CD=8,求BE的长.
解:如图27-1-13,连结OC,则OC=5.
∵AB是⊙O的直径,AB⊥CD,
∴CE=CD=4.
在Rt△OCE中,
OE==3,
∴BE=OB+OE=5+3=8. 图27-1-13
以上解答过程完整吗?若不完整,请进行补充.
4
教师详解详析
【目标突破】
例1 [解析] C 因为对称轴是直线,不是线段,而圆的直径是线段,故A不正确;因为圆的对称轴有无数条,故B不正确;因为圆的对称轴是直径所在的直线,所以一定经过圆心,故D不正确,C正确.故选C.
例2 [解析] D ∵AB是⊙O的直径,弦CD⊥AB,垂足为M,∴M为CD的中点,即CM=DM,故选项A成立;由垂径定理可得=,故选项B成立;在△ACM和△ADM中,∵AM=AM,∠AMC=∠AMD=90°,CM=DM,∴△ACM≌△ADM,∴∠ACD=∠ADC,故选项C成立;而OM与MB不一定相等,故选项D不成立.故选D.
例3 解:(1)证明:∵AB是⊙O的直径,CD为弦,AB⊥CD,∴=,∴BC=BD.
(2)如图,连结OC.
∵AB是⊙O的直径,CD为弦,AB⊥CD,CD=6,∴CH=3,
∴OC===,
故⊙O的半径为.
例4 [解析] 连结OA,构造Rt△AOE,利用勾股定理及垂径定理解答.
解:连结OA.
∵CD⊥AB于点E,CD为⊙O的直径,
∴AE=AB=×10=5(寸).
在Rt△AEO中,设AO=x寸,
则OE=(x-1)寸.
由勾股定理,得x2=52+(x-1)2,
解得x=13.
∴AO=13寸,∴CD=2AO=26寸.
答:直径CD的长为26寸.
【总结反思】
[小结] 知识点一 轴对称图形 对称轴 无数
知识点二 平分这条弦 平分这条弦所对的两条弧 垂直于这条弦 平分这条弦所对的两条弧
[反思]
不完整.补充如下:
如图,当垂足E在线段OB上时,
此时,BE=OB-OE=5-3=2.
∴BE的长为8或2.
4
相关文档
- 2020九年级数学下册 第26章 二次函2021-04-13 21:20:064页
- 人教版数学中考复习课件第三章第四2021-04-13 18:57:4761页
- 江西专版2020中考数学复习方案第三2021-04-13 02:08:127页
- 江西专版2020中考数学复习方案第三2021-02-26 22:23:2340页
- 2020中考数学高分一轮复习教材同步2021-02-26 21:11:401页
- 江西专版2020中考数学复习方案第三2021-02-26 20:44:1343页
- 【教材梳理+中考夺分】初中数学中2021-02-26 19:33:1446页
- 福建专版2020中考数学复习方案第三2021-02-26 19:01:217页
- 2020九年级数学下册 二次函数的图2021-02-26 18:51:536页