- 746.72 KB
- 2021-02-26 发布
第
12
课时
二次函数的图象与性质
(
一
)
第三单元 函数
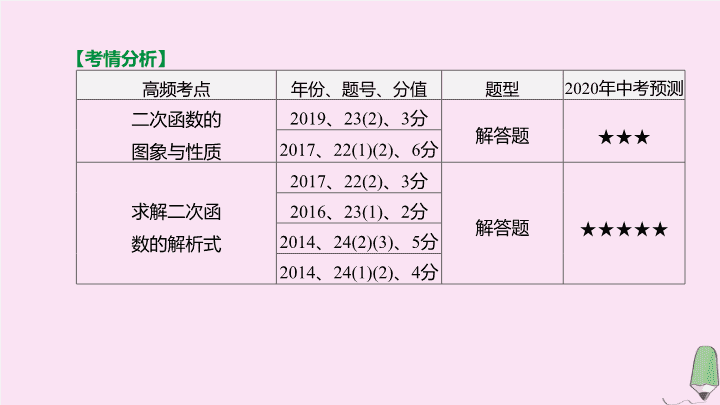
【
考情分析
】
高频考点
年份、题号、分值
题型
2020
年中考预测
二次函数的
图象与性质
2019
、
23(2)
、
3
分
解答题
★★★
2017
、
22(1)(2)
、
6
分
求解二次函
数的解析式
2017
、
22(2)
、
3
分
解答题
★★★★★
2016
、
23(1)
、
2
分
2014
、
24(2)(3)
、
5
分
2014
、
24(1)(2)
、
4
分
考点一 二次函数的概念
考点聚焦
一般地
,
形如
①
(
a
,
b
,
c
是常数
,
a
≠0)
的函数
,
叫做二次函数
.
y=ax
2
+
bx
+
c
【
温馨提示
】
函数
y=ax
2
+
bx
+
c
未必是二次函数
,
当
②
时
,
y=ax
2
+
bx
+
c
是二次函数
.
a
≠0
函数
y=ax
2
+
bx
+
c
(
a
,
b
,
c
为常数
,
a
≠0)
a>
0
a<
0
图象
开口方向
开口
③
,
并向上无限延伸
开口
④
,
并向下无限延伸
对称轴
直线
⑤
顶点坐标
⑥
考点二 二次函数的图象与性质
向上
向下
(续表)
减小
增大
增大
减小
(续表)
小
大
考点三 二次函数图象的画法
考点四 二次函数的表示及解析式的求法
1
.
二次函数的三种表示方法
(1)
一般式
:
⑬
.
(2)
顶点式
:
y=a
(
x
-
h
)
2
+
k
(
a
≠0),
其中二次函数图象的顶点坐标是
⑭
.
(3)
两点式
:
y=a
(
x
-
x
1
)(
x
-
x
2
)(
a
≠0),
其图象与
x
轴的交点的坐标为
⑮
.
y=ax
2
+
bx
+
c
(
a
≠0)
(
h
,
k
)
(
x
1
,0),(
x
2
,0)
2
.
二次函数解析式的确定
用待定系数法求二次函数的解析式时
,
注意解析式的设法
,
常见情况如下
:
条件
设法
顶点在原点
y=ax
2
(
a
≠0)
顶点在
y
轴上
y=ax
2
+
c
(
a
≠0,
y
轴为对称轴
)
顶点在
x
轴上
y=a
(
x
-
h
)
2
(
a
≠0,
直线
x=h
是对称轴
)
抛物线过原点
y=ax
2
+
bx
(
a
≠0)
顶点
(
h
,
k
)
y=a
(
x
-
h
)
2
+
k
(
a
≠0)
抛物线与
x
轴的
交点
为
(
x
1
,0),(
x
2
,0)
y=a
(
x
-
x
1
)(
x
-
x
2
)(
a
≠0)
考点五 二次函数图象的平移
抛物线
y=ax
2
+
bx
+
c
(
a
≠0)
可用配方法化成
y=a
(
x
-
h
)
2
+
k
(
a
≠0)
的形式
,
任意抛物线
y=a
(
x
-
h
)
2
+
k
(
a
≠0)
均可由抛物线
y=ax
2
(
a
≠0)
平移得到
,
具体平移方法如图
12-1 (
假设
h
,
k
均为正数
):
图
12-1
【
温馨提示
】
平移规则为
“
上加下减
,
左加右减
”
.
题组一 必会题
对点演练
A
2
.
[2019·
遂宁
]
二次函数
y=x
2
-
ax
+
b
的图象如图
12-2,
对称轴为直线
x=
2,
下列结论不正确的是
(
)
A
.a=
4
B
.
当
b=
-4
时
,
顶点的坐标为
(2,-8)
C
.
当
x=
-1
时
,
b>
-5
D
.
当
x>
3
时
,
y
随
x
的增大而增大
C
图
12-2
3
.
[2019·
温州
]
已知二次函数
y=x
2
-4
x
+2,
关于该函数在
-1≤
x
≤3
的取值范围内
,
下列说法正确的是
(
)
A
.
有最大值
-1,
有最小值
-2
B
.
有最大值
0,
有最小值
-1
C
.
有最大值
7,
有最小值
-1
D
.
有最大值
7,
有最小值
-2
4
.
[2019·
陇南
]
将二次函数
y=x
2
-4
x
+5
化成
y=a
(
x
-
h
)
2
+
k
的形式为
.
D
y=
(
x
-2)
2
+1
题组二 易错题
【
失分点
】
弄混二次函数顶点式与顶点坐标符号的关系
;
忽视二次函数的二次项系数不为
0
的条件
;
未注意二次函数的增减性与顶点横坐标和抛物线开口方向的关系
.
5
.
[2018·
潍坊
]
已知二次函数
y=
-(
x
-
h
)
2
(
h
为常数
),
当自变量
x
的值满足
2≤
x
≤5
时
,
与其对应的函数值
y
的最大值为
-1,
则
h
的值为
(
)
A
.
3
或
6 B
.
1
或
6
C
.
1
或
3 D
.
4
或
6
[
答案
] B
[
解析
]
二次函数
y=
-(
x
-
h
)
2
,
当
x=h
时
,
有最大值
0,
而当自变量
x
的值满足
2≤
x
≤5
时
,
与其对应的函数值
y
的最大值为
-1,
故
h<
2
或
h>
5
.
当
h<
2,2≤
x
≤5
时
,
y
随
x
的增大而减小
,
故当
x=
2
时
,
y
有最大值
,
此时
-(2-
h
)
2
=
-1,
解得
h
1
=
1,
h
2
=
3(
舍去
),
此时
h=
1;
当
h>
5,2≤
x
≤5
时
,
y
随
x
的增大而增大
,
故当
x=
5
时
,
y
有最大值
,
此时
-(5-
h
)
2
=
-1,
解得
h
1
=
6,
h
2
=
4(
舍去
),
此时
h=
6;
综上可知
h=
1
或
6,
故选
B
.
6
.
若
y=
(
m
-2)
x
|m|
是二次函数
,
则
m=
.
-2
7
.
已知抛物线
y=x
2
+(
m
2
-1)
x
+
m
+1
的顶点在
y
轴的正半轴上
,
则
m=
.
[
答案
] 1
[
解析
]
由题意得
m
2
-1
=
0
且
m
+1
>
0,
∴
m=
1
.
考向一 二次函数的图象与性质
【
方法点析
】
分析二次函数的增减性
,
首先需明确抛物线的开口方向
,
然后在对称轴左、右两侧分别讨论
.
|
考向精练
|
图
12-3
图
12-4
[
答案
] D
2
.
[2015·
江西
6
题
]
已知抛物线
y=ax
2
+
bx
+
c
(
a>
0)
过
(-2,0),(2,3)
两点
,
那么抛物线的对称轴
(
)
A
.
只能是直线
x=
-1
B
.
可能是
y
轴
C
.
可能在
y
轴右侧
D
.
只能在
y
轴左侧
[
答案
] D
[
答案
] D
4
.
[2019·
雅安
]
在平面直角坐标系中
,
对于二次函数
y=
(
x
-2)
2
+1,
下列说法中错误的是
(
)
A
.y
的最小值为
1
B
.
图象顶点坐标为
(2,1),
对称轴为直线
x=
2
C
.
当
x<
2
时
,
y
的值随
x
值的增大而增大
,
当
x
≥2
时
,
y
的值随
x
值的增大而减小
D
.
它的图象可以先由
y=x
2
的图象向右平移
2
个单位长度
,
再向上平移
1
个单位长度得到
C
考向二 确定二次函数的解析式
(2)
由顶点
A
(-1,4),
可设二次函数解析式为
y=a
(
x
+1)
2
+4(
a
≠0)
.
∵二次函数的图象过点
B
(2,-5),
∴
-5
=a
(2+1)
2
+4,
解得
a=
-1
.
∴二次函数的解析式是
y=
-(
x
+1)
2
+4
.
(3)
方法一
:
设二次函数的解析式为
y=a
(
x
+1)(
x
-3),
把
C
(0,-3)
代入得
a
×1×(-3)
=
-3,
解得
a=
1,
∴这个二次函数的解析式为
y=
(
x
+1)(
x
-3)
=x
2
-2
x
-3
.
【
方法点析
】
对于确定二次函数解析式问题
,
一般采用如下两种方法
,
一是待定系数法
,
在运用此法时
,
需要根据题中所给条件正确选用
“
一般式、顶点式、交点式
”
中的一种形式
,
否则会给计算带来不便
,
若条件不是直接给出
,
应作适当转化
,
使其条件满足相应的形式
,
二是由题中的数量关系或几何关系
,
直接求得两个变量之间的关系式
.
|
考向精练
|
2
.
[2017·
江西
22
题
]
已知抛物线
C
1
:
y=ax
2
-4
ax
-5(
a>
0)
.
(1)
当
a=
1
时
,
求抛物线与
x
轴的交点坐标及对称轴
.
(2)
①试说明无论
a
为何值
,
抛物线
C
1
一定经过两个定点
,
并求出这两个定点的坐标
;
②将抛物线
C
1
沿这两个定点所在直线翻折
,
得到抛物线
C
2
,
直接写出
C
2
的表达式
.
(3)
若
(2)
中抛物线
C
2
的顶点到
x
轴的距离为
2,
求
a
的值
.
解
:(1)
当
a=
1
时
,
抛物线的解析式为
y=x
2
-4
x
-5
=
(
x
-2)
2
-9,
∴对称轴为直线
x=
2
.
当
y=
0
时
,
x
-2
=
3
或
-3,
即
x=
5
或
-1
.
∴抛物线与
x
轴的交点坐标为
(-1,0)
或
(5,0)
.
图
12-5
2
.
[2017·
江西
22
题
]
已知抛物线
C
1
:
y=ax
2
-4
ax
-5(
a>
0)
.
(2)
①试说明无论
a
为何值
,
抛物线
C
1
一定经过两个定点
,
并求出这两个定点的坐标
;
②将抛物线
C
1
沿这两个定点所在直线翻折
,
得到抛物线
C
2
,
直接写出
C
2
的表达式
.
(2)
①抛物线
C
1
的解析式为
y=ax
2
-4
ax
-5,
整理得
y=ax
(
x
-4)-5
.
∵当
ax
(
x
-4)
=
0
时
,
y
恒定为
-5,
∴抛物线
C
1
一定经过两个定点
(0,-5),(4,-5)
.
②这两个定点连线为
y=
-5,
将抛物线
C
1
沿
y=
-5
翻折
,
得到抛物线
C
2
,
开口方向变了
,
但是对称轴没变
,
∴抛物线
C
2
解析式为
:
y=
-
ax
2
+4
ax
-5
.
图
12-5
2
.
[2017·
江西
22
题
]
已知抛物线
C
1
:
y=ax
2
-4
ax
-5(
a>
0)
.
(3)
若
(2)
中抛物线
C
2
的顶点到
x
轴的距离为
2,
求
a
的值
.
图
12-5
相关文档
- 2014高考金钥匙数学解题技巧大揭秘2021-02-27 09:11:3812页
- 天津历年高考试题——三角函数2021-02-27 09:11:3113页
- 2021届高考数学一轮复习新人教A版2021-02-27 09:11:2918页
- 2021年中考数学一轮单元复习19一次2021-02-27 09:10:337页
- 高一数学周周练24 三角函数图象的2021-02-27 09:10:234页
- 【北师大版】2021版高考数学一轮复2021-02-27 09:10:218页
- 浙教版数学八年级下册《反比例函数2021-02-27 09:10:113页
- 高考数学一轮复习讲义—6函数与方2021-02-27 09:10:0816页
- 2020中考数学复习 第16课时 二次函2021-02-27 09:09:513页
- 2018届二轮复习专题五函数第1课时2021-02-27 09:09:4463页