2019届高三数学第二十次考试试题 理 新人教版 12页

‎2019届高三第二十次考试 理数试题 第Ⅰ卷（共60分）‎ 一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.‎ ‎1.若复数满足，其中为虚数单位，则共轭复数（ ）‎ A． B． C． D．‎ ‎2.命题，命题，真命题的是（ ）‎ A． B． C． D．‎ ‎3.若，则的值为（ ）‎ A． B． C． D． ‎ ‎4.某同学从家到学校途经两个红绿灯，从家到学校预计走到第一个红绿灯路口遇到红灯的概率为,两个红绿灯路口都遇到红灯的概率为，则在第一个路口遇到红灯的前提下，第二个路口也遇到红灯的概率为（ ）‎ A． B． C. D．‎ ‎5.已知成等差数列，成等比数列，则椭圆的离心率为（ ）‎ A． B． C. D．‎ ‎6.执行如图所示的程序框图，若输入,输出的，则空白判断框内应填的条件可能是（ ）‎ A． B． ‎ C. D．‎ - 12 -‎ ‎7.在中，，，，若，，且，则的值为（ ）‎ A． B． C. D．‎ ‎8.设，函数的图象向右平移个单位后与原图像重合，则的最小值是（ ）‎ A． B． C. 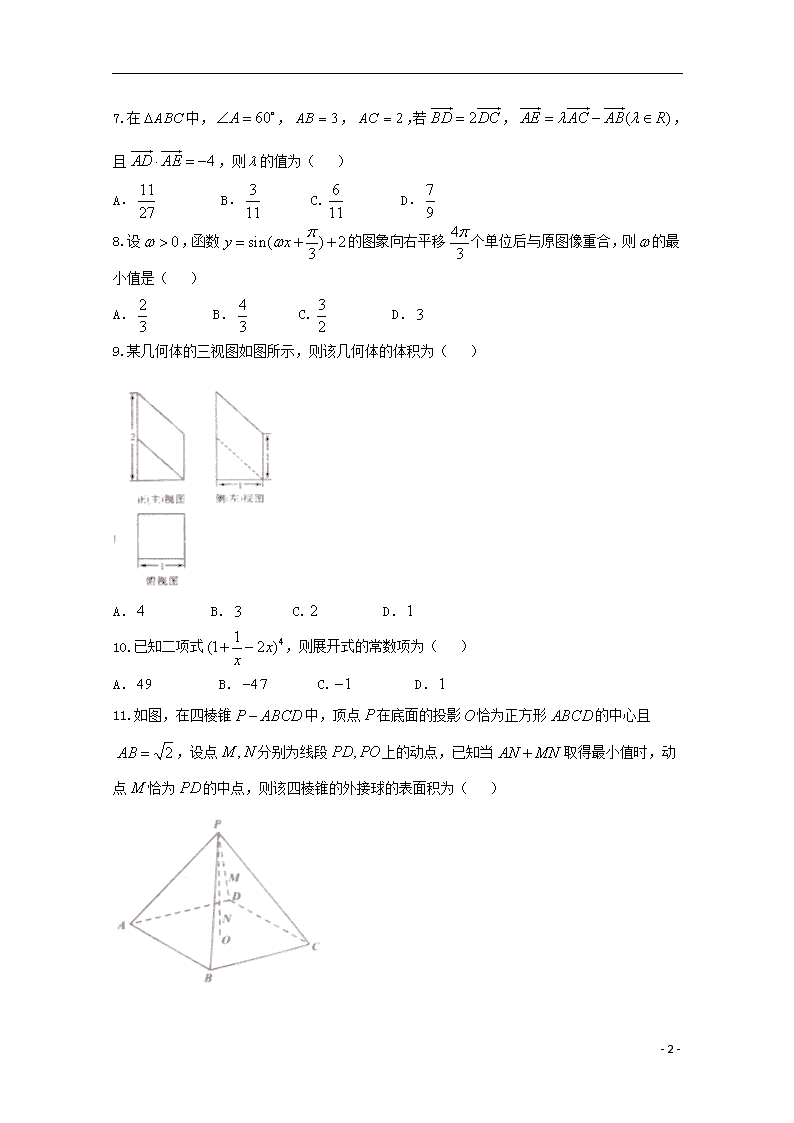D．‎ ‎9.某几何体的三视图如图所示，则该几何体的体积为（ ）‎ A． B． C. D．‎ ‎10.已知二项式，则展开式的常数项为（ ）‎ A． B． C. D．‎ ‎11.如图，在四棱锥中，顶点在底面的投影恰为正方形的中心且，设点分别为线段上的动点，已知当取得最小值时，动点恰为的中点，则该四棱锥的外接球的表面积为（ ）‎ - 12 -‎ A． B． C. D．‎ ‎12.已知函数，若有且仅有两个整数，使得，则的取值范围为（ ）‎ A． B． C. D．‎ 第Ⅱ卷（共90分）‎ 二、填空题（每题5分，满分20分，将答案填在答题纸上）‎ ‎13.若函数为偶函数，则 ．‎ ‎14.已知双曲线的离心率为，左焦点为，当点在双曲线右支上运动、点在圆上运动时，则的最小值为 ．‎ ‎15.若满足，则的最大值为 ．‎ ‎16.已知为锐角的外心，，若，且，记，则的大小关系为 ．‎ 三、解答题 （本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.） ‎ ‎17.各项均为正数的数列的前项和为，满足，‎ 各项均为正数的等比数列满足 ‎（1）求数列的通项公式；‎ ‎（2）若，数列的前项和，求.‎ ‎18.如图，在三棱柱中，侧面为菱形，，‎ ‎（1）求证：平面平面，‎ ‎（2）若，，，求异面直线与所成角的余弦值.‎ - 12 -‎ ‎ ‎ ‎19. 某工厂每日生产一种产品吨，每日生产的产品当日销售完毕，日销售额为万元，产品价格随着产量变化而有所变化，经过段时间的产销， 得到了的一组统计数据如下表:‎ 日产量 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ 日销售量 ‎5‎ ‎12‎ ‎16‎ ‎19‎ ‎21‎ ‎（1）请判断与中，哪个模型更适合到画之间的关系？可从函数增长趋势方面给出简单的理由；‎ ‎（2）根据你的判断及下面的数据和公式，求出关于的回归方程，并估计当日产量时，日销售额是多少?‎ 参考数据：，‎ 线性回归方程中，，，‎ ‎20. 如图，设抛物线的准线与轴交于椭圆的右焦点，为左焦点，椭圆的离心率为，抛物线与椭圆交于轴上方一点，连接并延长交于点为上一动点，且在之间移动.‎ ‎（1）当取最小值时，求和的方程；‎ - 12 -‎ ‎（2）若的边长恰好是三个连接的自然数，求面积的最大值.‎ ‎21.已知函数.‎ ‎（1）当时，恒成立，求实数的取值范围；‎ ‎（2）证明：当时，函数有最小值，设最小值为，求函数的值域.‎ 请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分.‎ ‎22.选修4-4：坐标系与参数方程 在直角坐标系中，曲线过点，其参数方程为，(为参数)。以坐标原点为极点，轴的非负半轴为极轴，建立极坐标系，曲线的极坐标方程为.‎ ‎（1）求曲线的普通方程和曲线的直角坐标方程；‎ ‎（2）若曲线与相交于两点，求的值。‎ ‎23.选修4-5：不等式选讲 已知函数，其中.‎ ‎（1）当时，求不等式的解集；‎ ‎（2）已知关于的不等式的解集为，求的值.‎ - 12 -‎ ‎20次考试理数参考答案 一、选择题 ‎1-5:CCABA 6-10:BBCDD 11、12：AB 二、填空题 ‎13. 或 14. 15. 16.‎ 三、解答题 ‎17.（1） ‎ ‎∴‎ ‎∴‎ 又各项为正 ‎∴‎ ‎∴为公差为的等差数列 ‎∴‎ ‎ ‎ ‎∴‎ ‎（2）‎ ‎∴‎ - 12 -‎ ‎18.解：（1）证明：∵四边形为菱形，‎ ‎∴‎ ‎∴平面，‎ ‎∴底面.‎ ‎∵平面，‎ ‎∴平面平面.‎ ‎（2）解：连接，‎ ‎∵四边形为菱形，‎ ‎∴为的中点.‎ ‎∵‎ ‎∴‎ 在菱形中，‎ ‎∴为等边三角形,‎ ‎∴‎ ‎∴，即 ‎∵平面平面 ‎∴面 ‎∴‎ ‎∴垂直平分 ‎∴，‎ ‎∵‎ ‎∴‎ ‎∵‎ ‎∴是异面直线与所成角（或其补角）‎ 在中，，‎ - 12 -‎ ‎∴异面直线与所成角的余弦值为 ‎19.（1）更适合刻画之间的关系， ‎ 理由如下: 值每增加，函数值的增加量分别为，增加得越来越缓慢，适合对数型函数的增长规律，与直线型函数的均匀增长存在较大差异，故更适合刻画间的关系 ‎ ‎（2）令，计算知 所以 ‎.‎ 所以所求的回归方程为 当时，销售额为(万元) ‎ ‎20.解（1）因为，，‎ 则，，‎ 所以取最小值时，‎ 此时抛物线，此时，‎ 所以椭圆的方程为.‎ - 12 -‎ ‎（2）因为，，则，，‎ 设椭圆的标准方程为，，，‎ 由，得，‎ 所以或（舍去），‎ 代入抛物线方程得，‎ 即，‎ 于是，，‎ 又的边长恰好是三个连续的自然数，‎ 所以，此时抛物线方程为，‎ 则直线的方程为，‎ 联立，得或（舍去）‎ 于是.‎ 所以，‎ 设到直线的距离为，‎ 则 当时，，‎ - 12 -‎ 所以的面积最大值为.‎ ‎21.解：（1）因为对恒成立，‎ 等价于对恒成立，‎ 设 得，‎ 故在上单调递增，‎ 当时，由上知，‎ 所以，‎ 即.‎ 所以实数的取值范围为；‎ ‎（2）对求导得 记 ‎ 由（1）知在区间内单调递增，‎ 又，‎ 所以存在唯一正实数，‎ 使得，‎ ‎∴当时，，函数在区间单调递减；‎ 时，，函数在区间单调递增；‎ - 12 -‎ 所以在内有最小值，‎ 有题设即，‎ 又因为，‎ 所以 根据（1）知，在内单调递增，，‎ 所以，‎ 令，‎ 则，‎ 函数在区间内单调递增，‎ 所以，‎ 即函数的值域为.‎ ‎22.解（1）由（为参数）‎ 可得的普通方程为，‎ 又的极坐标方程为，‎ 即 所以的直角坐标方程为,‎ ‎（2）的参数过程可化为（为参数），‎ - 12 -‎ 代入得：，‎ 设对应的直线的参数分别为，‎ ‎，‎ 所以，‎ 所以 ‎23.（1）当时，‎ 当时，由得，解得；‎ 当时，由得无解；‎ 当时，由得，解得，‎ 故不等式的解集或 ‎（2）令，‎ 则 由，解得，‎ 又知的解集为，‎ 所以 于是解得 ‎ - 12 -‎