- 1.01 MB
- 2023-11-20 发布
2010年普通高等学校招生全国统一考试(天津卷)
数学 (理工类)
本试卷分为第I卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试用时120分钟,第I卷1至3页,第Ⅱ卷4至11页。考试结束后,将本试卷和答题卡一并交回。
第I卷
注意事项:
1. 答第I卷前,考生务必将自己的姓名、准考号填写在答题卡上,并在规定位置粘贴考试用条形码。
2. 每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其他答案标号。答在试卷上的无效。
3. 本卷共10小题,每小题5分,共50分。
参考公式:
·如果事件A,B互斥,那么 ·如果事件A,B相互独立,那么
P(AB)=P(A)+P(B). P(AB)=P(A)P(B).
·棱柱的体积公式V=Sh. ·棱锥的体积公式V=Sh.
其中S表示棱柱的底面积, 其中S表示棱锥的底面积.
H表示棱柱的高 h表示棱锥的高.
一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.
(1)i是虚数单位,复数=
(A)1+i (B)5+5i (C)-5-5i (D)-1-i
(2)函数的零点所在的一个区间是
(A)(-2,-1) (B)(-1,0) (C)(0,1) (D)(1,2)
(3)命题“若是奇函数,则是奇函数”的否命题是
(A)若是偶函数,则是偶函数
(B)若是奇数,则不是奇函数
(C)若是奇函数,则是奇函数
(D)若是奇函数,则不是奇函数
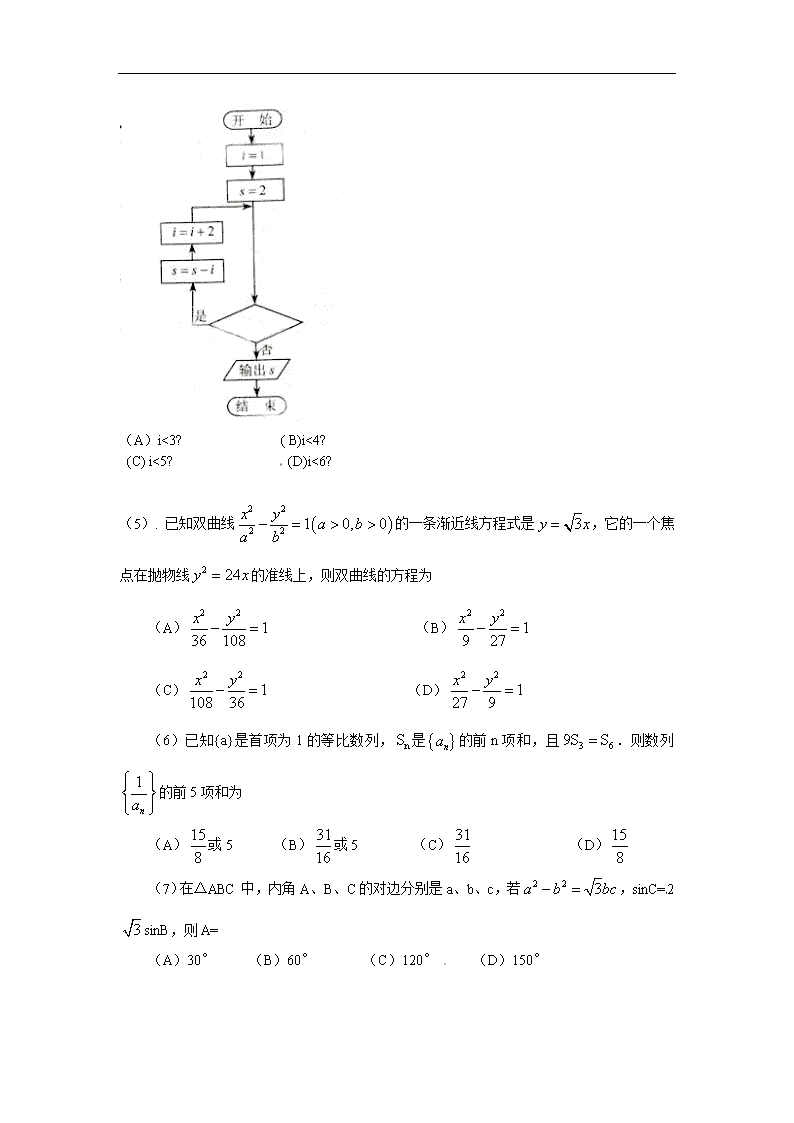
(4)阅读右边的程序框图,若输出S的值为-7,则判断框内可填写
(A)i<3? ( B)i<4?
(C) i<5? (D)i<6?
(5). 已知双曲线的一条渐近线方程式是,它的一个焦点在抛物线的准线上,则双曲线的方程为
(A) (B)
(C) (D)
(6)已知{a}是首项为1的等比数列,是的前n项和,且.则数列的前5项和为[来源:
(A)或5 (B)或5 (C) (D)
(7)在△ABC中,内角A、B、C的对边分别是a、b、c,若,sinC=2sinB,则A=
(A)30° (B)60° (C)120° (D)150°
(8)设函数f(x)= 若,则实数的取值范围是
(A) (B) [来源:学科网]
(C) (D)
(9)设集合A=,B=.若,则实数必满足
(A) (B)
(C) (D)
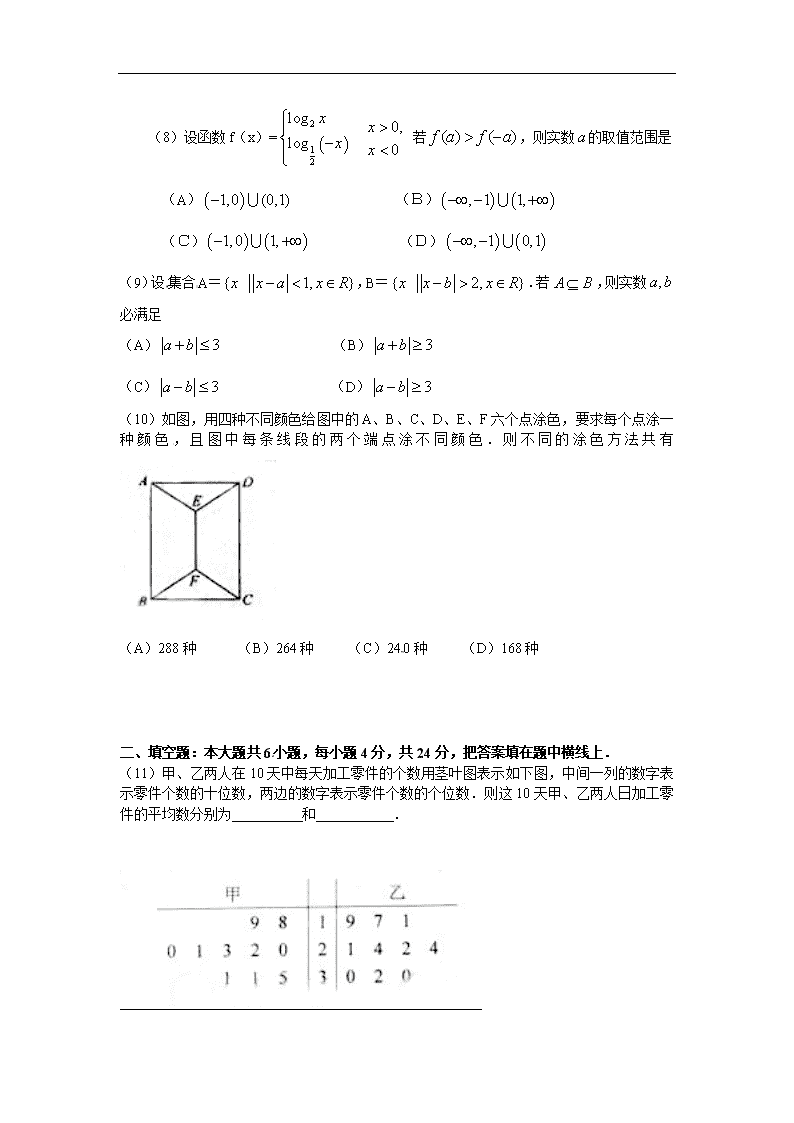
(10)如图,用四种不同颜色给图中的A、B、C、D、E、F六个点涂色,要求每个点涂一种颜色,且图中每条线段的两个端点涂不同颜色.则不同的涂色方法共有
(A)288种 (B)264种 (C)240种 (D)168种
二、填空题:本大题共6小题,每小题4分,共24分,把答案填在题中横线上.
(11)甲、乙两人在10天中每天加工零件的个数用茎叶图表示如下图,中间一列的数字表示零件个数的十位数,两边的数字表示零件个数的个位数.则这10天甲、乙两人日加工零件的平均数分别为 和 .
(12 ) 一个几何体的三视图如图所示,则这个几何体的体积为 .
(13)已知圆C的圆心是直线(为参数)与轴的交点,且圆C与直线相切.则圆C的方程为 .
(14)如图,四边形ABCD是圆O的内接四边形,延长AB和DC相交于点P.若,,则的值为 .
(15)如图,在中,,,则= .
(16)设函数,对任意, 恒成立,则实数m的取值范围是 .
三、解答题:本大题共6小题,共76分。解答应写出文字说明,证明过程或演算步骤。
(17)(本小题满分12分)
已知函数=2.
(Ⅰ)求函数的最小正周期及在区间上的最大值和最小值;
(Ⅱ)若,,求的值.
(18)(本小题满分12分)[来源:Zxxk.Com]
某射手每次射击击中目标的概率是,且各次射击的结果互不影响.
(Ⅰ)假设这名射手射击5次,求恰有2次击中目标的概率;
(Ⅱ)假设这名射手射击5次,求有3次连续击中目标,另外2次未击中目标的概率;
(Ⅲ)假设这名射手射击3次,每次射击,击中目标得1分,未击中目标得0分.在3次射击中,若有2次连续击中,而另外1次未击中,则额外加1分;若3次全击中,则额外加3分.记ξ为射手射击3次后的总得分数,求ξ的分布列.
(19)(本小题满分12分)
如图,在长方体中,分别是棱,上的点,,.
(Ⅰ)求异面直线与所成角的余弦值;
(Ⅱ)证明⊥平面;
(Ⅲ) 求二面角的正弦值.
(20)(本小题满分12分)
已知椭圆(>>0)的离心率,连接椭圆的四个顶点得到的菱形的面积为4.
(Ⅰ)求椭圆的方程;
(Ⅱ)设直线与椭圆相交于不同的两点.已知点的坐标为(-,0),点(0,)在线段的垂直平分线上,且=4.求的值.
(21)(本小题满分14分)
已知函数.
(Ⅰ) 求函数f(x)的单调区间和极值;
(Ⅱ)已知函数y=g(x)的图象与函数y=f(x)的图象关于直线x=1对称.证明当x>1时,f(x)>g(x);
(Ⅲ)如果且证明.
(22)(本小题满分14分)
在数列中,,且说对任意,成等差数列,其公差为.
(Ⅰ)若=2k,证明成等比数列();
(Ⅱ)若对任意,成等比数列,其公比为.
(i)设1.证明是等差数列;
(ii)若,证明.
2010年普通高等学校招生全国统一考试(天津卷)
数学(理工类)参考解答
三、解答题
(17)本小题主要考查二倍角的正弦与余弦、两角和的正弦、函数的性质、同角三角函数的基本关系、两角差的余弦等基础知识,考查基本运算能力.满分12分.
(Ⅰ)解:由,得
.
所以函数的最小正周期为.
因为在区间上为增函数,在区间上为减函数,又
,所以函数在区间上的最大值为2,最小值为-1.
(Ⅱ)解:由(Ⅰ)可知.
又因为,所以.
由,得.
(18)本小题主要考查二项分布及其概率计算公式、离散型随机变量的分布列、互斥事件和相互独立事件等基础知识,考查运用概率知识解决实际问题的能力.满分12分.
(Ⅰ)解:设为射手在5次射击中击中目标的次数,则.在5次射击中,恰有2次击中目标的概率
.
(Ⅱ)解:设“第次射击击中目标”为事件;“射手在5次射击中,有3次连续击中目标,另外2次未击中目标”为事件,则
=
=.
(Ⅲ)解:由题意可知,的所有可能取值为.
;
=;
;
(19)本小题主要考查异面直线所成的角、直线与平面垂直、二面角等基础知识,考查用空间向量解决立体几何问题的方法,考查空间想象能力、运算能力和推理论证能力.满分12分.
方法一:如图所示,建立空间直角坐标系,
点A为坐标原点.设,依题意得,
,,.
(Ⅰ)解:易得,.
于是.
所以异面直线与所成角的余弦值为.
(Ⅱ)证明:已知,,.
于是·=0,·=0.因此,,.又.
所以平面.
(Ⅲ)解:设平面的法向量,则,即.
方法二:(Ⅰ)解:设AB=1,可得AD=2,AA1=4,CF=1,CE=.
连接B1C,BC1,设B1C与BC1交于点M.易知A1D∥B1C.由,可知EF∥BC1.故是异面直线EF与A1D所成的角.易知BM=CM=,所以[来源:Z_xx_k.Com]
.
所以异面直线FE与A1D所成角的余弦值为.
(Ⅱ)证明:连接AC,设AC与DE交点N.
因为,所以.
从而.又由于,所以.
故AC⊥DE.又因为CC1⊥DE且,所以DE⊥平面ACF.从而AF⊥DE.
连接BF,同理可证B1C⊥平面ABF,从而AF⊥B1C,所以AF⊥A1D.因为,所以AF⊥平面A1ED.
(Ⅲ)解:连接A1N,FN.由(Ⅱ)可知DE⊥平面ACF.又NF平面ACF, A1N平面ACF,所以DE⊥NF,DE⊥A1N,故为二面角A1-ED-F的平面角.
易知,所以.又,所以.在中.在中,.
连接A1C1,A1F. 在.
在中,.所以.
所以二面角A1-DE-F正弦值为.
由得
设线段AB的中点为M,则M的坐标为
以下分两种情况:
(1)当k=0时,点B的坐标为(2,0),线段AB的垂直平分线为y轴,于是
(21)本小题主要考查导数的运算、利用导数研究函数的单调性与极值等基础知识,考查运算能力及用函数思想分析解决问题的能力,满分14分[来源:学|科|网]
(Ⅰ)解:
令,解得x=1
当x变化时,,的变化情况如下表
X
()
1
()
+
0
-
极大值
所以在()内是增函数,在()内是减函数.
函数在x=1处取得极大值f(1)且f(1)=
(Ⅱ)证明:由题意可知g(x)=f(2-x),得g(x)=(2-x)
令F(x)=f(x)-g(x),即
(Ⅲ)证明:(1)
若,由(Ⅰ)及,得与矛盾
(2)若,由(Ⅰ)及,得与矛盾
根据(1)(2)得
由(Ⅱ)可知,>,则=,所以>,从而>.因为,所以,又由(Ⅰ)可知函数f(x)在区间(-∞,1)内是增函数,所以>,即>2.
(22)本小题主要考查等差数列的定义及通项公式,前n项和公式、等比数列的定义、数列求和等基础知识,考查运算能力、推理论证能力、综合分析和解决问题的能力及分类讨论的思想方法.满分14分.
(Ⅰ)证明:由题设,可得
所以
由=0,得从而
于是.
所以成等比数列.
(Ⅱ)证法一:(i)证明:由成等差数列,及
成等比数列,得
当≠1时,可知≠1,k
从而,即,
所以是等差数列,公差为1.[来源:Zxxk.Com]
(ii)证明:由,,可得,从而=1.由(i)有
,得
+
所以,从而
(2)当n为奇数时,设n=2m+1()
所以从而···
综合(1)和(2)可知,对任意,,有
(ii)证明:因为所以.
所以,从而,.于是,由(i)可知是公差为1的等差数列.由等差数列的通项公式可得=,故.
从而.
所以,由,可得
.
于是,由(Ⅰ)可知
以下同证法一.