高中数学必修1教案：第五章（第8课时）线段的定比分点 7页

课 题：线段的定比分点 教学目的：‎ ‎1掌握线段的定比分点坐标公式及线段的中点坐标公式；‎ ‎2熟练运用线段的定比分点坐标公式及中点坐标公式；‎ ‎3理解点P分有向线段所成比λ的含义；‎ ‎4明确点P的位置及λ范围的关系 教学重点：线段的定比分点和中点坐标公式的应用 教学难点：用线段的定比分点坐标公式解题时区分λ＞0还是λ＜０‎ 授课类型：新授课 课时安排：1课时 教 具：多媒体、实物投影仪 教学过程：‎ 一、复习引入：‎ ‎1向量的加法：求两个向量和的运算，叫做向量的加法 向量加法的三角形法则和平行四边形法则 ‎2．向量加法的交换律：+=+‎ ‎3．向量加法的结合律：(+) +=+ (+)‎ ‎4．向量的减法向量a加上的b相反向量，叫做a与b的差即：a - b = a + (-b) ‎ ‎5．差向量的意义： = a, = b, 则= a - b ‎ 即a - b可以表示为从向量b的终点指向向量a的终点的向量 ‎6．实数与向量的积：实数λ与向量的积是一个向量，记作：λ ‎（1）|λ|=|λ|||；（2）λ>0时λ与方向相同；λ<0时λ与方向相反；λ=0时λ=‎ ‎7．运算定律 λ(μ)=(λμ)，(λ+μ)=λ+μ，λ(+)=λ+λ ‎ ‎8． 向量共线定理 向量与非零向量共线的充要条件是：有且只有一个非零实数λ，使=λ ‎9．平面向量基本定理：如果，‎ 是同一平面内的两个不共线向量，那么对于这一平面内的任一向量，有且只有一对实数λ1，λ2使=λ1+λ2‎ ‎(1)我们把不共线向量ｅ１、ｅ２叫做表示这一平面内所有向量的一组基底；‎ ‎(2)基底不惟一，关键是不共线；‎ ‎(3)由定理可将任一向量ａ在给出基底ｅ１、ｅ２的条件下进行分解；‎ ‎(4)基底给定时，分解形式惟一 λ1，λ2是被，，唯一确定的数量 ‎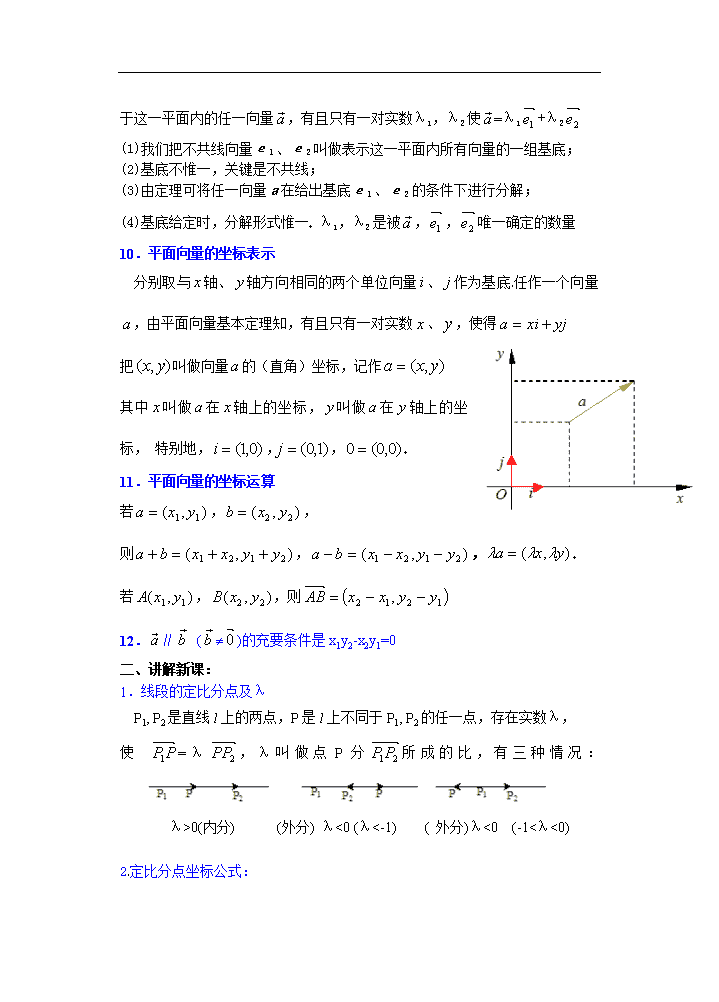10．平面向量的坐标表示 ‎ 分别取与轴、轴方向相同的两个单位向量、作为基底任作一个向量，由平面向量基本定理知，有且只有一对实数、，使得 把叫做向量的（直角）坐标，记作 其中叫做在轴上的坐标，叫做在轴上的坐标， 特别地，，，‎ ‎11．平面向量的坐标运算 若，，‎ 则，，‎ 若，，则 ‎12．∥ (¹)的充要条件是x1y2-x2y1=0‎ 二、讲解新课：‎ ‎1．线段的定比分点及λ ‎ P1, P2是直线l上的两点，P是l上不同于P1, P2的任一点，存在实数λ，‎ 使 =λ，λ叫做点P分所成的比，有三种情况：‎ λ>0(内分) (外分) λ<0 (λ<-1) ( 外分)λ<0 (-1<λ<0)‎ ‎2定比分点坐标公式：‎ 若点P１(x1,y1) ，Ｐ２(x2,y2)，λ为实数，且＝λ，则点P的坐标为（），我们称λ为点P分所成的比 设=λ 点P1, P, P2坐标为(x1,y1) (x,y) (x2,y2)，由向量的坐标运算 ‎ =(x-x1,y-y1) ，=( x2-x, y2-y)‎ ‎ ∵=λ ∴ (x-x1,y-y1) =λ( x2-x, y2-y)‎ ‎ ∴ 定比分点坐标公式()‎ 点P分所成的比与点P分所成的比是两个不同的比，要注意方向 ‎3点P的位置与λ的范围的关系：‎ ‎①当λ＞０时，与同向共线，这时称点P为的内分点 特别地，当λ＝１时，有＝，即点P是线段Ｐ１Ｐ２之中点，其坐标为（）‎ ‎②当λ＜０()时，与反向共线，这时称点P为的外分点 探究：若Ｐ１、Ｐ２是直线上的两点，点P是上不同于Ｐ１、Ｐ２的任意一点，则存在一个实数λ，使＝λ，λ叫做P分有向线段所成的比 而且，当点P在线段Ｐ１Ｐ２上时，λ＞０；当点P在线段Ｐ１Ｐ２或Ｐ2Ｐ1的延长线上时，λ＜０‎ 对于上述内容，逆过来是否还成立呢?‎ ‎(1)若λ＞０，则点P为线段Ｐ１Ｐ２的内分点；‎ ‎(2)若λ＜０，则点P为线段Ｐ１Ｐ２的外分点 一般来说，(1)是正确的，而(2)却不一定正确这是因为，当λ＝－１时，定比分点的坐标公式ｘ＝和ｙ＝‎ 显然都无意义，也就是说，当λ＝－１时，定比分点不存在 由此可见，当点P为线段Ｐ１Ｐ２的外分点时，应有λ＜０且λ≠－１‎ ‎4线段定比分点坐标公式的向量形式：‎ 在平面内任取一点O，设＝ａ，＝ｂ，‎ 由于＝－＝－ａ，＝－＝ｂ－‎ 且有＝λ，所以 -a=λ(b-)即可得 ‎=‎ 这一结论在几何问题的证明过程中应注意应用 三、讲解范例：‎ 例1已知A(1，3)，B(－２，０)，Ｃ（２，１）为三角形的三个顶点，L、M、N分别是BC、CA、AB上的点，满足BL∶BC＝CM∶CA＝NA∶AB＝１∶３，求L、M、N三点的坐标 分析：所给线段长度的比，实为相应向量模的比，故可转换所给比值为点L、M、N分向量、、所成的比，由定比分点坐标公式求三个点的坐标 另外，要求L、M、N的坐标，即求、、的坐标(这里O为坐标原点)，为此，我们可借用定比分点的向量形式 下面给出第二种解法 解：∵Ａ（１，３），Ｂ（－２，０），Ｃ（２，１），‎ ‎∴＝（１，３），＝（－２，０），＝（２，１）‎ 又∵ＢＬ∶ＢＣ＝ＣＭ∶ＣＡ＝ＡＮ∶ＡＢ＝１∶３‎ ‎∴可得：L分，M分，N分所成的比均为λ＝２‎ ‎∴＝＋＝（２，１）＋（-2，0）=（-，）‎ ‎=+ = (1,3)+ （２，１）＝（，）‎ ‎＝＋＝（－２，０）＋（１，３）＝（０，２）‎ ‎∴Ｌ（－，）、Ｍ（，）、Ｎ（０，２）为所求 上述两种解题思路，各有特色，各有侧重，望同学们比较选择，灵活应用 例2已知三点A(0，8)，B(－４，０)，Ｃ（５，－３），Ｄ点内分的比为１∶３，E点在BC边上，且使△BDE的面积是△ABC面积的一半，求DE中点的坐标 分析：要求DE中点的坐标，只要求得点D、E的坐标即可，又由于点E在BC上，△BDE与△ABC有公共顶点B，所以它们的面积表达式选定一公用角可建立比例关系求解 解：由已知有＝，则得＝‎ 又，而Ｓ△ＢＤＥ＝｜｜·｜｜·sin∠DBE，‎ Ｓ△ＡＢＣ＝｜｜·｜｜sin∠ABC，且∠DBE＝∠ABC ‎ ‎∴，即得：‎ 又点E在边BC上，所以，∴点E分成比λ＝２‎ 由定比分点坐标公式有 ‎,即Ｅ（２，－２），‎ 又由 ‎,有D（－１，６）‎ 记线段DE的中点为M(x,y),则 ‎ ,即M（，２）为所求 四、课堂练习：‎ ‎1．已知点A(－２，-３)，点Ｂ（４，１），延长AB到P，使｜｜＝３｜｜，求点P的坐标 解：因为点P在AB上的延长线上，P为的外分点，所以，＝λ，λ＜０，又根据｜｜＝３｜｜，可知λ＝－３，由分点坐标公式易得P点的坐标为（７，３）．‎ ‎2．已知两点P１（３，２），Ｐ２（－８，３），求点P(，ｙ)分所成的比λ及ｙ的值 解：由线段的定比分点坐标公式得 ‎，解得 五、小结 ‎ 六、课后作业：‎ ‎1已知点A分有向线段的比为2，则在下列结论中错误的是（ ）‎ A点C分的比是-B点C分的比是-3 C点C分的比是-D点A分的比是2‎ ‎2已知两点P１（－１，－６）、Ｐ２（３，０），点P（－，ｙ）分有向线段所成的比为λ，则λ、ｙ的值为（ ）‎ A－，８ B，－８ C－，－８  D４，‎ ‎3△ABC的两个顶点A(3，7)和B(-2，5)，若AC的中点在x轴上，BC的中点在y轴上，则顶点C的坐标是（ ）‎ A(2，-7) B(-7，2) C(-3，-5) D(-5，-3)‎ ‎4已知点A(x,2),B(5,1),C(-4,2x)在同一条直线上，那么x= ‎ ‎5△ABC的顶点A(2，3)，B(-4，-2)和重心G(2，-1)，则C点坐标为 6已知M为△ABC边AB上的一点，且Ｓ△ＡＭＣ＝Ｓ△ＡＢＣ，则M分所成的比为 ‎ ‎7已知点A(-1,-4)、B(5,2)，线段AB上的三等分点依次为P１、Ｐ２，求Ｐ１、Ｐ２点的坐标以及A、B分所成的比λ．‎ ‎8过P１（１，３）、Ｐ２（７，２）的直线与一次函数的图象交于点P，求P分所成的比值 ‎9已知平行四边形ABCD一个顶点坐标为A(-2,1)，一组对边AB、CD的中点分别为M(3，0)、N(-1，-2)，求平行四边形的各个顶点坐标 参考答案：1D 2C 3A 42或 5(8,-4) 6 ‎ ‎7P1(1,-2),P2(3,0),A、B分所成的比λ1、λ2分别为-,-2 ‎ ‎8 9Ｂ（８，－１），Ｃ（４，－３），Ｄ（－６，－１） 七、板书设计（略）‎ 八、课后记： ‎