- 502.00 KB
- 2021-06-19 发布
- 1、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,可选择认领,认领后既往收益都归您。
- 2、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细先通过免费阅读内容等途径辨别内容交易风险。如存在严重挂羊头卖狗肉之情形,可联系本站下载客服投诉处理。
- 文档侵权举报QQ:3215808601
课 题:向量小结与复习(1)
教学目的:
1了解本章知识网络结构;2进一步熟悉基本概念及运算律;
3理解重要定理、公式并能熟练应用;
4加强数学应用意识,提高分析问题,解决问题的能力
5认识事物之间的相互转化;6培养学生的数学应用意识
教学重点:突出本章重、难点内容
教学难点:通过例题分析突出向量运算与实数运算的区别
授课类型:复习课
课时安排:1课时
教 具:多媒体、实物投影仪
教学方法:自学辅导法
在给出本章的知识网络结构后,列出复习提纲,引导学生补充相关内容,同时加强学生对基本概念、基本运算律、重要定理、公式的熟悉程度
教学过程:
一、引入
前面一段,我们一起学习了向量的知识以及解斜三角形问题,并掌握了一定的分析问题解决问题的方法这一节,我们开始对本章进行小结与复习
二本章知识
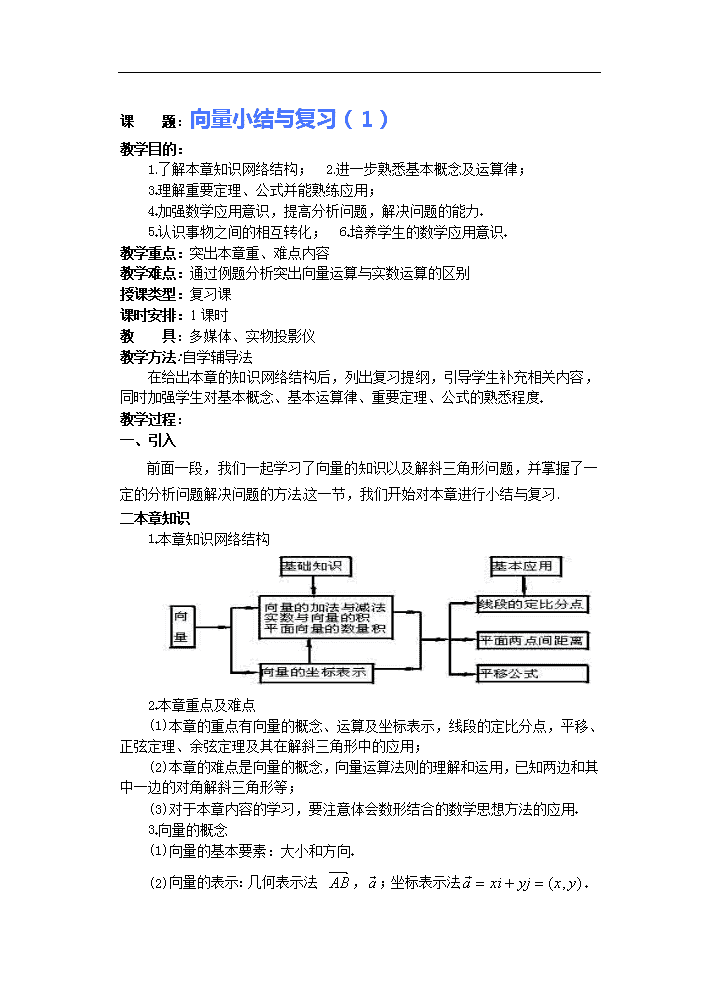
1本章知识网络结构
2本章重点及难点
(1)本章的重点有向量的概念、运算及坐标表示,线段的定比分点,平移、正弦定理、余弦定理及其在解斜三角形中的应用;
(2)本章的难点是向量的概念,向量运算法则的理解和运用,已知两边和其中一边的对角解斜三角形等;
(3)对于本章内容的学习,要注意体会数形结合的数学思想方法的应用
3向量的概念
(1)向量的基本要素:大小和方向
(2)向量的表示:几何表示法 ,;坐标表示法
(3)向量的长度:即向量的大小,记作||
(4)特殊的向量:零向量=||=0单位向量为单位向量||=1
(5)相等的向量:大小相等,方向相同
(6)平行向量(共线向量):方向相同或相反的向量,称为平行向量记作∥由于向量可以进行任意的平移(即自由向量),平行向量总可以平移到同一直线上,故平行向量也称为共线向量
4向量的运算向量的加减法,数与向量的乘积,向量的数量(内积)及其各运算的坐标表示和性质
运算类型
几何方法
坐标方法
运算性质
向
量
的
加
法
1平行四边形法则
2三角形法则
向
量
的
减
法
三角形法则
向
量
的
乘
法
1是一个向量,满足:
2>0时,与同向;
<0时,与异向;
=0时, =0
∥
向
量
的
数
是一个数
1或时,
=0
2且时,
量
积
5重要定理、公式:
(1)平面向量基本定理
是同一平面内两个不共线的向量,那么,对于这个平面内任一向量,有且仅有一对实数,使
(2)两个向量平行的充要条件
∥=λ
(3)两个向量垂直的充要条件
⊥·=O
(4)线段的定比分点公式
设点P分有向线段所成的比为λ,即=λ,则
=+ (线段的定比分点的向量公式)
(线段定比分点的坐标公式)
当λ=1时,得中点公式:
=(+)或
(5)平移公式
设点按向量平移后得到点,则=+
或,曲线按向量平移后所得的曲线的函数解析式为:
(6)正、余弦定理
正弦定理:
余弦定理:
三、讲解范例:
例1在四边形ABCD中,·=·=·=·,试证明四边形ABCD是矩形
分析:要证明四边形ABCD是矩形,可以先证四边形ABCD为平行四边形,再证明其一组邻边互相垂直为此我们将从四边形的边的长度和位置两方面的关系来进行思考
证明:设=a,=b,=c,=d,则
∵a+b+c+d=O
∴a+b=-(c+d)
两边平方得
|a|2+2a·b+|b|2=|c|2+2c·d+|d|2,
又a·b=c·d
∴|a|2+|b|2=|c|2+|d|2(1)
同理|a|+|d|2=|b|2+|c|2(2)
由(1)(2)得|a|2=|c|2,|d|2=|b|2,
∴a=c,d=b,
即AB=CD,BC=DA
∴四边形ABCD是平行四边形
于是=-,即a=-c,
又a·b=b·c,故a·b=b·(-a)
∴a·b=O
∴⊥
∴四边形ABCD为矩形
评述:向量具有二重性,一方面具有“形”的特点,另一方面又具有一套优良的运算性质,因此,对于某些几何命题的抽象的证明,自然可以转化为向量的运算问题来解决,要注意体会
例2设坐标平面上有三点A、B、C,i,j分别是坐标平面上x轴,y轴正方向的单位向量,若向量=i-2j,=i+mj,那么是否存在实数m,使A、B、C三点共线
分析:可以假设满足条件的m存在,由A、B、C三点共线∥ 存在实数λ,使=λ,从而建立方程来探索
解法一:假设满足条件的m存在,由A、B、C三点共线,即∥,
∴存在实数λ,使=λ,
i-2j=λ(i+mj),
∴m=-2
∴当m=-2时,A、B、C三点共线
解法二:假设满足条件的m存在,根据题意可知:i=(1,O),j=(O,1)
∴=(1,O)-2(O,1)=(1,-2),
=(1,O)+m(O,1)=(1,m),
由A、B、C三点共线,即∥,
故1·m-1·(-2)=O解得m=-2
∴当m=-2时,A、B、C三点共线
评述: (1)共线向量的充要条件有两种不同的表示形式,但其本质是一样的,在运用中各有特点,解题时可灵活选择
(2)本题是存在探索性问题,这类问题一般有两种思考方法,即假设存在法——当存在时;假设否定法——当不存在时
四、课堂练习:
1判断题
(1) +=O(√)(2)O=O(×)(3)-=(×)
2选择题
已知a,b为两个单位向量,下列四个命题中正确的是( )
A.a与b相等 B.如果a与b平行,那么a与b相等
Ca·b=1 D.a2=b2
答案:D
3已知A、B、C是直线l上的顺次三点,指出向量、、、中,哪些是方向相同的向量
答案:与方向相同,与方向相同
4已知为与的和向量,且=a,=b,分别用a、b表示,
解:=(a-b),=(a+b)
5已知ABCDEF为正六边形,且=a,=b,用a,b表示向量、、、、、、、
解:=-a,=a+b,=(a+b),=-(a+b),=(a-b),=(b-a),=a+b,=b-a
6已知点A(-3,-4)、B(5,-12)
(1)求的坐标及||;
(2)若=+,=-,求及的坐标;
(3)求·
解:(1) =(8,-8),||=8
(2) =(2,-16),=(-8,8)
(3) ·=33
五、小结
通过本节学习,要求大家在了解向量知识网络结构基础上,进一步熟悉基本概念及运算律,并能熟练重要定理、公式的应用,并加强数学应用意识,提高分析问题、解决问题的能力
六、课后作业:
七、板书设计(略)
八、课后记及备用资料:
1三点共线的证明
对于三点共线的证明,可以利用向量共线的充要条件证明,也可利用定比分点知识证明因为,定比分点问题中所涉及的三个点必然共线,而三个点共线时,必然构成定比分点
例1已知A(-1,-1)、B(1,3)、C(2,5),求证A、B、C三点共线
证明:设点B′(1,y)是的一个分点,且=λ,则1=
解得λ=2
∴y==3
即点B′与点B重合
∵点B′在上,∴点B在上,
∴A、B、C三点共线
2利用正、余弦定理判断三角形形状
例2根据下列条件,判断△ABC的形状
(1)acosA=bcosB
(2)sin2Α+sin2B=sin2C,且c=2acosB
解:(1)∵acosA=bcosB∴∴
即sinAcosA=sinBcosB
∴sin2A=sin2B ∴2A=2B或2A=π-2B∴A=B或A+B=
∴△ABC是等腰三角形或直角三角形
(2)∵sin2A+sin2B=sin2C
∴ ∴a2+b2=c2
故△ABC是直角三角形,且C=9O°,
∴cosB=,代入c=2acosB得cosB= ∴B=45°,A=45°
综上,△ABC是等腰直角三角形
评注(1)条件中有边有角,一般须化边为角或化角为边,题(1)也可以化角为边
(2)题(1)结论中用“或”,题(2)中用“且”结论也就不同,切不可混淆
例3 在△ABC中,若a2=b(b+c),则A与B有何关系?
解:由正弦定理得sin2A=sinB(sinB+sinC)
∴sin2A-sin2B=sinB·sinC,
(sinA+sinB)(sinA-sinB)=sinBsinC,
sin(A+B)sin(A-B)=sinB·sinC
∵sin(A+B)=sinC,∴sin(A-B)=sinB,
∴A-B=B,A=2B,或A-B=π-B(舍去)
故A与B的关系是A=2B
3利用正、余弦定理证明三角恒等式
例4 在△ABC中,求证
证明:由余弦定理,知
a2+b2-c2=2abcosC,a2-b2+c2=2cacosB,
∴
评注:对于含有a2、b2、c2的形式,常用余弦定理化边为角
例5 在△ABC中,已知2sin2A=3sin2B+3sin2C ①
cos2A+3cosA+3cos(B-C)=1 ②求:a∶b∶c
解:由①得2a2=3b2+3c2 ③
∵cosA=-cos(B+C)
由②得3cos(B-C)-3cos(B+C)=1-cos2A=2sin2A=3sin2B+3sin2C
∴cos(B-C)-cos(B+C)=sin2B+sin2C,
2sinBsinC=sin2B+sin2C
即(sinB-sinC)2=O,∴sinB=sinC,
∴2RsinB=2RsinC,∴b=c代入③得a=b
∴a∶b∶c=b∶b∶b=∶1∶1
相关文档
- 高中数学必修1教案:第五章(第13课时)2021-06-18 01:12:435页
- 高中数学必修1教案:第四章(第33课时)2021-06-18 00:01:418页
- 高中数学必修1教案:第四章(第24课时)2021-06-17 21:08:486页
- 高中数学必修1教案第一章 章末复习2021-06-17 20:20:076页
- 高中数学必修1教案:第四章(第29课时)2021-06-07 18:31:297页
- 高中数学必修1教案3_2_2-2自建函数2021-06-07 12:30:307页
- 高中数学必修1教案:第五章(第18课时)2021-06-07 12:13:517页
- 高中数学必修1教案:第九章直线平面2021-06-04 16:21:046页
- 高中数学必修4同步练习:向量在物理2021-06-03 22:07:215页
- 高中数学必修1教案:第一章(第8课时)2021-06-03 20:53:424页