人教版八年级数学下册-第十八章检测题 6页

第十八章检测题 (时间：120 分钟满分：120 分) 一、选择题(每小题 3 分，共 30 分) 1．(2019·十堰)矩形具有而平行四边形不一定具有的性质是 C A．对边相等 B．对角相等 C．对角线相等 D．对角线互相平分 2．(株洲中考)如图，已知四边形 ABCD 是平行四边形，对角线 AC，BD 相交于点 O，E 是 BC 的中点，以下说法错误的是 D A．OE＝1 2DCB．OA＝OCC．∠BOE＝∠OBAD．∠OBE＝∠OCE 第 2 题图 第 3 题图 第 6 题图 3．如图，矩形 ABCD 的对角线 AC＝8cm，∠AOD＝120°，则 AB 的长为 D A． 3cmB．2cmC．2 3cmD．4cm 4．(2019·泸州)四边形 ABCD 的对角线 AC 与 BD 相交于点 O，下列四组条件中，一定 能判定四边形 ABCD 为平行四边形的是 B A．AD∥BCB．OA＝OC，OB＝ODC．AD∥BC，AB＝DCD．AC⊥BD 5．若顺次连接四边形各边中点所得的四边形是菱形，则该四边形一定是 C A．矩形 B．一组对边相等，另一组对边平行的四边形 C．对角线相等的四边形 D．对角线互相垂直的四边形 6．(2019·赤峰)如图，菱形 ABCD 周长为 20，对角线 AC，BD 相交于点 O，E 是 CD 的 中点，则 OE 的长是 A A．2.5B．3C．4D．5 7．(2019·泸州)一个菱形的边长为 6，面积为 28，则该菱形的两条对角线的长度之和为 C A．8B．12C．16D．32 8．如图，把矩形 ABCD 沿 EF 翻折，点 B 恰好落在 AD 边的 B′处，若 AE＝2，DE＝6， ∠EFB′＝60°，则矩形 ABCD 的面积是 D A．12B．24C．12 3D．16 3 第 8 题图 第 9 题图 第 10 题图 9．如图，正方形 ABCD 的边长为 4，点 E 在对角线 BD 上，且∠BAE＝22.5°，EF⊥ AB，垂足为 F，则 EF 的长为 C A．1B． 2C．4－2 2D．3 2－4 10．如图，在矩形 ABCD 中，点 E 是 AD 的中点，∠EBC 的平分线交 CD 于点 F，将 △DEF 沿 EF 折叠，点 D 恰好落在 BE 上点 M 处，延长 BC，EF 交于点 N，有下列四个结 论：①DF＝CF；②BF⊥EN；③△BEN 是等边三角形；④S△BEF＝3S△DEF，其中正确的结论 是 B A．①②③B．①②④C．②③④D．①②③④ 二、填空题(每小题 3 分，共 15 分) 11．(2019·长沙)如图，要测量池塘两岸相对的 A，B 两点间的距离，可以在池塘外选一 点 C，连接 AC，BC，分别取 AC，BC 的中点 D，E，测得 DE＝50m，则 AB 的长是 100m. 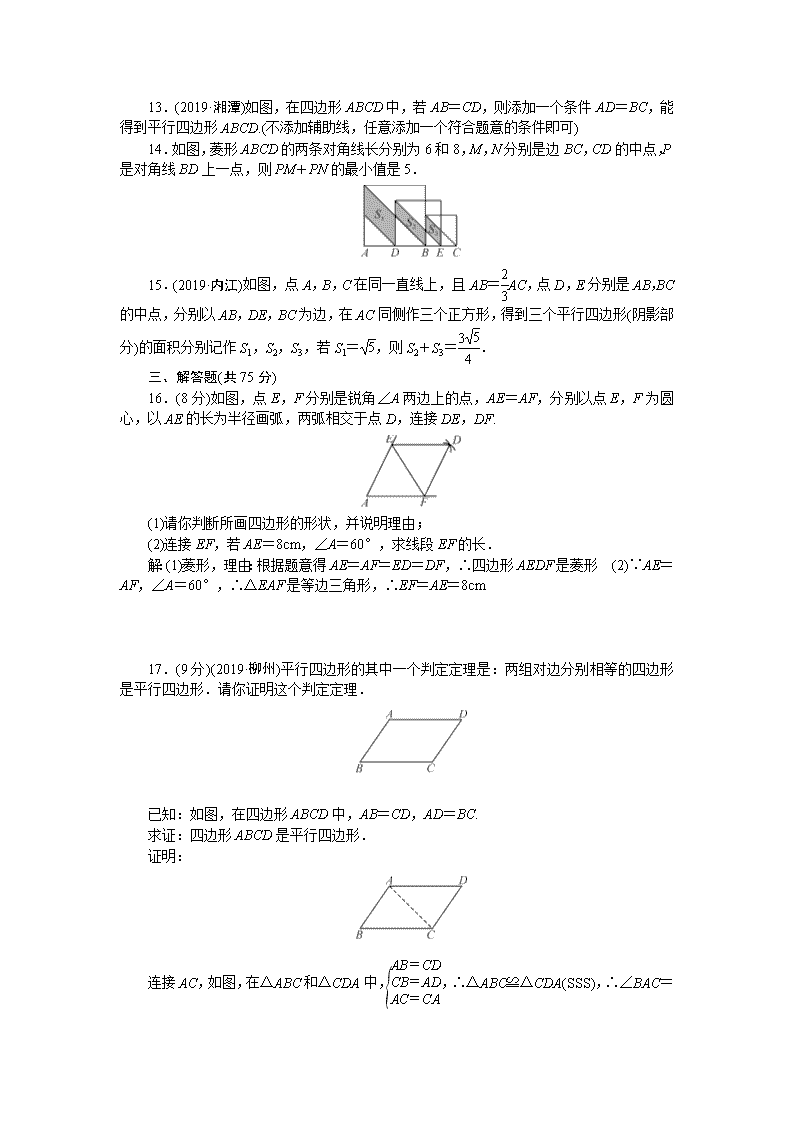第 11 题图 第 12 题图 第 13 题图 第 14 题图 12．(江西中考)如图，在▱ABCD 中，∠C＝40°，过点 D 作 CB 的垂线，交 AB 于点 E， 交 CB 的延长线于点 F，则∠BEF 的度数为 50°． 13．(2019·湘潭)如图，在四边形 ABCD 中，若 AB＝CD，则添加一个条件 AD＝BC，能 得到平行四边形 ABCD.(不添加辅助线，任意添加一个符合题意的条件即可) 14．如图，菱形 ABCD 的两条对角线长分别为 6 和 8，M，N 分别是边 BC，CD 的中点， P 是对角线 BD 上一点，则 PM＋PN 的最小值是 5． 15．(2019·内江)如图，点 A，B，C 在同一直线上，且 AB＝2 3AC，点 D，E 分别是 AB， BC 的中点，分别以 AB，DE，BC 为边，在 AC 同侧作三个正方形，得到三个平行四边形(阴 影部分)的面积分别记作 S1，S2，S3，若 S1＝ 5，则 S2＋S3＝3 5 4 ． 三、解答题(共 75 分) 16．(8 分)如图，点 E，F 分别是锐角∠A 两边上的点，AE＝AF，分别以点 E，F 为圆 心，以 AE 的长为半径画弧，两弧相交于点 D，连接 DE，DF. (1)请你判断所画四边形的形状，并说明理由； (2)连接 EF，若 AE＝8cm，∠A＝60°，求线段 EF 的长． 解：(1)菱形，理由：根据题意得 AE＝AF＝ED＝DF，∴四边形 AEDF 是菱形 (2)∵AE ＝AF，∠A＝60°，∴△EAF 是等边三角形，∴EF＝AE＝8cm 17．(9 分)(2019·柳州)平行四边形的其中一个判定定理是：两组对边分别相等的四边形 是平行四边形．请你证明这个判定定理． 已知：如图，在四边形 ABCD 中，AB＝CD，AD＝BC. 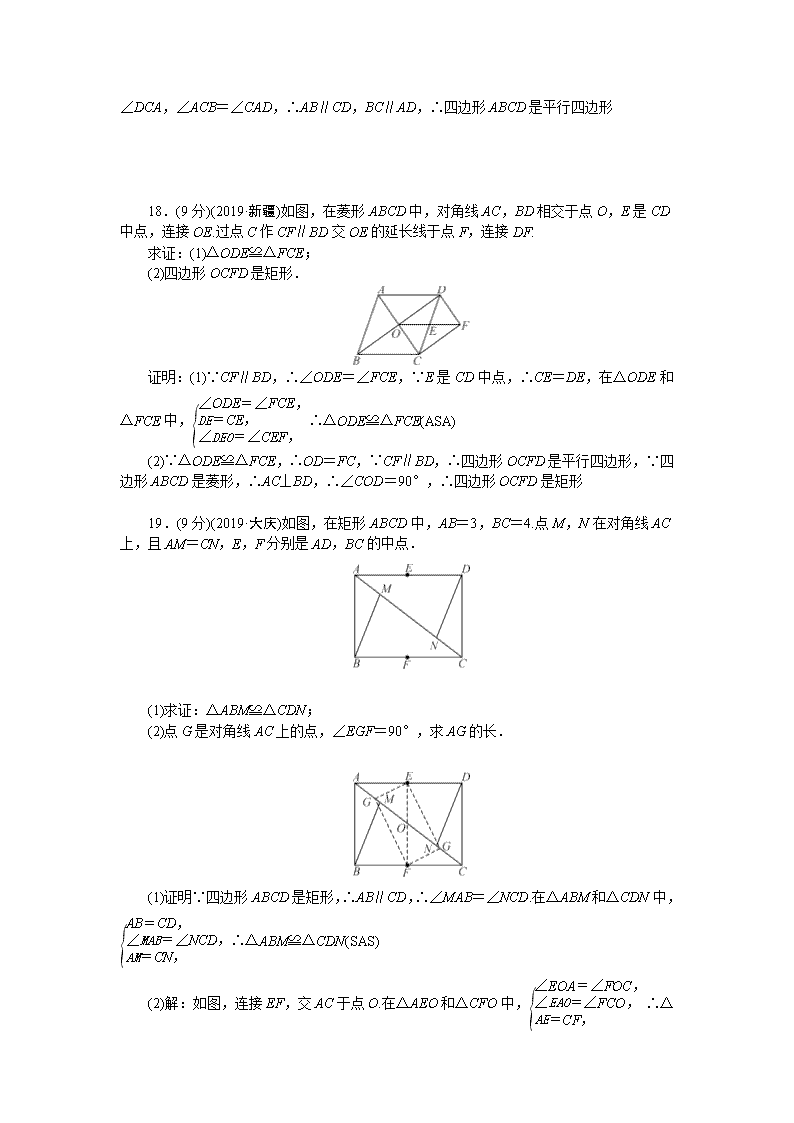求证：四边形 ABCD 是平行四边形． 证明： 连接 AC，如图，在△ABC 和△CDA 中， AB＝CD CB＝AD AC＝CA ，∴△ABC≌△CDA(SSS)，∴∠BAC ＝∠DCA，∠ACB＝∠CAD，∴AB∥CD，BC∥AD，∴四边形 ABCD 是平行四边形 18．(9 分)(2019·新疆)如图，在菱形 ABCD 中，对角线 AC，BD 相交于点 O，E 是 CD 中点，连接 OE.过点 C 作 CF∥BD 交 OE 的延长线于点 F，连接 DF. 求证：(1)△ODE≌△FCE； (2)四边形 OCFD 是矩形． 证明：(1)∵CF∥BD，∴∠ODE＝∠FCE，∵E 是 CD 中点，∴CE＝DE，在△ODE 和 △FCE 中， ∠ODE＝∠FCE， DE＝CE， ∠DEO＝∠CEF， ∴△ODE≌△FCE(ASA) (2)∵△ODE≌△FCE，∴OD＝FC，∵CF∥BD，∴四边形 OCFD 是平行四边形，∵四 边形 ABCD 是菱形，∴AC⊥BD，∴∠COD＝90°，∴四边形 OCFD 是矩形 19．(9 分)(2019·大庆)如图，在矩形 ABCD 中，AB＝3，BC＝4.点 M，N 在对角线 AC 上，且 AM＝CN，E，F 分别是 AD，BC 的中点． (1)求证：△ABM≌△CDN； (2)点 G 是对角线 AC 上的点，∠EGF＝90°，求 AG 的长． (1)证明∵四边形 ABCD 是矩形，∴AB∥CD，∴∠MAB＝∠NCD.在△ABM 和△CDN 中， AB＝CD， ∠MAB＝∠NCD， AM＝CN， ∴△ABM≌△CDN(SAS) (2)解：如图，连接 EF，交 AC 于点 O.在△AEO 和△CFO 中， ∠EOA＝∠FOC， ∠EAO＝∠FCO， AE＝CF， ∴△ AEO≌△CFO(AAS)，∴EO＝FO，AO＝CO，∴O 为 EF，AC 中点．∵∠EGF＝90°，OG ＝1 2EF＝3 2 ，∴AG＝OA－OG＝1 或 AG＝OA＋OG＝4，∴AG 的长为 1 或 4 20．(9 分)如图，在▱ABCD 中，E，F 两点在对角线 BD 上，BE＝DF. (1)求证：AE＝CF； (2)当四边形 AECF 为矩形时，请求出BD－AC BE 的值． 解：(1)由 SAS 证△ABE≌△CDF 即可 (2)连接 CE，AF，AC.∵四边形 AECF 是矩形， ∴AC＝EF，∴BD－AC BE ＝BD－EF BE ＝BE＋DF BE ＝2BE BE ＝2 21．(10 分)如图，在矩形 ABCD 中，M，N 分别是边 AD，BC 的中点，E，F 分别是线 段 BM，CM 的中点． (1)求证：△ABM≌△DCM； (2)填空：当 AB∶AD＝1∶2 时，四边形 MENF 是正方形，并说明理由． 解：(1)由 SAS 可证 (2)理由：∵AB∶AD＝1∶2，∴AB＝1 2AD，∵AM＝1 2AD，∴AB＝ AM，∴∠ABM＝∠AMB，∵∠A＝90°，∴∠AMB＝45°，∵△ABM≌△DCM，∴BM＝ CM，∠DMC＝∠AMB＝45°，∴∠BMC＝90°，∵E，F，N 分别是 BM，CM，BC 的中点， ∴EN∥CM，FN∥BM，EM＝MF，∴四边形 MENF 是菱形，∵∠BMC＝90°，∴菱形 MENF 是正方形 22．(10 分)如图，在正方形 ABCD 中，AC 是对角线，今有较大的直角三角板，一边始 终经过点 B，直角顶点 P 在射线 AC 上移动，另一边交 DC 于点 Q. (1)如图①，当点 Q 在 DC 边上时，猜想并写出 PB 与 PQ 所满足的数量关系，并加以证 明； (2)如图②，当点 Q 落在 DC 的延长线上时，猜想并写出 PB 与 PQ 满足的数量关系，并 证明你的猜想． 解：(1)PB＝PQ.证明：连接 PD，∵四边形 ABCD 是正方形，∴∠ACB＝∠ACD，∠BCD ＝90°，BC＝CD，又∵PC＝PC，∴△DCP≌△BCP(SAS)，∴PD＝PB，∠PBC＝∠PDC， ∵∠PBC＋∠PQC＝180°，∠PQD＋∠PQC＝180°，∴∠PBC＝∠PQD，∴∠PDC＝ ∠PQD，∴PQ＝PD，∴PB＝PQ (2)PB＝PQ.证明：连接 PD，同(1)可证△DCP≌△BCP， ∴PD＝PB，∠PBC＝∠PDC，∵∠PBC＝∠Q，∴∠PDC＝∠Q，∴PD＝PQ，∴PB＝PQ 23．(11 分)(2019·重庆)如图，在平行四边形 ABCD 中，点 E 在边 BC 上，连接 AE，EM ⊥AE，垂足为 E，交 CD 于点 M，AF⊥BC，垂足为 F，BH⊥AE，垂足为 H，交 AF 于点 N， 点 P 是 AD 上一点，连接 CP. (1)若 DP＝2AP＝4，CP＝ 17，CD＝5，求△ACD 的面积． (2)若 AE＝BN，AN＝CE，求证：AD＝ 2CM＋2CE. 解：(1)作 CG⊥AD 于 G，如图①所示：设 PG＝x，则 DG＝4－x，在 Rt△PGC 中，GC2 ＝CP2－PG2＝17－x2，在 Rt△DGC 中，GC2＝CD2－GD2＝52－(4－x)2＝9＋8x－x2，∴17－ x2＝9＋8x－x2，解得：x＝1，即 PG＝1，∴GC＝4，∵DP＝2AP＝4，∴AD＝6，∴S△ACD＝ 1 2 ×AD×CG＝1 2 ×6×4＝12 (2)证明：连接 NE，如图②所示：∵BH⊥AE，AF⊥BC，AE⊥EM，∴∠AEB＋∠NBF ＝∠AEB＋∠EAF＝∠AEB＋∠MEC＝90°，∴∠NBF＝∠EAF＝∠MEC，在△NBF 和△EAF 中， ∠NBF＝∠EAF， ∠BFN＝∠AFE， BN＝AE， ∴△NBF≌△EAF(AAS)，∴BF＝AF，NF＝EF，∴∠ABC＝45°， ∠ENF＝45°，∵∠ANB＝90°＋∠EAF，∠CEA＝90°＋∠MEC，∴∠ANB＝∠CEA，在 △ANB 和△CEA 中， AN＝CE， ∠ANB＝∠CEA， BN＝AE， ∴△ANB≌△CEA(SAS)，∴∠CAE＝∠ABN，∵∠ NBF＝∠EAF，∴∠ABF＝∠FAC＝45°∴FC＝AF＝BF，∴∠ANE＝∠BCD＝135°，AD＝ BC＝2AF，在△ANE 和△ECM 中， ∠EAF＝∠MEC， AN＝EC， ∠ANE＝∠ECM， ∴△ANE≌△ECM(ASA)，∴CM＝ NE，又∵NF＝ 2 2 NE＝ 2 2 MC，∴AF＝ 2 2 MC＋EC，∴AD＝ 2MC＋2EC