- 765.50 KB
- 2021-05-23 发布
回顾:
1.
向量共线定理:
2.
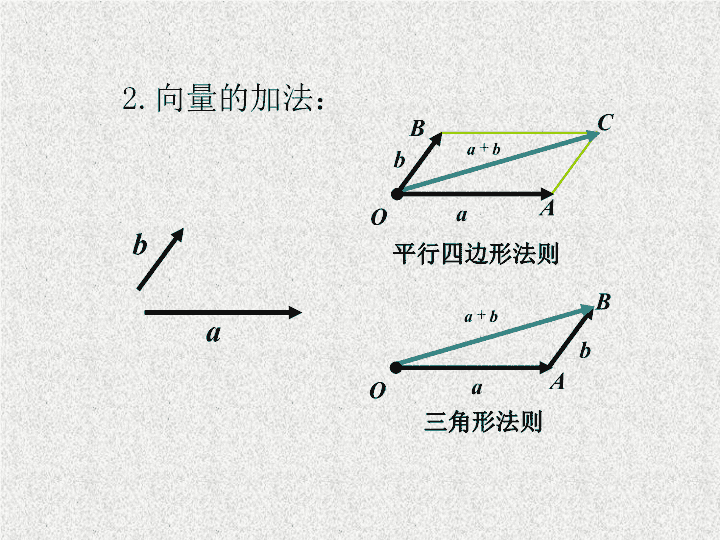
向量的加法:
O
B
C
A
平行四边形法则
O
A
B
三角形法则
如下图,由向量的运算性质可知,存在实数
使得
,
由于
所以
.
平面向量基本定理:
如果
是同一平面内的两个不共线向量,
那么对于这一平面内的任意向量
,
有且只有
一对实数
,使
我们把不共线的向量
叫做表示这一平面
内所有向量的一组
基底
.
特别的,若
,则有且只有
,
使得
若
与
共线,则
使得
向量的夹角
:
已知两个非零向量
,作
,则
叫做向量
与
的
夹角
.
当
时,
与
同向;当
时,
与
反向;当
时,
与
垂直,记
作
.
解:以
为邻边作平行四边形
,
如图所示:
,而
是平行四边形
对角线
的中点,所以
也是
的中点
.
所以
课堂练习:
D