- 415.99 KB
- 2021-05-23 发布
学习目标
1、了解等腰三角形的有关概念。
2、掌握识别等腰三角形的两种方
法。
3、掌握并能熟练应用等腰三角形
的性质定理和三线合一性质解决有
关问题。
4、通过习题,能总结代数法求几
何角的大小、线段长度的方法。
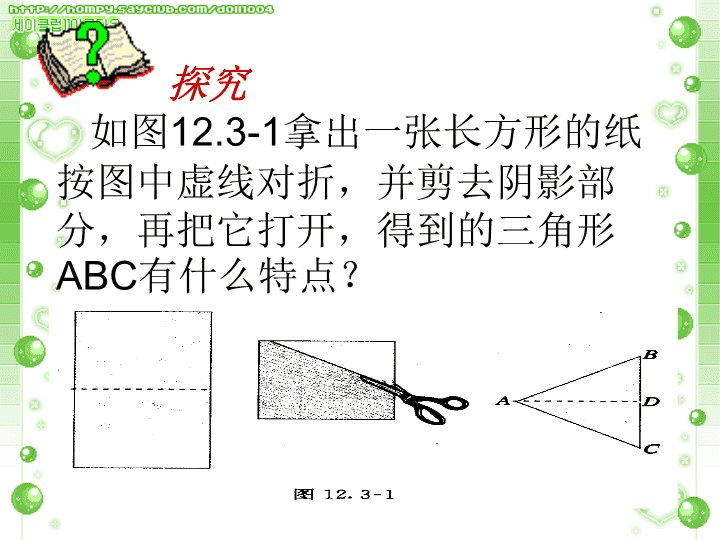
探究
如图12.3-1拿出一张长方形的纸
按图中虚线对折,并剪去阴影部
分,再把它打开,得到的三角形
ABC有什么特点?
定义:我们知道两条边相等的三角形叫
做等腰三角形(isosceles triangle).如图
所示,AB=AC,△ABC就是等腰三角形.
等腰三角形中,
相等的两边都叫腰,
另一边叫做底边,
两腰的夹角叫做角,
腰和底边的夹角叫底角.
想一想
1、上面剪出的等腰三角形是轴对称图形吗?
2、把剪出的等腰三角形ABC沿折痕对折,找出
其中重合的线段和角。
3、由这些重合的线段和角,你能发现等腰三角
形的哪些性质呢?说一说你的猜想。
我们可以发现等腰三角形的性质
性质1:等腰三角形的两个底角相等(简写为
“等边对等角”)
性质2:等腰三角形的顶角平分线、底边上的中
线、底边上的高线相互重合(简称为“三线合
一”)
证明性质1:等腰三角形的两个底角相
等
已知: △ ABC中, AB=AC.
求证: ∠B= ∠C.
A
B C
21
作顶角的平分线
证明:作顶角的平分线AD.
在△BAD和△CAD中,
AB=AC ( 已知 ),
∠ 1= ∠ 2 ( 辅助线作法 ),
AD=AD (公共边) ,
∴ △BAD ≌ △CAD (SAS).
∴ ∠B= ∠C.
想一想,做一
做:我们如何
证明性质2呢?
如图在△ABC中,AB=AC,点D在
AC上,且 BD=BC=AD求△ABC各
角的度数.
解:∵AB=AC, BD=BC=AD
∴∠ABC=∠C=∠BDC
∠A=∠ABD
设∠A=x,则 ∠BDC=∠A+∠ABD=2x°
从而∠ABC=∠C=∠BDC=2x°
于是在△ABC中,有
∠A+∠ABC+∠C=x+2x+2x=180
解得x=36
在△ABC中,∠A=36°,
∠ABC=∠C=72°.
1 、在等腰△ABC中,AB =AC, ∠A = 36°,则∠B
=——,∠C=——
2、在等△ABC腰中,AB=AC,∠A = 50°, 则∠B
=——,∠C=——
3、在等△ABC腰中,AB=AC,∠A = 120°则
∠B =——,∠C=——
72° 72°
65°65°
30° 30°
v1、△ ABC是等腰直角三角形(AB=AC,∠BAC=90°),
AD是底边BC上的高,标出∠ B, ∠ C, ∠ BAD, ∠ DAC
的度数,图中有哪些相等的线段?
B
A
C
D
v2、在△ ABC中,AB=AD=DC, ∠BAD=26°,求∠ B
和∠ C的度数
B D C
A
这节课我们学习了什么?
1、求有关等腰三角形的问题,作
顶角平分线、底边中线,底边的
高是常用的辅助线;
2、熟练掌握求解等腰三角形的顶
角、底角的度数;
3、掌握等腰三角形三线合一的
应用。
相关文档
- 八年级下数学课件:17-2 勾股定理的2021-05-23 01:09:1322页
- 八年级下数学课件《平行四边形》课2021-05-23 00:32:4424页
- 八年级下数学课件八年级下册数学课2021-05-23 00:11:2013页
- 八年级下数学课件:18-1-2 平行四边2021-05-22 23:03:1928页
- 八年级下数学课件《二次根式》课件2021-05-22 22:53:3724页
- 八年级下数学课件:18-1-1 平行四边2021-05-22 22:49:0016页
- 八年级下数学课件《分式的加减》课2021-05-22 21:59:1921页
- 八年级下数学课件八年级下册数学课2021-05-22 21:48:5611页
- 八年级下数学课件3-3 轴对称和平移2021-05-22 21:43:1814页
- 八年级下数学课件《数据的整理与表2021-05-22 21:42:3919页