- 811.50 KB
- 2021-05-23 发布
湖北省竹溪一中、竹山一中、房县一中三校2019-2020学年
高二下学期7月联考试题
一、选择题(本大题共12小题,共60分)
1.已知集合A=,B=,则A∩B中元素的个数为( )
A.3 B.2 C.1 D.0
2. 若,则( )
A. B. C. D.
3. 若,则( )
A. B. C. D.
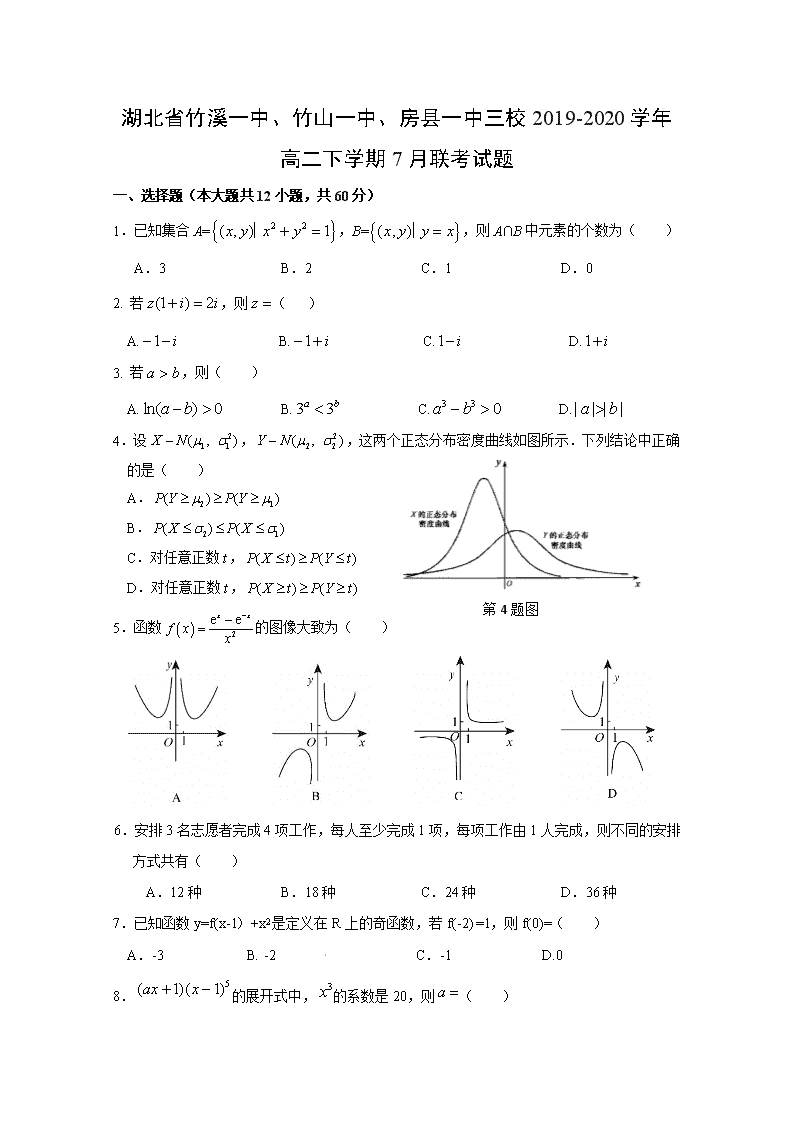
4.设,,这两个正态分布密度曲线如图所示.下列结论中正确的是( )
A.
B.
C.对任意正数,
第4题图
D.对任意正数,
5.函数的图像大致为( )
6.安排3名志愿者完成4项工作,每人至少完成1项,每项工作由1人完成,则不同的安排方式共有( )
A.12种 B.18种 C.24种 D.36种
7.已知函数y=f(x-1)+x2是定义在R上的奇函数,若f(-2) =1,则f(0)=( )
A.-3 B. -2 C.-1 D.0
8.的展开式中,的系数是20,则( )
A.2 B.-1 C.4 D.1
9.等差数列的首项为1,公差不为0.若a2,a3,a6成等比数列,则前6项的和为( )
A.-24 B.-3 C.3 D.8
10.已知F为抛物线C:y2=4x的焦点,过F作两条互相垂直的直线l1,l2,直线l1与C交于A、B两点,直线l2与C交于D、E两点,则|AB|+|DE|的最小值为( )
A.16 B.14 C.12 D.10
11.若在是减函数,则的最大值是( )
A. B. C. D.
12.设函数=,其中a1,若存在唯一的整数,使得0,则的取值范围是( )
A.[-,1) B.[-,) C.[,) D.[,1)
二、填空题(本大题共4小题,共20分)
13.曲线在点处的切线的斜率为,则 .
14.记为数列的前项和.若,则 .
15. 从1,2,3,4,5中任取2个不同的数,事件A=“取到的2个数之和为偶数”,事件B=“取到的2个数均为偶数”,则P(B|A)= .
16.已知双曲线C:(a>0,b>0)的右顶点为A,以A为圆心,b为半径做圆A,圆A与双曲线C的一条渐近线交于M、N两点。若∠MAN=60°,则C的离心率为________.
三、解答题(本大题共6小题,共70分)
17.(10分)的内角的对边分别为,已知.
(1)求;
(2)若,的面积为,求.
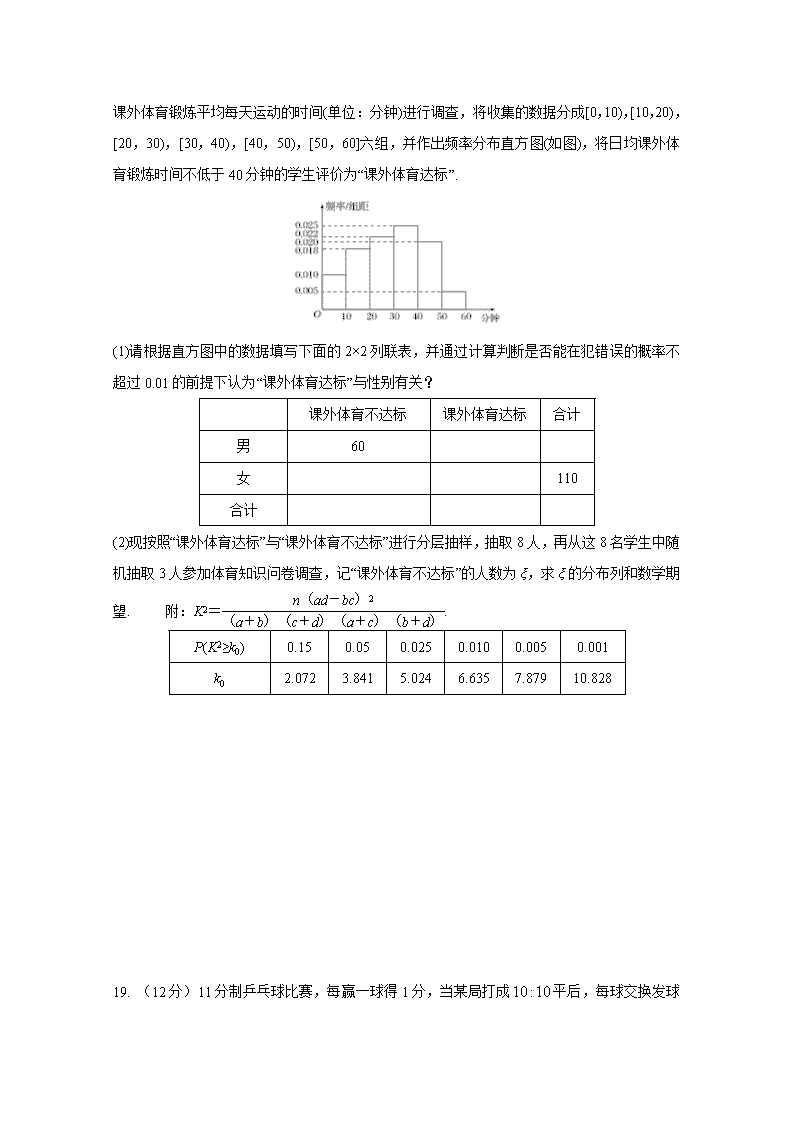
18.(12分)某中学为研究学生的身体素质与课外体育锻炼时间的关系,对该校200名学生的课外体育锻炼平均每天运动的时间(单位:分钟)进行调查,将收集的数据分成[0,10),[10,20),[20,30),[30,40),[40,50),[50,60]六组,并作出频率分布直方图(如图),将日均课外体育锻炼时间不低于40分钟的学生评价为“课外体育达标”.
(1)请根据直方图中的数据填写下面的2×2列联表,并通过计算判断是否能在犯错误的概率不超过0.01的前提下认为“课外体育达标”与性别有关?
课外体育不达标
课外体育达标
合计
男
60
女
110
合计
(2)现按照“课外体育达标”与“课外体育不达标”进行分层抽样,抽取8人,再从这8名学生中随机抽取3人参加体育知识问卷调查,记“课外体育不达标”的人数为ξ,求ξ的分布列和数学期望. 附:K2=.
P(K2≥k0)
0.15
0.05
0.025
0.010
0.005
0.001
k0
2.072
3.841
5.024
6.635
7.879
10.828
19. (12分)11分制乒乓球比赛,每赢一球得1分,当某局打成
平后,每球交换发球权,先多得2分的一方获胜,该局比赛结束.甲、乙两位同学进行单打比赛,假设甲发球时甲得分的概率为,乙发球时甲得分的概率为,各球的结果相互独立.在某局双方平后,甲先发球,两人又打了个球该局比赛结束.
(1) 求;
(2) 求事件“且甲获胜”的概率.
20.(12分)如图,四面体ABCD中,△ABC是正三角形,△ACD是直角三角形,
∠ABD=∠CBD,AB=BD.
(1)证明:平面ACD⊥平面ABC;
(2)过AC的平面交BD于点E,若平面AEC把四面体ABCD分成体积相等的两部分,求二面角D–AE–C的余弦值.
21.(12分)设椭圆的右焦点为,过的直线与交于,两点,点的坐标为.
⑴当与轴垂直时,求直线的方程;
⑵设为坐标原点,证明:.
22.(12分)已知函数.
(1) 讨论的单调性;
(2) 是否存在,使得在区间的最小值为且最大值为?若存在,求出的所有值;若不存在,说明理由.
参考答案
1
2
3
4
5
6
7
8
9
10
11
12
B
D
C
C
B
B
C
B
A
A
A
D
13. -3 14.-63 15. 0.25 16.
17.【解析】:(1)由题设及,故
上式两边平方,整理得 …………4
解得 …………5
(2)由,故
又 ……………7
由余弦定理及得
所以b=2 ……………10
18.【解析】(1)由题意得“课外体育达标”人数为200×[(0.02+0.005)×10]=50,
则“课外体育不达标”人数为150,
∴列联表如下:……………4
课外体育不达标
课外体育达标
合计
男
60
30
90
女
90
20
110
合计
150
50
200
∴K2==≈6.061<6.635 …………6
∴在犯错误的概率不超过0.01的前提下不能认为“课外体育达标”与性别有关.
(2)由题意采用分层抽样在“课外体育达标”的学生中抽取2人,在“课外体育不达标”的学生中抽取6人,由题意知:ξ的所有可能取值为1,2,3,
P(ξ=1)===;
P(ξ=2)===;
P(ξ=3)===;
故ξ的分布列为 …………10
ξ
1
2
3
P
故ξ的数学期望为E(ξ)=1×+2×+3×= ………12
19.【解析】(1)时,有两种可能:
①甲连赢两局结束比赛,此时; …………3
②乙连赢两局结束比赛,此时,…………5
∴; ……………6
(2) 且甲获胜,即平后,两人又打了4个球该局比赛结束,
且这4个球的得分情况为:前两球是甲、乙各得1分,后两球均为甲得分.
因此所求概率为. ………12
20.【解析】(1)由题设可得,
又是直角三角形,所以
取AC的中点O,连接DO,BO,则DO⊥AC,DO=AO
又由于
所以
.……………5
(2)由题设及(1)知,两两垂直,以为坐标原点,的方向为轴正方向,为单位长,建立如图所示的空间直角坐标系,则
…………6
由题设知,四面体ABCE的体积为四面体ABCD的体积的,从而E到平面ABC的距离为D到平面ABC的距离的,即E为DB的中点,得E.故
设是平面DAE的法向量,则
可取 …………9
设是平面AEC的法向量,则同理可得
则
所以二面角D-AE-C的余弦值为 ………12
21.【解析】(1)如图所示,将代入椭圆方程得,得,∴,∴,∴直线的方程为:.
…………………4
(2) 证明:当斜率不存在时,由(1)可知,结论成立;当斜率存在时,设其方程为,,联立椭圆方程有
即,…………………6
∴ ………………7
…………………8
(2) ,
(3) ∴,∴ ………………12
22.【解析】(1)
当时,,此时在单调递增.
当时,令,解得或,令,解得.
此时在单调递增,在单调递减.
当时,令,解得或,令,解得.
此时在单调递增,在单调递减.
综上可得,当时,在单调递增.
当时,在单调递增,在单调递减.
当时,在单调递增,在单调递减.…………6
由(1)中结论可知,当时,在单调递增,
此时,∴,满足题意.
当时,若,即,则在单调递减,
此时,∴,满足题意.
若,即,则在单调递减,在单调递增.
此时
∵
∴当时,,
由可得,与矛盾,故不成立.
当时,,
由可得,与矛盾,故不成立.
综上可知,或满足题意. ………………12