- 1.99 MB
- 2021-05-23 发布
微专题 74 利用几何关系求解最值问题
一、基础知识:
1、利用几何关系求最值的一般思路:
(1)抓住图形中的定点与定长,通常与求最值相关
(2)遇到线段和差的最值,经常在动点与定点共线的时候取到。因为当动点与定点不共线时,
便可围成三角形,从而由三角形性质可知两边之和大于第三边,两边之差小于第三边,无法
取得最值。所以只有共线时才有可能达到最值。要注意动点与定点相对位置关系。一般的,
寻找线段和的最小值,则动点应在定点连成的线段上;若寻找线段差的最小值,则动点应在
定点连成的线段延长线上。
(3)若所求线段无法找到最值关系,则可考虑利用几何关系进行线段转移,将其中某些线段
用其它线段进行表示,进而找到最值位置
(4)处理多个动点问题时,可考虑先只让一个动点运动,其他动点不动,观察此动点运动时
最值选取的规律,再根据规律让其他点动起来,寻找最值位置。
2、常见的线段转移:
(1)利用对称轴转移线段(详见例 1)
(2)在圆中,可利用与半径相关的直角三角形(例如半弦,圆心到弦的垂线,半径;或是切
线,半径,点与圆心的连线)通过勾股定理进行线段转移。
(3)在抛物线中,可利用“点到准线的距离等于该点到焦点的距离”的特点进行两个距离的
相互转化。
(4)在椭圆中,利用两条焦半径的和为常数,可将一条焦半径转移至另一条焦半径
(5)在双曲线中,利用两条焦半径的差为常数,也可将一条焦半径转移至另一条焦半径(注
意点在双曲线的哪一支上)
3、与圆相关的最值问题:
(1)已知圆C 及圆外一定点 P ,设圆C 的半径为 r 则圆上点到 P 点
距离的最小值为 PM PC r ,最大值为 PN PC r (即连
结 PC 并延长, M 为 PC 与圆的交点, N 为 PC 延长线与圆的交点
(2)已知圆C 及圆内一定点 P ,则过 P 点的所有弦中最长的为直径,
最短的为与该直径垂直的弦 MN
解:,弦长的最大值为直径,而最小值考虑弦长公式为 2 22AB r d ,若 AB 最小,则 d
C
P
A
B
要取最大,在圆中 CP 为定值,在弦绕 P 旋转的过程中, d CP ,所以 d CP 时, AB
最小
(3)已知圆 C 和圆外的一条直线l ,则圆上点到直线距离的
最小值为 C lPM d r ,距离的最大值为 C lPN d r
(过圆心C 作l 的垂线,垂足为 P ,CP 与圆 C 交于 M ,其
反向延长线交圆C 于 N
(4)已知圆C 和圆外的一条直线l ,则过直线l 上的点作圆的
切线,切线长的最小值为 PM
解: 2 2PM CP r ,则若 PM 最小,则只需 CP 最小即可,
所以 P 点为过C 作l 垂线的垂足时, CP 最小
过 P 作圆的切线,则切线长 PM 最短
4、与圆锥曲线相关的最值关系:
(1)椭圆:设椭圆方程为
2 2
2 2 1 0x y a ba b
① 焦半径:焦半径的最大值为 a c ,最小值为 a c
② 焦点弦:焦点弦长的最小值称为通径,为
22b
a
,此时焦点弦与焦点所在的坐标轴垂直
(2)双曲线:设双曲线方程为
2 2
2 2 1 0, 0x y a ba b
① 焦半径:焦半径的最小值为 a c ,无最大值
② 焦点弦:焦点弦长的最小值称为通径,为
22b
a
,此时焦点弦与焦点所在的坐标轴垂直
(3)抛物线:设抛物线方程为 2 2y px
① 焦半径:由抛物线的焦半径公式可知:焦半径的最小值为原点到焦点的距离,即
2
p
② 焦点弦:当焦点弦与焦点所在坐标轴垂直时,弦长最小,为 2p
二、典型例题:
l
M
C
P
N
l
C
P
M
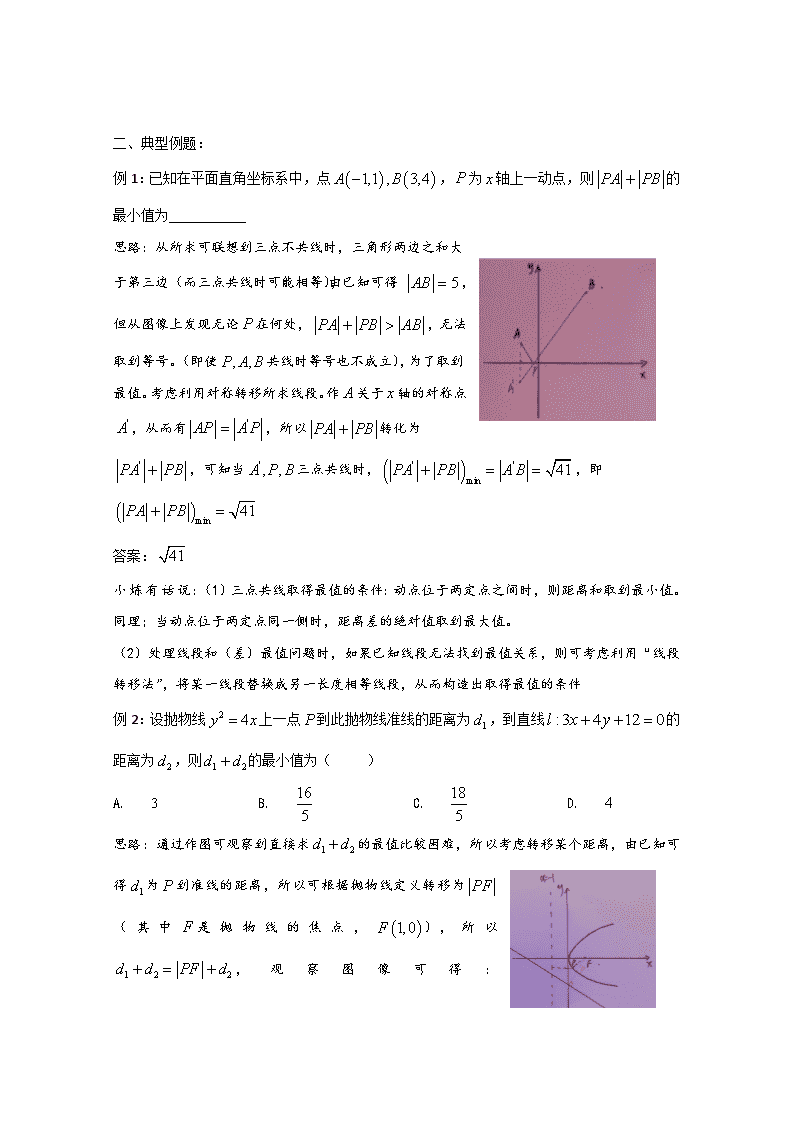
例 1:已知在平面直角坐标系中,点 1,1 , 3,4A B , P 为 x 轴上一动点,则 PA PB 的
最小值为___________
思路:从所求可联想到三点不共线时,三角形两边之和大
于第三边(而三点共线时可能相等),由已知可得:
5AB ,但从图像上发现无论 P 在何处,
PA PB AB ,无法取到等号。(即使 , ,P A B 共线时
等号也不成立),为了取到最值。考虑利用对称转移所求线
段。作 A 关于 x 轴的对称点 'A ,从而有 'AP A P ,所
以 PA PB 转化为 'PA PB ,可知当 ' , ,A P B 三点共线时,
' '
min
41PA PB A B ,即 min 41PA PB
答案: 41
小炼有话说:(1)三点共线取得最值的条件:动点位于两定点之间时,则距离和取到最小值。
同理;当动点位于两定点同一侧时,距离差的绝对值取到最大值。
(2)处理线段和(差)最值问题时,如果已知线段无法找到最值关系,则可考虑利用“线段
转移法”,将某一线段替换成另一长度相等线段,从而构造出取得最值的条件
例 2:设抛物线 2 4y x 上一点 P 到此抛物线准线的距离为 1d ,到直线 :3 4 12 0l x y 的
距离为 2d ,则 1 2d d 的最小值为( )
A. 3 B. 16
5
C. 18
5
D. 4
思路:通过作图可观察到直接求 1 2d d 的最值比较困难,所以考虑转移某个距离,由已知可
得 1d 为 P 到准线的距离,所以可根据抛物线定义转移为 PF
(其中 F 是抛物线的焦点, 1,0F ),所以 1 2 2d d PF d ,
观察图像可得: 2
3 1 12 35F lPF d d
答案:A
例 3:已知过抛物线 2 4y x 的焦点 F 的弦与抛物线交于 ,A B 两点,过 ,A B 分别作 y 轴的垂
线,垂足分别为 ,C D ,则 AC BD 的最小值为__________
思路:设抛物线的准线为l ,由抛物线 2 4y x 可知 : 1l x ,
观察图像可知 1, 1A l B lAC d BD d 。而由抛物线定义可
得 : ,A l B ld AF d BF , 所 以
1 1 2AC BD AF BF AB , 即 要 求 出
AC BD 的最小值,只需求出 AB 的最小值,即抛物线焦点弦
的最 小值 ,由抛 物线 性质可 知当 AB x 轴时 , AB 最小, min 2 4AB p ,所以
min 2AC BD
答案: 2
例 4:已知点 3, 12P
在抛物线 2: 2 0E x py p 的准线上,过点 P 作抛物线的切线,
若 切 点 A 在 第 一 象 限 , F 是 抛 物 线 的 焦 点 , 点 M 在 直 线 AF 上 , 点 N 在 圆
2 2: 2 2 1C x y 上,则 MN 的最小值为( )
A. 1
5
B. 6
5
C. 2 D. 6 2 1
思路:由图像可知,固定 M 点,则圆C 上到 M 距离的最小值 1CM r CM ,所以只
需在直线上找到与圆心C 距离最小的点,即C 到直线 AF 的
距离。需要确定抛物线方程和 A 点坐标,由 3, 12P
可得准
线 方 程 为 1y , 所 以 2p , 抛 物 线 方 程 为
2 214 4x y y x , 焦 点 0,1F 设 21, 4A a a
, 则
' 1
2y x , 切 线 斜 率 1
2k a , 从 而
21 1 14 43 2
2
a
k a a
a
, 即 4,4A ,
4 1 3
4 0 4AFk
,所以直线 AF 方程:3 4 4 0x y ,从而
min 22
6 8 4 11 53 4
MN
答案:A
例 5:抛物线 2y x 上的点到直线 4 3 8 0x y 距离的最小值是( )
A. 1
4
B. 4
3
C. 8
5
D. 3
思路一:直接利用点到直线距离公式得到距离关于 x 的函数,设抛物线上的点 2,P x x ,则
2
2
2 2034 3 8 3 3 20 1 4
5 5 3 5 3P l
xx x
d
,所以最小值为 4
3
思路二:本题也可将直线进行平移,平移至与抛物线相切,则两直线之间的距离即为所求最
小值。所以只需求与已知直线平行且与抛物线相切的直线,设切
点坐标为 0 0,x y ,所求函数的导数 ' 2y x ,因为切线与
4 3 8 0x y 平行,所以 0
42 3x ,可得 0
2
3x ,进而
2
0 0
4
9y x ,故切线方程为: 4 4 2
9 3 3y x
,整理后
可得: 44 3 03x y ,所以两直线距离
48 3 4
5 3d
,
即抛物线上的点到距离的最小值
答案:B
例 6 : 已 知 点 M 是 抛 物 线 2 4y x 的 一 点 , F 为 抛 物 线 的 焦 点 , A 在 圆
2 2: 4 1 1C x y 上,则 MA MF 的最小值为( )
A. 2 B. 3 C. 4 D. 5
思路:本题含两个动点 ,M A ,先固定一个点不动,寻找最小值的规律。考虑固定 M ,则圆
上距离 M 最近的点为 MC 与圆的交点,即 min 1MA MC r MC ,所以只需考虑
MC MF 的最小值即可,通过移动 M 可知,无论 M 位于何处, MC MF CF ,
所以 CF 不是最小值。考虑转移线段,抛物线的准线 : 1l x ,则 M lMF d ,所以
5M l C lMC MF MC d d ( 即 C 到 准 线 的 距 离 , 所 以
1 1 4C lMA MF MC MF d
答案:C
例 7:已知动点 ,P x y 在椭圆
2 2
125 16
x y 上,若点 A 的坐标
为 3,0 , 1, 0AM PM AM ,则 PM
的最小值是( )
A. 2 B. 3 C. 2 D. 3
思路:由椭圆方程可知 A 即为椭圆的焦点,由 1AM 可知 M 是以 A 为圆心,半径为 1 的
圆上的点,P 在圆外,且由 0PM AM 可得 PM AM ,所以 PM 即为圆上的切线,PM
的 最 小 值 即 切 线 长 的 最 小 值 , 由 圆 的 性 质 可 得 :
2 22 1PM PA r PA ,所以只需找到 PA 的最小
值即可,由椭圆性质可知: min 5 3 2PA a c ,故
2
min min 1 3PM PA
答案:B
例 8:设 1F 是椭圆
2 2
125 16
x y 的左焦点,P 是椭圆上的任意一点,
点 M 的坐标为 6,4 ,则 1PM PF 的最大值为___________
思路:先作出椭圆图像,标出定点 1,M F 的位置,若从 1F M 入手,
则由图发现无论 P 在何处, 1 1PM PF F M 。与所求最大值
不符。考虑进行线段转移,发现 1PF 为左焦半径,所以考虑作出右焦点 2 3,0F ,利用
1 2 2 10PF PF a 进 行 线 段 转 移 。 即 1 210PM PF PM PF , 只 需 求 出
2 maxPM PF , 结 合 图 像 可 得 2 2PM PF F M , 且
2 2
2 6 3 4 0 5F M ,从而可得: 1 2max 10 15PM PF F M
答案:15
例 9:设 P 是椭圆
2 2
19 5
x y 上一点, ,M N 分别是两圆 2 2
1 : 2 1C x y 和 2 :C
2 22 1x y 上的点,则 PM PN 的最小值和最大值分别为( )
A. 4,8 B. 2,6 C. 6,8 D. 8,12
思路:本题有三个动点 , ,P M N ,但观察可得 ,PM PN 之间没
有联系,所以若 PM PN 达到最小,则只需 ,PM PN 分别
达 到 最 小 即 可 。 固 定 P 点 , 可 知
1 1 1 2 2 2min min1, 1PM PC r PC PN PC r PC
,所以 1 2 2PM PN PC PC ,可知 1 22,0 , 2,0C C 恰好为椭圆两个定点,所
以由椭圆定义可得: 1 2 2 6PC PC a ,所以 min 6 2 4PM PN ,同理可知:
1 1 1 2 2 2max max1, 1PM PC r PC PN PC r PC , 所 以
max 6 2 8PM PN
答案:A
例 10 : 设 ,P Q 分 别 为 22: 6 2C x y 和 椭 圆
2
2 110
x y 上 的 点 , 则 ,P Q 两 点 间 的 最 大 距 离 是
___________
思路:本题中 ,P Q 均为动点,所以考虑先固定一点不动,
比如Q 点,寻找此时达到最值时 P 位置的规律,进而再让
Q 运动起来,找到最值。观察图像可得Q 点固定时, PQ 达到的最大值时 P 在QC 延长线与
C 的交点处,即 PQ QC r ,由于 2r ,所以只需找到 QC 的最大值即可,设
,Q x y ,而 0,6C ,则 2 22 6QC x y ,由
2
2 110
x y 可得 2 210 1x y ,代入
消去 x 可得:
2
2 22 2 210 1 6 9 12 46 9 503QC y y y y y
,因为
1,1y ,所以当 2
3y 时, 2
max 50 5 2QC QC ,从而 6 2PQ QC r
答案: 6 2
三、历年好题精选
1、(2014,安徽)在平面直角坐标系 xOy 中,已知向量 , , 1, 0a b a b a b ,点
Q 满足 2OQ a b ,曲线 | cos sin ,0 2C P OP a b ,区域
| 0 ,P r PQ R r R ,若C 为两段分离的曲线,则( )
A. 1 3r R B. 1 3r R C. 1 3r R D. 1 3r R
2、已知直线 1 : 4 3 6 0l x y 和直线 2 : 1l x ,则抛物线 2 4y x 上一动点 P 到直线 1 2,l l
的距离之和的最小值是( )
A. 2 B. 3 C. 11
5
D. 37
16
3、已知点 4,0A 和 2,2B , M 是椭圆
2 2
125 9
x y 上一动点,则 MA MB 的最
大值为_________
4、已知点 3, 12P
在抛物线 2: 2 0E x py p 的准线上,过点 P 作抛物线的切线,若切
点 A 在第一象限, F 是抛物线的焦点,点 M 在直线 AF 上,点 N 在圆
2 2: 2 2 1C x y 上,则 MN 的最小值为( )
A. 1
5
B. 6
5
C. 2 D. 6 2 1
5、已知圆 2 2
1 : 2 3 1C x y ,圆 2 2
2 : 3 4 9C x y , ,M N 分别是圆 1 2,C C
上的动点, P 为 x 轴上的动点,则 PM PN 的最小值为 ( )
A.5 2 4 B. 17 1 C. 6 2 2 D. 17
6、(2016,绵阳二模)已知点 P 在单位圆 122 yx 上运动,点 P 到直线3 4 10 0x y 与
3x 的距离分别记为 1 2,d d ,则 1 2d d 最小值为_________.
7、已知点 P 是双曲线
2 2
136 64
x y 的右支上一点, ,M N 分别是圆 2 210 4x y 和
2 210 1x y 上的点,则 PM PN 的最大值为_________
习题答案:
1、答案:A
解析:由 ,a b
的特点可以以 ,a b
所在直线为坐标轴建系,则有 1,0 , 0,1a b ,
所以曲线C 上点的坐标为 cos ,sin ,即圆心是原点的单位圆;另一方面
2, 2OQ 可得 2, 2 , 2Q OQ ,所以 区域为以Q 为圆心, ,r R 为半径的
圆环。通过数形结合可得若C 为两段分离的曲线,意味着以Q 为圆心, ,r R 为
半径的圆均与单位圆相交。所以
1
1 1 3
1
OQ r
R r R
OQ R
2、答案:A
解析:观察直线 2l 的方程恰好是抛物线的准线,所以想到 P 到 2l 的距离与 PF 相等( F 是抛
物线的焦点)。以此为突破口进行线段转移,所以
1 2 1P l P l P ld d d PF ,通过作图观察
可得
1 1P l F ld PF d (等号成立条件:P 为 F 到 1l 的垂线与抛物线的焦点),且 1,0F ,
所以 1 2 1min
4 0 6 25P l P l F ld d d
3、答案:10+2 10
解析:可知 A 是椭圆的右焦点,如图所示,设椭圆的左焦点
为 1 4,0A ,连接 1BA 并延长交椭圆于 1M ,则 1M 是使
MA MB 取得最大值的点.事实上,对于椭圆上的任意点
M 有: 2 2
1 12 2 2 5 6 2 10 2 10MA MB a MA MB a A B
4、答案:A
解析:由点 3, 12P
在抛物线准线上可得: 2p
2 21: 4 4E x y y x ' 1
2y x
设 21, 4A a a
2
'
1 1 14| 3 2
2
AP x a
a
k y a
a
解得: 4, 1a a (舍)
4,4A 由 0,1F 可得 AF 的方程为: 31 3 4 4 04y x x y
M 在直线 AF 上, N 在圆上
2 2
3 2 4 2 4 6 11 15 53 4C lMN d r
5、答案:A
解析:设圆 1 2,C C 的半径为 1 2,r r ,即 1
2
1
3
r
r
,可知 1 1 2 2,PM PC r PN PC r
1 2 1 2 1 2 4PM PN PC PC r r PC PC
1 2,3C 关于 x 轴对称点为 '
1 2, 3C
2 2' '
1 2 1 2 1 2 2 3 3 4 5 2PC PC PC PC C C
5 2 4PM PN ,等号成立条件: '
1 2, ,C C P 共线
6、答案: 4 55 5
解析:设点 cos ,sinP ,可得 1 2 2
3cos 4sin 10 10 4sin 3cos
53 4
d
,
2 3 cosd ,所以 1 2
1 4 55 4sin 8cos 5 sin5 5d d ,所以 1 2d d 的
最小值为 4 55 5
7、答案:15
解析:在双曲线
2 2
136 64
x y 中, 6, 8, 10a b c
1 210,0 , 10,0F F 1 2 2 12PF PF a
1 1 2 2,MP PF MF PN PF NF
1 1 2 2 15PM PN PF MF PF NF