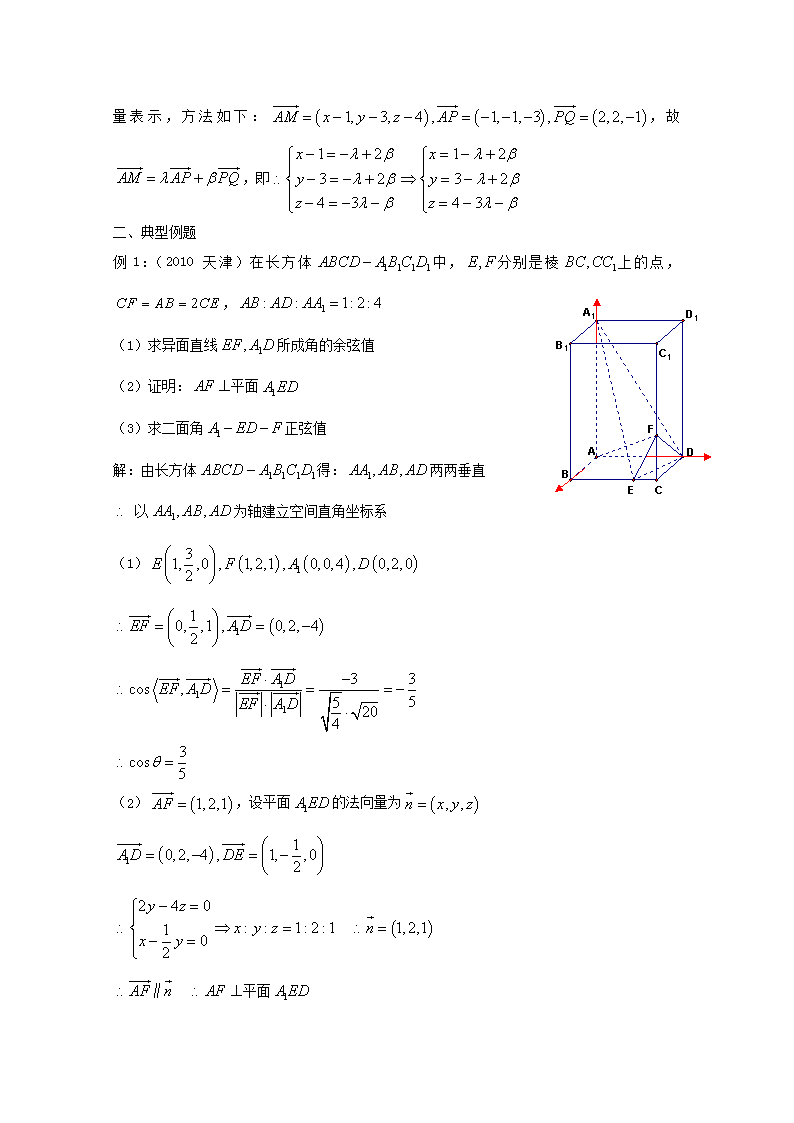【数学】2020届一轮复习人教B版空间向量解立体几何（含综合题习题）学案 25页

微专题64 利用空间向量解立体几何问题 一、基础知识 ‎（一）刻画直线与平面方向的向量 ‎1、直线：用直线的方向向量刻画直线的方向问题，而方向向量可由直线上的两个点来确定 例如：，则直线的方向向量为 ‎ ‎2、平面：用平面的法向量来刻画平面的倾斜程度，何为法向量？与平面垂直的直线称为平面的法线，法线的方向向量就是平面的法向量，如何求出指定平面的法向量呢？‎ ‎（1）所需条件：平面上的两条不平行的直线 ‎（2）求法：（先设再求）设平面的法向量为，若平面上所选两条直线的方向向量分别为，则可列出方程组：‎ ‎ 解出的比值即可 例如：，求所在平面的法向量 解：设，则有 ，解得： ‎ ‎ ‎ ‎（二）空间向量可解决的立体几何问题（用表示直线的方向向量，用表示平面的法向量）‎ ‎1、判定类 ‎（1）线面平行： ‎ ‎（2）线面垂直：‎ ‎（3）面面平行：‎ ‎（4）面面垂直：‎ ‎2、计算类：‎ ‎（1）两直线所成角： ‎ ‎（2）线面角：‎ ‎（3）二面角：或（视平面角与法向量夹角关系而定）‎ ‎（4）点到平面距离：设为平面外一点，为平面上任意一点，则到平面的距离为，即在法向量上投影的绝对值。‎ ‎（三）点的存在性问题：在立体几何解答题中，最后一问往往涉及点的存在性问题，即是否在某条线上存在一点，使之满足某个条件，本讲主要介绍使用空间向量解决该问题时的方法与技巧 ‎1、理念：先设再求——先设出所求点的坐标，再想办法利用条件求出坐标 ‎2、解题关键：减少变量数量——可表示空间中的任一点，但题目中所求点往往是确定在某条线或者某个平面上的，所以使用三个变量比较“浪费”（变量多，条件少，无法求解），要考虑减少变量的个数，最终所使用变量的个数可根据如下条件判断：‎ ‎（1）直线（一维）上的点：用一个变量就可以表示出所求点的坐标 ‎（2）平面（二维）上的点：用两个变量可以表示所求点坐标 规律：维度=所用变量个数 ‎3、如何减少变量：‎ ‎（1）直线上的点（重点）：平面向量共线定理——若使得 ‎ 例：已知，那么直线上的某点坐标可用一个变量表示，方法如下：——三点中取两点构成两个向量 因为在上，所以 ——共线定理的应用（关键）‎ ‎，即——仅用一个变量表示 ‎（2）平面上的点：平面向量基本定理——若不共线，则平面上任意一个向量，均存在，使得： ‎ 例：已知，则平面上的某点 坐标可用两个变量表示，方法如下：，故，即 二、典型例题 例1：（2010 天津）在长方体中，分别是棱上的点，，‎ ‎（1）求异面直线所成角的余弦值 ‎（2）证明：平面 ‎（3）求二面角正弦值 解：由长方体得：两两垂直 ‎ 以为轴建立空间直角坐标系 ‎（1） ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎（2），设平面的法向量为 ‎ ‎ ‎ ‎ ‎ ‎ 平面 ‎（3）设平面的法向量 ‎ ‎ ‎ ‎ ‎ 例2：如图，在四棱锥中，底面是矩形，平面，，，若分别为棱上的点，为中点，且 ‎ ‎（1）求证：平面平面 ‎ ‎（2）求直线与平面所成角的正弦值 ‎（3）求点到平面的距离 解：平面 ‎ ‎ 矩形 ‎ 故两两垂直 以为轴建立空间直角坐标系 ‎ ‎ ‎，且分别为的中线 ‎ ‎ 设点，因为三点共线 ‎ 而 ‎ ‎ ‎ ‎ 而 ‎ ‎ ‎ ‎ 同理，设点，因为三点共线 ‎ 而 ‎ ‎ ‎ ‎ 而 ‎ ‎ ‎ ‎ ‎（1）设平面的法向量为 ‎ ‎ ‎ 设平面的法向量为 ‎ ‎ ‎ ‎ ‎ ‎ 平面平面 ‎（2）设平面的法向量为 ‎ ‎ ‎ ‎ ‎ 而 ‎ 设直线与平面所成角为，则 ‎（3） ‎ 例3：已知在四棱锥中，底面是矩形，且平面 ，分别是线段的中点 ‎（1）求证： ‎ ‎（2）在线段上是否存在点，使得平面，若存在，确定点的位置；若不存在，请说明理由 ‎（3）若与平面所成的角为，求二面角的余弦值 解：因为平面，且四边形是矩形 ‎ 以为轴建立空间直角坐标系，设 ‎ ‎ ‎ ‎（1） ‎ ‎ ‎ ‎（2）设 ‎ 设平面的法向量为 ‎ ‎ ‎ 平面 ‎ 解得 ‎ ‎ 存在点，为的四等分点（靠近）‎ ‎（3）底面 在底面的投影为 ‎ 为与平面所成的角，即 为等腰直角三角形 即 ‎ 平面的法向量为 平面为平面，所以平面的法向量为 ‎ 设二面角的平面角为，可知为锐角 ‎ ‎ 例4：四棱锥中，平面平面，是中点 ‎（1）求证：平面 ‎（2）求二面角的平面角的余弦值 ‎（3）在侧棱上是否存在点，使得平面，若存在，求出的值；若不存在，请说明理由 解：过在平面作的垂线交于 为中点 ‎ 平面平面 平面 以为轴建立空间直角坐标系 ‎（1） 设平面的法向量为 ‎ ‎ ‎ 平面 ‎（2）设平面的法向量为 ‎ ‎ 设平面的法向量为 ‎ ‎ 所以二面角的平面角的余弦值为 ‎（3）设 ‎ ‎ 而平面的法向量为 平面 ‎ ‎ ‎ 例5：已知四棱锥中，平面，底面是边长为的菱形，，‎ ‎（1）求证：平面平面 ‎ ‎（2）设与交于点，为中点，若二面角 的正切值是，求的值 建系思路一：由与底面垂直，从而以作为轴，以为轴，由的菱形性质可得取中点，连结则有，从而建立空间直角坐标系 解：取中点，连结，可得 ‎ 平面 ‎ 以为轴建立空间直角坐标系 ‎ 可得： ‎ ‎（1）设平面的法向量为 ‎ ‎ ‎ 设平面的法向量为 ‎ ‎ ‎ ‎ 平面平面 ‎（2）‎ 设平面的法向量为 ‎ ‎ ‎ 设平面的法向量为 ‎ ‎ 设二面角的平面角为，则，可得 ‎ ‎ ‎ ‎ ‎ 建系思路二：由思路一可发现尽管建系思路简单，但是所涉及的点的坐标过于复杂，而导致后面的计算繁杂。所以考虑结合图形特点，建立坐标简单的坐标系，从而简化运算：利用菱形对角线垂直的特点，以为坐标原点。过作的平行线，即可垂直底面，从而所建立的坐标系使得底面上的点均在轴上；另一方面，可考虑以为单位长度，可得，避免了坐标中出现过多的字母 解：过作，平面 平面 因为为菱形，所以 ‎ 以为轴建立空间直角坐标系，以为单位长度 ‎ ‎ ‎（1）设平面的法向量为 ‎ ‎ ‎ 设平面的法向量为 因为平面即为平面 ‎ ‎ ‎ 平面平面 ‎（2）‎ 设平面的法向量为 ‎ ‎ ‎ 设平面的法向量为 ‎ ‎ 设二面角的平面角为，则，可得 ‎ ‎ ‎ ‎ ‎ 例6：如图，在边长为4的菱形中，于点，将沿折起到的位置，使得 ‎（1）求证：平面 ‎ ‎（2）求二面角的余弦值 ‎（3）判断在线段上是否存在一点，使平面平面，若存在，求出的值，若不存在，请说明理由 解：（1） ‎ ‎ 平面 ‎ ‎ ‎ ‎ 平面 ‎ ‎（2） ‎ ‎ 两两垂直 以为坐标轴建立坐标系 计算可得： ‎ ‎ ‎ ‎（2）平面的法向量为 ‎ 设平面的法向量为 ‎ ‎ ‎ ‎ ‎ ‎ ‎ 设二面角的平面角为 ‎ ‎ ‎ ‎（3）设 ‎ 设平面的法向量为 ‎ ‎ ‎ ‎ ‎ ‎ ‎ 平面平面 ‎ 解得： ‎ 不在线段上，故不存在该点 小炼有话说：（1）对待翻折问题要注意在翻折的过程中，哪些量和位置关系是不变的，要将平面图形的相关量与翻折后的几何体建立对应关系。‎ ‎（2）在处理点的存在性问题时，求该点所在平面法向量的过程中会遇到所解方程含参的情况，此时可先从含参方程入手，算出满足方程的一组值，再代入另一方程计算会比较简便。‎ 例7：如图，在四棱锥中，底面是平行四边形，平面，点分别为的中点，且．‎ ‎（1）证明：∥平面； ‎ ‎（2）设直线与平面所成角为，当在内变化时，求二面角的取值范围．‎ 解： ‎ 平面 ‎ 以为轴建立直角坐标系，设 ‎（1），设平面的法向量为 ‎ ‎ ‎∥平面 ‎（2）设平面的法向量为 ‎ ‎ ‎ ‎ ‎ 即 平面的法向量为 ‎ 由可得 ‎ 设二面角的平面角为 则 ‎ 例8：在如图所示的多面体中，平面平面，，且，是中点 ‎（1）求证： ‎ ‎（2）求平面与平面所成的锐二面角的余弦值 ‎（3）在棱上是否存在一点，使得直线与平面所成的角为？若存在，指出点的位置，若不存在，请说明理由 解：过在平面上作的平行线 ‎ ‎ 平面 ‎ 两两垂直 如图建系：‎ ‎ ‎ ‎（1） ‎ ‎ ‎ ‎ ‎ ‎（2）设平面的法向量为 ‎ ‎ ‎ 设平面的法向量为 ‎ ‎ 设平面与平面所成的锐二面角的余弦值为 ‎ 则 ‎ ‎（3）设 在上 ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ 解得： ‎ ‎ 存在点，当为中点时，直线与平面所成的角为 例9：如图，在四棱锥中，底面，，，，，点为棱的中点． ‎ ‎（1）证明： ‎ ‎（2）求直线与平面所成角的正弦值 ‎（3）若为棱上一点，满足，求二面角的余弦值 解：底面 ‎ ‎ ‎ 两两垂直，如图建系：‎ ‎ ‎ ‎（1） ‎ ‎ ‎ ‎ ‎ ‎（2）设平面的法向量为 ‎ ‎ ‎ ‎ ‎ 设直线与平面所成角为 ‎ ‎ ‎ ‎（3）设 ‎ 三点共线 ‎ ‎ ‎ ‎ ‎ ‎ 解得： ‎ ‎ ‎ 设平面的法向量为 ‎ ‎ ‎ ‎ ‎ 平面的法向量为 ‎ ‎ ‎ 二面角的余弦值为 例10：如图，在三棱柱，是正方形的中心，，平面，且 ‎（1）求异面直线与所成角的余弦值 ‎（2）求二面角的正弦值 ‎（3）设为棱的中点，点在平面内，且平面，求线段的长 解：连结，因为是正方形的中心 交于，且 平面 如图建系：‎ 设 ‎ ‎ ‎ ‎（1）‎ ‎（2）设平面的法向量为 ‎ ‎ 设平面的法向量为 ‎ ‎ 设二面角的平面角为，则 ‎（3），因为在底面上，所以设 平面的法向量为 平面 ∥‎ ‎，可解得：‎ ‎ ‎ 三、历年好题精选 ‎1、如图，在四棱锥中，底面是直角梯形，侧棱底面，垂直于和，是棱的中点.‎ ‎（1）求证：∥平面 ‎（2）求平面与平面所成的二面角的余弦值 ‎（3）设点是直线上的动点，与平面所成的角为，求的最大值 ‎2、（2015，北京）如图，在四棱锥中，为等边三角形，平面平面，∥为的中点 ‎（1）求证： ‎ ‎（2）求二面角的余弦值 ‎（3）若平面，求的值 T F D E A G B H C ‎3、（2015，山东）如图，在三棱台中，分别为的中点.‎ ‎（1）求证：平面；‎ ‎（2）若平面,求平面与平面所成角（锐角）的大小.‎ ‎4、（北京）如图，正方形的边长为2，分别为的中点，在五棱锥中，为棱的中点，平面与棱分别交于点 ‎（1）求证：‎ ‎（2）若底面，且，求直线与平面所成角的大小，并求线段的长 ‎5、（江西）如图，四棱锥中，为矩形，平面平面 ‎（1）求证：‎ ‎（2）若，问为何值时，四棱锥的体积最大？并求此时平面与平面夹角的余弦值 习题答案：‎ ‎1、解析：（1）以点为坐标原点，如图建系：‎ 则 设平面的法向量为 ‎，可得：‎ ‎ ‎ ‎∥平面 ‎（2）可知平面的法向量为，‎ 设平面与平面所成的二面角为，可得 所成的二面角余弦值为 ‎（3）设，则，平面的法向量为 当即时，取得最大值，即 ‎2、解析：（1） 为等边三角形且为的中点 ‎ ‎ 平面平面 平面 ‎（2）取中点，连结，分别以为轴如图建系 可得： ‎ 设平面的法向量为 ‎ 由可得：‎ ‎ ，可得： ‎ 平面的法向量 ‎ ‎ 由二面角为钝二面角可知 ‎ ‎（3），设平面的法向量为 ‎ ‎ ‎ ‎ 解得 ‎ 平面 ，因为 ‎ ‎，解得：（舍）， ‎ ‎3、解析：（1）证明：连结，设交于点 ‎ 在三棱台中，由可得 ‎ 为中点 ‎，即且 四边形是平行四边形 为中点且 z x y F D E A G B H C 在中，可得为中位线 ‎ 又平面，平面，故平面；‎ ‎（2）由平面,可得平面而 则,于是两两垂直，‎ 以点G为坐标原点，所在的直线 分别为轴建立空间直角坐标系，‎ 设,则,‎ ‎，‎ 则平面的一个法向量为，‎ 设平面的法向量为，则,即，‎ 取，则，，‎ ‎，故平面与平面所成角（锐角）的大小为.‎ ‎4、解析：（1）证明：在正方形中，可知 平面 平面 平面，且平面平面 ‎（2）因为底面，所以 如图建立空间直角坐标系，则 设平面的法向量为 ‎ ‎ 解得 ‎ ‎ 设直线与平面所成角为，则 ‎ 设点，由在棱上可得：‎ 由为平面的法向量可得：‎ 解得 ‎ ‎ ‎5、解析：（1）证明：因为为矩形，所以 又平面平面，且平面平面 平面 ‎（2）过作的垂线，垂足为，过作的垂线 垂足为，连结 平面，平面 在中，‎ 设，则 ‎ ，当时，最大 此时 如图建系，可得：‎ 设平面的一个法向量为 则解得 设平面的一个法向量为 则解得 设平面与平面夹角为，可得