2020届二轮复习正弦函数、余弦函数的性质第2课时课件（38张）（全国通用） 38页

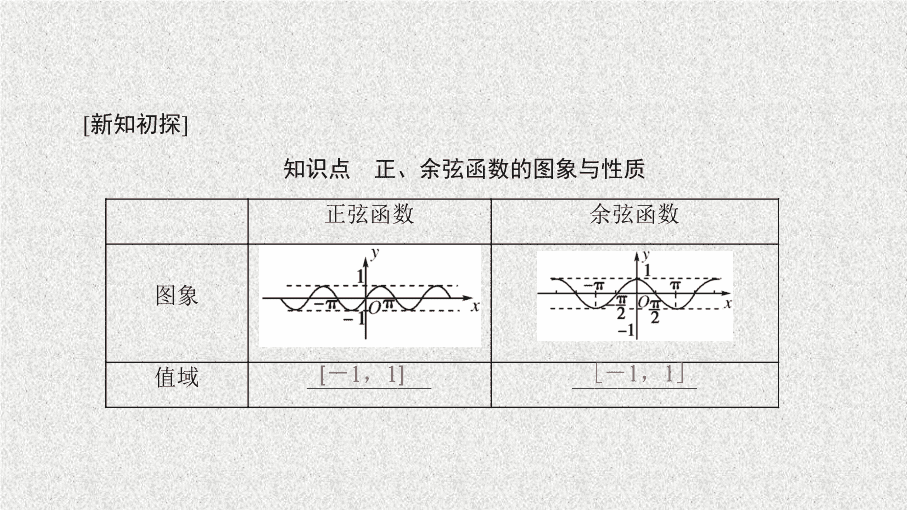
抓基础 · 新知探究 [ － 1 ， 1 ] [ － 1 ， 1 ] [ 2 k π － π ， 2 k π ] [ 2 k π ， 2 k π ＋ π ] 2 k π 2 k π ＋ π 答案：　 B 答案：　 B 答案：　 B 答案：　 > 通技法 · 互动讲练 [ 思想方法 ] 三角函数相关的恒成立问题 ◎ 若 cos 2 θ ＋ 2 m sin θ － 2 m － 2 ＜ 0 恒成立，求实数 m 的取值范围 . 【 分析 】 　本题主要考查三角函数的性质与一元二次不等式的知识 ， 可将原不等式化为 sin 2 θ － 2 m sin θ ＋ 2 m ＋ 1 ＞ 0 ， 令 sin θ ＝ t ， 由于－ 1 ≤ sin θ ≤ 1 ， 故－ 1 ≤ t ≤ 1 ， 只要求出使函数 f ( t ) ＝ t 2 － 2 mt ＋ 2 m ＋ 1( － 1 ≤ t ≤ 1) 的最小值大于 0 的 m 的取值范围即可 . 提知能 · 高效测评 谢谢观看！