2018届二轮复习第二讲三角恒等变换与解三角形教案 8页

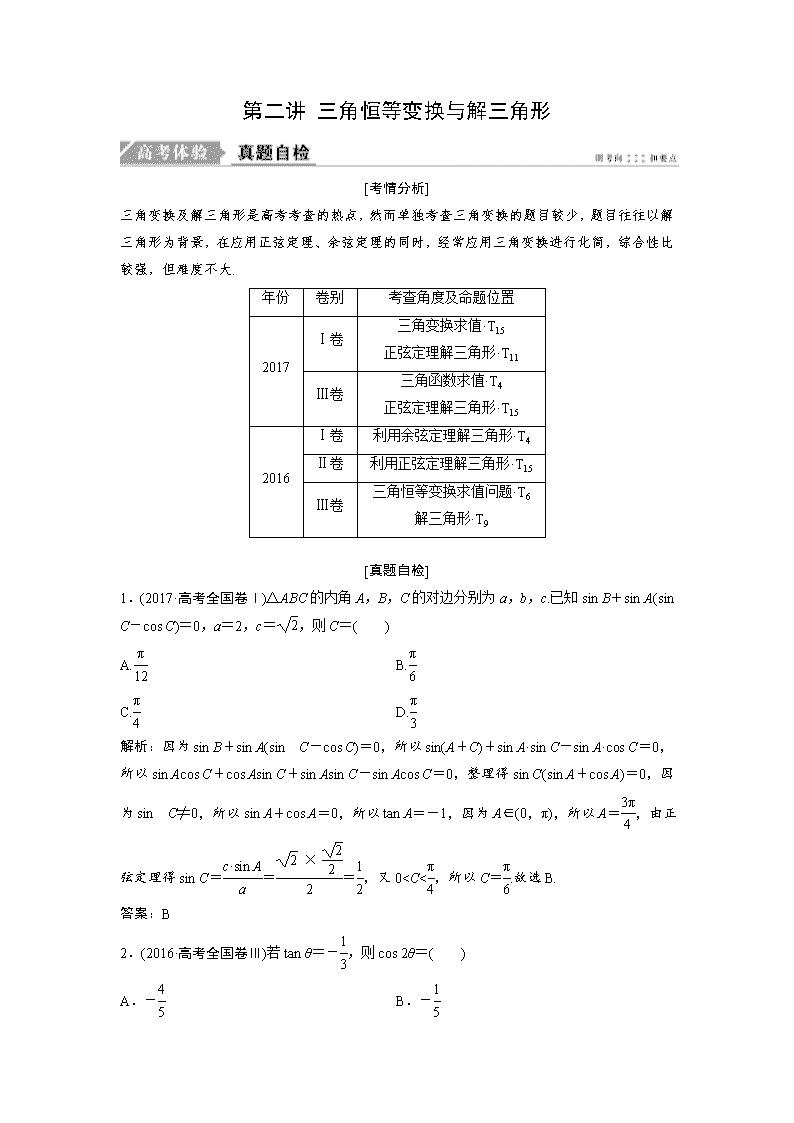
第二讲 三角恒等变换与解三角形 ‎[考情分析]‎ 三角变换及解三角形是高考考查的热点，然而单独考查三角变换的题目较少，题目往往以解三角形为背景，在应用正弦定理、余弦定理的同时，经常应用三角变换进行化简，综合性比较强，但难度不大.‎ 年份 卷别 考查角度及命题位置 ‎2017‎ Ⅰ卷 三角变换求值·T15‎ 正弦定理解三角形·T11‎ Ⅲ卷 三角函数求值·T4‎ 正弦定理解三角形·T15‎ ‎2016‎ Ⅰ卷 利用余弦定理解三角形·T4‎ Ⅱ卷 利用正弦定理解三角形·T15‎ Ⅲ卷 三角恒等变换求值问题·T6‎ 解三角形·T9‎ ‎[真题自检]‎ ‎1．(2017·高考全国卷Ⅰ)△ABC的内角A，B，C的对边分别为a，b，c.已知sin B＋sin A(sin C－cos C)＝0，a＝2，c＝，则C＝(　　)‎ A. B. C. D. 解析：因为sin B＋sin A(sin C－cos C)＝0，所以sin(A＋C)＋sin A·sin C－sin A·cos C＝0，‎ 所以sin Acos C＋cos Asin C＋sin Asin C－sin Acos C＝0，整理得sin C(sin A＋cos A)＝0，因为sin C≠0，所以sin A＋cos A＝0，所以tan A＝－1，因为A∈(0，π)，所以A＝，由正弦定理得sin C＝＝＝，又0