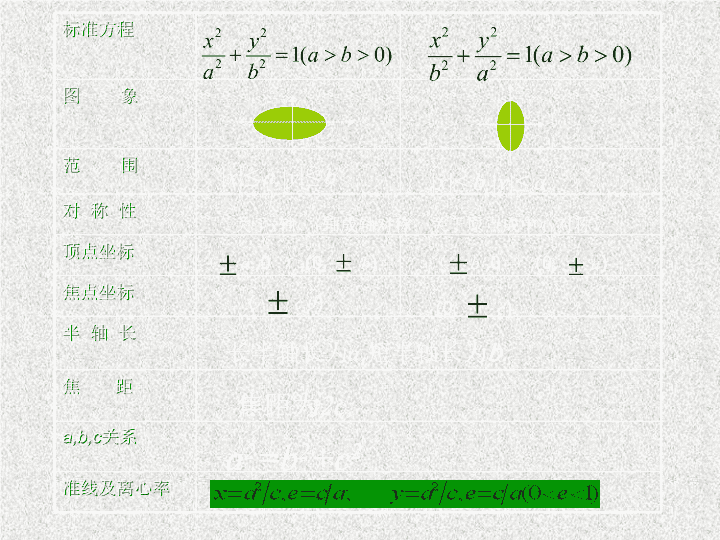- 440.50 KB
- 2021-05-22 发布
课题:椭圆的定义及几何性质
1.
椭圆的定义
(1)
椭圆的第一定义为:平面内与两个定点
F
1
、
F
2
的距离
之和为常数
(
大于
|F
1
F
2
|
)
的点的轨迹叫做椭圆
(2)
椭圆的第二定义为:平面内到一定点
F
与到一定直线
l
的距离之比为一常数
e
(0
<
e
<
1)
的点的轨迹叫做椭圆
一、基础知识复习
2.
椭圆的几何性质
标准方程
图 象
范 围
对 称 性
顶点坐标
焦点坐标
半 轴 长
焦 距
a,b,c
关系
准线及离心率
|x|≤ a,|y|≤ b
|x|≤ b,|y|≤ a
关于
x
轴、
y
轴成轴对称;关于原点成中心对称。
(
a
,0
)
,(0,
b
)
(
b
,0
)
,(0,
a
)
(
c,0
)
(0,
c
)
长半轴长为
a
,
短半轴长为
b.
焦距为
2c;
a
2
=b
2
+c
2
焦半径:
弦长公式:
|PF
1
|= a+ex |PF
2
|= a-ex
|AB|=√1+k
2
|x
1
-x
2
|
= √1+(1/k)
2
|y
1
-y
2
|
F
1
F
2
P
X
Y
o
补充:
二、基础练习
1.
椭圆
x
2
/100+
y
2
/64=1
上一点
P
到左焦点
F
1
的距离为
6
,
Q
是
PF
1
的中点,
O
是坐标原点,则
|OQ|=
_____
7
2.
已知椭圆上横坐标等于焦点横坐标的点,其纵坐标等于
短半轴长的
2/3
,则椭圆的离心率为
_______
3.
已知方程
表示焦点
y
轴上的椭圆,则
m
的
取值范围是
( )
(A)
m
<
2
(B)
1
<
m
<
2
(C)
m
<
-1
或
1
<
m
<
2
(D)
m
<
-1
或
1
<
m
<
3
/
2
D
4.
已知动点
P
、
Q
在椭圆
9
x
2
+16
y
2
=144
上
.
椭圆的中心为
O
,且
OP
·
OQ
=0
,则中心
O
到弦
PQ
的距离
OH
必等于
( )
(A) (B) (C) (D)
→
→
返回
C
5.
已知
F
1
、
F
2
是椭圆
x
2
/25
+y
2
/9=1
的焦点,
P
为椭圆上一点
.
若∠
F
1
PF
2
=60°.
则△
PF
1
F
2
的面积是
________.
三、例题讲解
:
【
解题回顾
】
本题因椭圆焦点位置未定,故有两种情况,不能犯
“
对而不全
”
的知识性错误
【
例
1】
已知
P
点在以坐标轴为对称轴的椭圆上,点
P
到
两焦点的距离分别为 和 ,过
P
作长轴的垂线恰好
过椭圆的一个焦点,求椭圆方程
【
解题回顾
】
求椭圆的方程,先判
断焦点的位置,若焦点位置不确定
则进行讨论,还要善于利用椭圆的
定义和性质结合图形建立关系式
2.
如图,从椭圆
x
2
/
a
2
+y
2
/
b
2
=1(
a
>
b
>
0)
上一点
P
向
x
轴作垂线,垂足恰为左焦点
F
1
,
A
是椭圆与
x
轴正半轴的交点,
B
是椭圆与
y
轴正半轴的交点,且
AB
∥
OP
,
|F
1
A|
=√10+√5
,求此椭圆方程
【
解题回顾
】
|AF
2
|
与
|BF
2
|
为焦半
径,所以考虑使用焦半径公式建
立关系式,同时结合图形,利用
平面几何知识在应用椭圆第二
定义时,必须注意相应的焦点和准线问题
3.
已知
A
、
B
是椭圆
上的点,
F
2
是右焦点且
|AF
2
|+|BF
2
|=
,
AB
的中点
N
到左准线的距离等于 ,求此
椭圆方程
四、课堂回顾
:
1
、椭圆的定义:
第一定义是什么?
第二定义又是什么?
2
、椭圆几何性质:
长轴、短轴、顶点、焦点、对称轴、
对称中心、准线、离心率、焦半径。