反比例函数的图象及其性质同步练习3 2页

9.2 反比例函数的图象及其性质（3） 同步练习 【目标与方法】 1．巩固反比例函数的图象性质，并能运用其与对应的函数关系式之间的内在联系及其几 何意义解决有关问题． 2．根据所给反比例函数与一次函数的图象解决一些简单的综合问题． 【基础与巩固】 1．反比例函数 y= 1m x  的图象在第二、四象限，则 m 的取值范围是________． 2．已知反比例函数 y= k x 与一次函数 y=2x+k 的图象的一个交点的横坐标是-4，则 k 的值 是__________． 3．已知点（x1，-1），（x2，- 5 2 ），（x3，2）在函数 y=- 1 x 的图象上，则下列关系式正确的 是（ ）． （A）x1>x2>x3（B）x3>x2>x1（C）x2>x1>x3（D）x3>x1>x2 4．已知反比例函数 y= 5 m x  的图象在每一个象限内，y 随 x 增大而增大，则（ ）． （A）m≥5 （B）m<5 （C）m>5 （D）m≤5 5．点 A（-2，a），B（-1，b），C（3，c）在双曲线 y= k x （k>0）上，试确定 a，b，c 的大 小关系． 6．如图，已知反比例函数 y= k x 的图象经过点 A（- 3 ，b），过点 A 作 x 轴的垂线，垂足 为点 B，△AOB 的面积为 3 ，求 k 和 b 的值． 【拓展与延伸】 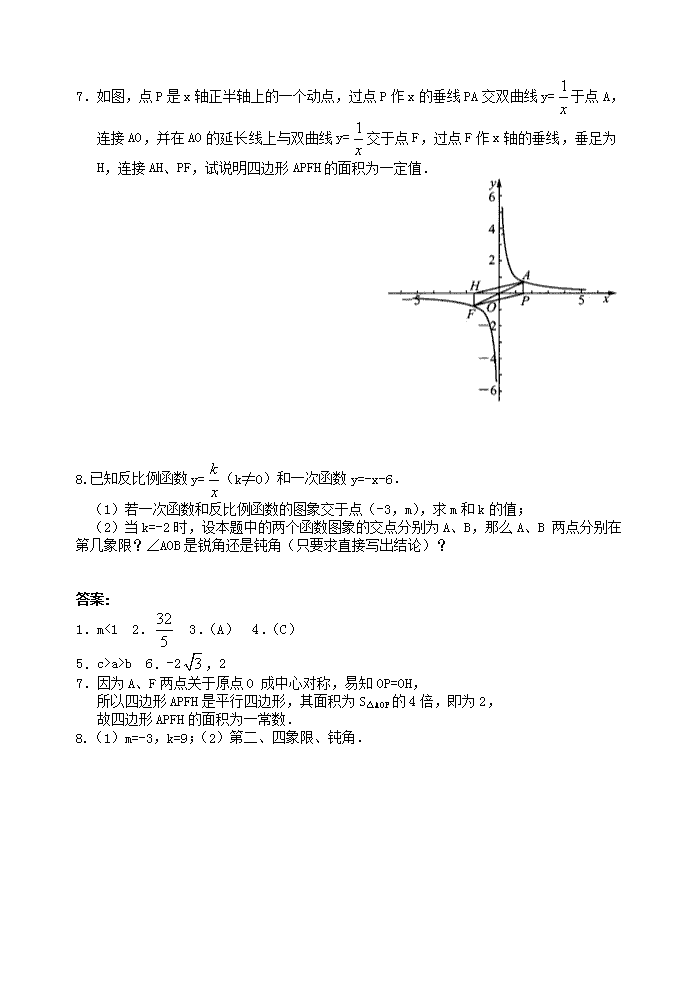7．如图，点 P 是 x 轴正半轴上的一个动点，过点 P 作 x 的垂线 PA 交双曲线 y= 1 x 于点 A， 连接 AO，并在 AO 的延长线上与双曲线 y= 1 x 交于点 F，过点 F 作 x 轴的垂线，垂足为 H， 连接 AH、PF，试说明四边形 APFH 的面积为一定值． 8.已知反比例函数 y= k x （k≠0）和一次函数 y=-x-6． （1）若一次函数和反比例函数的图象交于点（-3，m），求 m 和 k 的值； （2）当 k=-2 时，设本题中的两个函数图象的交点分别为 A、B，那么 A、B两点分别在 第几象限？∠AOB 是锐角还是钝角（只要求直接写出结论）？ 答案: 1．m<1 2． 32 5 3．（A） 4．（C） 5．c>a>b 6．-2 3 ，2 7．因为 A、F 两点关于原点 O成中心对称，易知 OP=OH， 所以四边形 APFH 是平行四边形，其面积为 S△AOP 的 4 倍，即为 2， 故四边形 APFH 的面积为一常数． 8.（1）m=-3，k=9；（2）第二、四象限、钝角．