2021高考数学一轮复习专练35二元一次不等式组与简单的线性规划问题含解析理新人教版 6页

专练35　二元一次不等式(组)与简单的线性规划问题 命题范围：二元一次不等式(组)简单的线性规划问题 ‎[基础强化]‎ 一、选择题 ‎1．在3x＋2y＜6表示的平面区域内的一个点是(　　)‎ A．(3,0)　　　　　　　　　B．(1,3)‎ C．(0,3) D．(0,0)‎ ‎2．不等式组所表示的平面区域的面积等于(　　)‎ A．3 B．9‎ C．18 D．36‎ ‎3．设P(x，y)其中x，y∈N，满足x＋y≤3的点P的个数为(　　)‎ A．10 B．9‎ C．3 D．无数个 ‎4．已知点P(1，－2)，Q(a,2)，若直线2x＋y－4＝0与线段PQ有公共点，则实数a的取值范围是(　　)‎ A．[1，＋∞) B．(1，＋∞)‎ C．(－∞，1] D．(－∞，1)‎ ‎5．[2019·天津卷]设变量x，y满足约束条件则目标函数z＝－4x＋y的最大值为(　　)‎ A．2 B．3‎ C．5 D．6‎ ‎6．[2020·贵阳一中高三测试]若以不等式组的解为坐标的点所表示的平面区域为三角形，且其面积为，则实数a的值可以为(　　)‎ A．－3 B．1‎ C．－3或1 D．3或－1‎ ‎7．[2019·浙江卷]若实数x，y满足约束条件则z＝3x＋2y的最大值是(　　)‎ A．－1 B．1‎ C．10 D．12‎ ‎8．[2020·石家庄一中高三测试]若变量x，y满足则x2＋y2的最大值是(　　)‎ A．4 B．9‎ C．10 D．12‎ ‎9．[2020·银川一中高三测试]若x，y满足约束条件则t＝的范围是(　　)‎ A. B. C. D. 二、填空题 ‎10．[2020·全国卷Ⅲ]若x，y满足约束条件则z＝3x＋2y的最大值为________．‎ ‎11．若x，y满足约束条件则z＝x＋y的最大值为________．‎ ‎12．[2020·邯郸一中高三测试]已知实数x，y满足则的取值范围为________．‎ ‎[能力提升]‎ ‎13．若z＝mx＋y在平面区域上取得最小值时的最优解有无穷多个，则z的最小值是(　　)‎ A．－1 B．1‎ C．0 D．0或±1‎ ‎14．[2020·开封一中高三测试]已知x，y满足条件则目标函数z＝x＋y从最小值变化到1时，所有满足条件的点(x，y)构成的平面区域的面积为(　　)‎ A. B. C. D. ‎15．[2020·全国卷Ⅰ]若x，y满足约束条件则z＝x＋7y的最大值为________．‎ ‎16．[2020·合肥一中高三测试]已知实数x，y满足存在x，y使得2x＋y≤a成立，则实数a的取值范围是________．‎ 专练35　二元一次不等式(组)与简单的线性规划问题 ‎1.D ‎2.‎ C　在平面直角坐标系中画出可行域如图的阴影部分所示，该阴影部分的形状为等腰梯形，其面积S＝×(3＋9)×3＝18.‎ ‎ 解析图3.A　当x＝0时，y＝0,1,2,3，共4个点；‎ 当x＝1时，y＝0,1,2，共3个点；‎ 当x＝2时，y＝0,1，共2个点；‎ 当x＝3时，y＝0，共1个点．‎ ‎∴共有4＋3＋2＋1＝10个点．‎ ‎4．A　直线2x＋y－4＝0与线段PQ有公共点，说明点P，Q不在直线2x＋y－4＝0的同一侧，∴(2－2－4)(‎2a＋2－4)≤0，解得a≥1，实数a的取值范围是[1，＋∞)，故选A.‎ ‎5．C　本题主要考查线性规划，考查数形结合思想，考查的核心素养是数学运算、直观想象．‎ 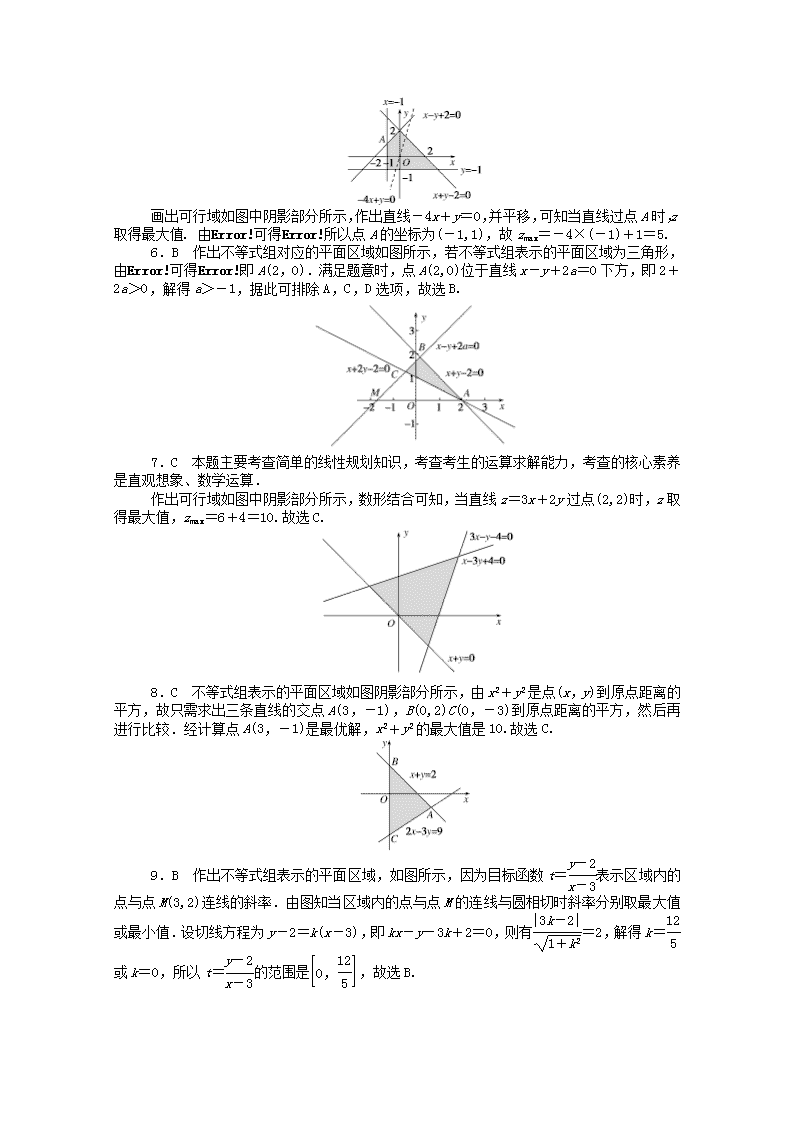画出可行域如图中阴影部分所示，作出直线－4x＋y＝0，并平移，可知当直线过点A时，z取得最大值. 由可得所以点A的坐标为(－1,1)，故zmax＝－4×(－1)＋1＝5.‎ ‎6．B　作出不等式组对应的平面区域如图所示，若不等式组表示的平面区域为三角形，由可得即A(2，0)．满足题意时，点A(2,0)位于直线x－y＋‎2a＝0下方，即2＋‎2a＞0，解得a＞－1，据此可排除A，C，D选项，故选B.‎ ‎7．C　本题主要考查简单的线性规划知识，考查考生的运算求解能力，考查的核心素养是直观想象、数学运算．‎ 作出可行域如图中阴影部分所示，数形结合可知，当直线z＝3x＋2y过点(2,2)时，z取得最大值，zmax＝6＋4＝10.故选C.‎ ‎8．C　不等式组表示的平面区域如图阴影部分所示，由x2＋y2是点(x，y)到原点距离的平方，故只需求出三条直线的交点A(3，－1)，B(0,2)C(0，－3)到原点距离的平方，然后再进行比较．经计算点A(3，－1)是最优解，x2＋y2的最大值是10.故选C.‎ ‎9．B　作出不等式组表示的平面区域，如图所示，因为目标函数t＝表示区域内的点与点M(3,2)连线的斜率．由图知当区域内的点与点M的连线与圆相切时斜率分别取最大值或最小值．设切线方程为y－2＝k(x－3)，即kx－y－3k＋2＝0，则有＝2，解得k＝或k＝0，所以t＝的范围是，故选B.‎ ‎10．7‎ 解析：如图所示，x，y满足的可行域为△AOB及其内部．‎ 由目标函数z＝3x＋2y得y＝－x＋.‎ 当直线y＝－x＋过点A(1,2)时，z取最大值，最大值为7.‎ ‎11．9‎ 解析：不等式组表示的平面区域如图中阴影部分所示．‎ 由图可得直线x＋y＝z过点C时z取得最大值．‎ 由得点C(5,4)，‎ ‎∴ zmax＝5＋4＝9.‎ ‎12. 解析：不等式组表示的平面区域如图所示，目标函数表示点D(－3，－1)与可行域内的点连线的斜率，很明显，在坐标原点处，目标函数取得最小值＝，联立方程得可得则在点B处取得最大值＝，综上可得，的取值范围为.‎ ‎13．C　画出平面区域如图所示，可以判断出z的几何意义是直线mx＋y－z＝0在y轴上的截距，只有直线mx＋y－z＝0与直线x－2y＝0重合时，才符合题意，此时，相应z的最小值为0.‎ ‎14．A　画出表示的可行域，如图，平移直线y＝－x＋z，从经过点A到与直线BC：y＝－x＋1重合，目标函数z＝x＋y从最小值连续变化到1，满足条件的点(x，y)构成的平面区域的面积为四边形ABCO，面积为×2×2－×1×＝，故选A.‎ ‎15．1‎ 解析：作出可行域如图，由z＝x＋7y得y＝－＋，易知当直线y＝－＋经过点A(1,0)时，z取得最大值，zmax＝1＋7×0＝1.‎ ‎16．[2，＋∞)‎ 解析：令z＝2x＋y，画出约束条件的可行域，由可行域知目标函数过点B时取最小值，由可得x＝－1，y＝4，可得B(－1,4)，z的最小值为2×(－1)＋4＝2.所以若存在x，y，使2x＋y≤a成立，只需使a≥(2x＋y)min，所以a≥2.‎