2018届二轮复习考前教材重温学案（全国通用） 26页

专题一　考前教材重温 ‎1. ‎1．α终边与θ终边相同(α的终边在θ终边所在的射线上)⇔α＝θ＋2kπ(k∈Z)，注意：相等的角的终边一定相同，终边相同的角不一定相等．‎ 任意角的三角函数的定义：设α是任意一个角，P(x，y)是α的终边上的任意一点(异于原点)，它与原点的距离是r＝>0，那么sin α＝，cos α＝，tan α＝(x≠0)，三角函数值只与角的大小有关，而与终边上点P的位置无关．‎ ‎[应用1]　已知角α的终边经过点P(3，－4)，则sin α＋cos α的值为________．‎ ‎[答案]　－ ‎2．同角三角函数的基本关系式及诱导公式．‎ ‎(1)平方关系：sin2α＋cos2α＝1.‎ ‎(2)商数关系：tan α＝.‎ ‎(3)诱导公式记忆口诀：奇变偶不变、符号看象限．‎ 角 ‎－α π－α π＋α ‎2π－α －α 正弦 ‎－sin α sin α ‎－sin α ‎－sin α cos α 余弦 cos α ‎－cos α ‎－cos α cos α sin α ‎[应用2]　cos＋tan＋sin 21π的值为________．‎ ‎[答案]　－ ‎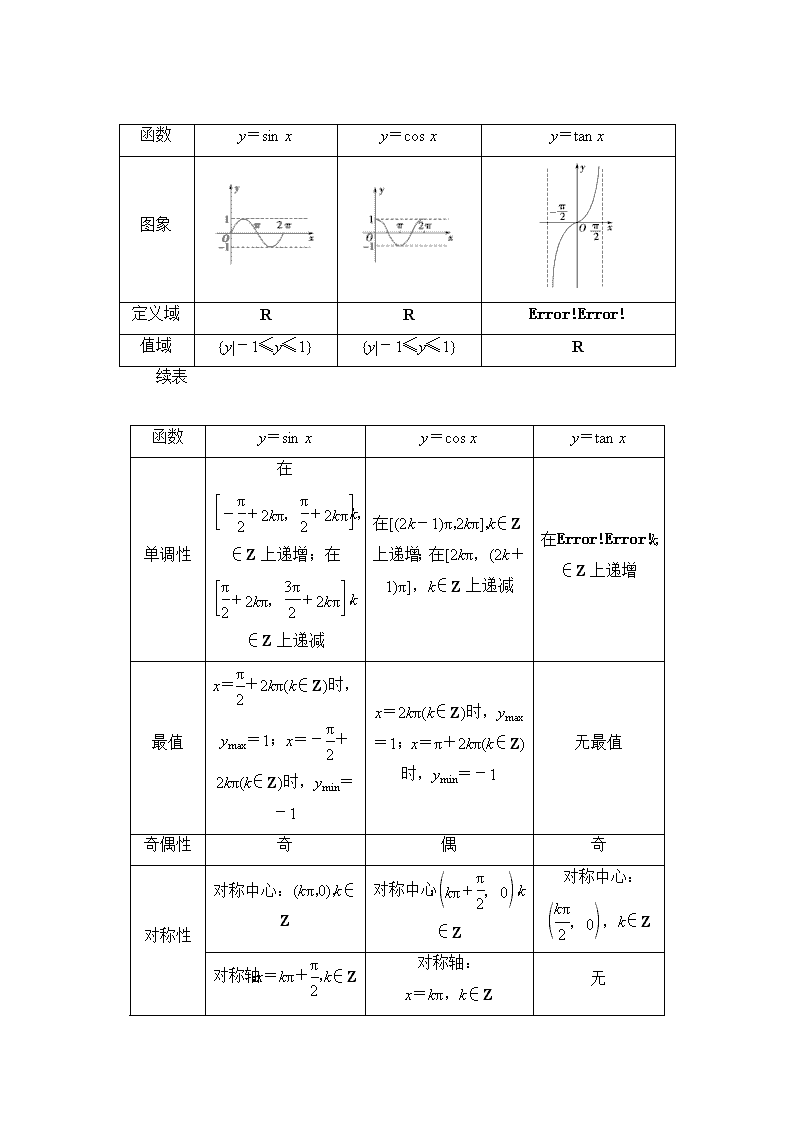3．正弦、余弦和正切函数的常用性质．‎ 函数 y＝sin x y＝cos x y＝tan x 图象 定义域 R R 值域 ‎{y|－1≤y≤1}‎ ‎{y|－1≤y≤1}‎ R 续表　　‎ 函数 y＝sin x y＝cos x y＝tan x 单调性 在，k∈Z上递增；在，k∈Z上递减 在[(2k－1)π，2kπ]，k∈Z上递增；在[2kπ，(2k＋1)π]，k∈Z上递减 在，k∈Z上递增 最值 x＝＋2kπ(k∈Z)时，ymax＝1；x＝－＋2kπ(k∈Z)时，ymin＝－1‎ x＝2kπ(k∈Z)时，ymax＝1；x＝π＋2kπ(k∈Z)时，ymin＝－1‎ 无最值 奇偶性 奇 偶 奇 对称性 对称中心：(kπ，0)，k∈Z 对称中心：，k∈Z 对称中心：，k∈Z 对称轴：x＝kπ＋，k∈‎ 对称轴：‎ x＝kπ，k∈Z 无 Z 周期性 ‎2π ‎2π π ‎[应用3]　函数y＝sin的递减区间是________．‎ ‎[答案]　(k∈Z)‎ ‎4．三角函数化简与求值的常用技巧．‎ 解答三角变换类问题要灵活地正用、逆用，变形运用和、差、倍角公式和诱导公式，进行化简、求值．常用到切割化弦、降幂、拆角拼角等技巧．如：‎ α＝(α＋β)－β，2α＝(α＋β)＋(α－β)，‎ α＝[(α＋β)＋(α－β)]．‎ α＋＝(α＋β)－，α＝－.‎ ‎[应用4]　已知α，β∈，sin(α＋β)＝－，sin＝，则cos＝________.‎ ‎[答案]　－ ‎5．解三角形．‎ ‎(1)正弦定理：＝＝＝2R(R为三角形外接圆的半径)．注意：①正弦定理的一些变式：(i)a∶b∶c＝sin A∶sin B∶sin C；(ⅱ)sin A＝，sin B＝，sin C＝；(ⅲ)a＝2Rsin A，b＝2Rsin B，c＝2Rsin C；②已知三角形两边及一对角，求解三角形时，若运用正弦定理，则务必注意可能有两解，要结合具体情况进行取舍．在△ABC中，A>B⇔sin A＞sin B.‎ ‎(2)余弦定理：a2＝b2＋c2－2bccos A，cos A＝等，常选用余弦定理判定三角形的形状．‎ ‎[应用5]　在△ABC中，a＝，b＝，A＝60°，则B＝________.‎ ‎[答案]　45°‎ ‎6．求三角函数最值的常见类型、方法．‎ ‎(1)y＝asin x＋b(或acos x＋b)型，利用三角函数的值域，须注意对字母a的讨论．‎ ‎(2)y＝asin x＋bsin x型，借助辅助角公式化成y＝sin(x＋φ)的形式，再利用三角函数有界性解决．‎ ‎(3)y＝asin2x＋bsin x＋c型，配方后转化为二次函数求最值，应注意|sin x|≤1的约束．‎ ‎(4)y＝型，反解出sin x，化归为|sin x|≤1解决．‎ ‎(5)y＝型，化归为Asin x＋Bcos x＝C型或用数形结合法(常用到直线斜率的几何意义)求解．‎ ‎(6)y＝a(sin x＋cos x)＋bsin x·cos x＋c型，常令t＝sin x＋cos x，换元后求解(|t|≤)．‎ ‎[应用6]　函数y＝sin2x＋sin x－1的值域为________．‎ ‎[答案]　 ‎7．向量的平行与平面向量的数量积．‎ ‎(1)向量平行(共线)的充要条件：a∥b(b≠0)⇔a＝λb⇔(a·b)2＝(|a||b|)2⇔x1y2－y1x2＝0.‎ ‎(2)a·b＝|a||b|cos θ，‎ 变形：|a|2＝a2＝a·a，cos θ＝，‎ a在b上的投影(正射影的数量)＝.‎ 注意：〈a，b〉为锐角⇔a·b>0且a，b不同向；‎ ‎〈a，b〉为钝角⇔a·b＜0且a，b不反向．‎ ‎[应用7]　已知圆O为△ABC的外接圆，半径为2，若＋＝2，且||＝||，则向量在向量方向上的投影为________．‎ ‎[答案]　3‎ ‎8．向量中常用的结论．‎ ‎(1)＝λ＋μ(λ，μ为实数)，若λ＋μ＝1，则三点A，B，C共线；‎ ‎(2)在△ABC中，若D是BC边的中点，则＝(＋)；‎ ‎(3)已知O，N，P在△ABC所在平面内．若||＝||＝||，则O为△ABC的外心；若＋＋＝0，则N为△ABC的重心；若·＝·＝·，则P为△ABC的垂心．‎ ‎[应用8]　在△ABC中，D是AB的中点，E是AC的中点，CD与BE交于点F，设＝a，＝b，＝xa＋yb，则(x，y)为(　　)‎ A.　　　　　　　 B． C. D. ‎[答案]　C ‎2. ‎1.等差数列及其性质．‎ ‎(1)等差数列的判定：an＋1－an＝d(d为常数)或an＋1－an＝an－an－1(n≥2)．‎ ‎(2)等差数列的性质 ‎①当公差d≠0时，等差数列的通项公式an＝a1＋(n－1)·d＝dn＋a1－d是关于n的一次函数，且斜率为公差d；前n项和Sn＝na1＋d＝n2＋n是关于n的二次函数且常数项为0.‎ ‎②若公差d>0，则为递增等差数列；若公差d<0，则为递减等差数列；若公差d＝0，则为常数列．‎ ‎③当m＋n＝p＋q时，则有am＋an＝ap＋aq，特别地，当m＋n＝2p时，则有am＋an＝2ap.‎ ‎④Sn，S2n－Sn，S3n－S2n成等差数列．‎ ‎[应用1]　已知等差数列{an}的前n项和为Sn，且S10＝12，S20＝17，则S30‎ 为(　　)‎ A．15　　　 B．20 ‎ C.25　　　 D．30‎ ‎[答案]　A ‎2．等比数列及其性质．‎ ‎(1)等比数列的判定：＝q(q为常数，q≠0)或＝(n≥2)．‎ ‎(2)等比数列的性质：‎ 当m＋n＝p＋q时，则有am·an＝ap·aq，特别地，当m＋n＝2p时，则有am·an＝a.‎ ‎[应用2] (1)在等比数列{an}中，a3＋a8＝124，a‎4a7＝－512，公比q是整数，则a10＝________.‎ ‎(2)各项均为正数的等比数列{an}中，若a5·a6＝9，则log‎3a1＋log‎3a2＋…＋log‎3a10＝________.‎ ‎[答案] (1)512　(2)10‎ ‎3．求数列通项的常见类型及方法．‎ ‎(1)已知数列的前几项，求数列的通项公式，可采用归纳、猜想法．‎ ‎(2)如果给出的递推关系式符合等差或等比数列的定义，可直接利用等差或等比数列的公式写出通项公式．‎ ‎(3)若已知数列的递推公式为an＋1＝an＋f(n)，可采用累加法．‎ ‎(4)数列的递推公式为an＋1＝an·f(n)，则采用累乘法．‎ ‎(5)已知Sn与an的关系，利用关系式an＝求an.‎ ‎(6)构造转化法：转化为等差或等比数列求通项公式．‎ ‎[应用3]　已知f(x)是定义在R上不恒为零的函数，对于任意的x，y∈R，都有f(xy)＝xf(y)＋yf(x)成立．数列{an}满足an＝f(2n)(n∈N*)，且a1＝2，则数列{an}的通项公式为an＝________.‎ ‎[答案]　n·2n ‎4．数列求和的方法．‎ ‎(1)公式法：等差数列、等比数列求和公式；‎ ‎(2)分组求和法；‎ ‎(3)倒序相加法；‎ ‎(4)错位相减法；‎ ‎(5)裂项法；‎ 如：＝－；＝.‎ ‎(6)并项法；‎ 数列求和时要明确项数、通项，并注意根据通项的特点选取合适的方法．‎ ‎[应用4]　数列{an}满足an＋an＋1＝(n∈N，n≥1)，若a2＝1，Sn是{an}的前n项和，则S21的值为________．‎ ‎[答案]　 ‎5．如何解含参数的一元二次不等式．‎ 解含有参数的一元二次不等式一般要分类讨论，往往从以下几个方面 考虑：①二次项系数，它决定二次函数的开口方向；②判别式Δ，它决定根的情形，一般分Δ>0、Δ＝0、Δ<0三种情况；③在有根的条件下，要比较两根的大小，也是分大于、等于、小于三种情况．在解一元二次不等式时，一定要画出二次函数的图象，注意数形结合．‎ ‎[应用5]　解关于x的不等式ax2－(a＋1)x＋1＜0(a>0)．‎ ‎________________________________________________________________________________________________________________________________________‎ ‎[解]　原不等式化为 (x－1)＜0.‎ ‎∴当0＜a＜1时，不等式的解集为 ；‎ 当a＞1时，不等式的解集为 ；‎ 当a＝1时，不等式的解集为∅.‎ ‎6．处理二次不等式恒成立的常用方法．‎ ‎(1)结合二次函数的图象和性质用判别式法，当x的取值为全体实数时，一般应用此法．‎ ‎(2)从函数的最值入手考虑，如大于零恒成立可转化最小值大于零．‎ ‎(3)能分离变量的，尽量把参变量和变量分离出 ．‎ ‎(4)数形结合，结合图形进行分析，从整体上把握图形．‎ ‎[应用6]　如果kx2＋2kx－(k＋2)<0恒成立，则实数k的取值范围是 (　　)‎ A．－1≤k≤0 B．－1≤k<0‎ C．－1＜k≤0 D．－10)，则f(x)的周期T＝a；(2)f(x＋a)＝(f(x)≠0)或f(x＋a)＝－f(x)，则f(x)的周期T＝‎2a.‎ ‎[应用7]　设f(x)是定义在R上的周期为3的函数，当x∈[－2,1)时，f(x)＝则f＝________.‎ ‎[答案]　－1‎ ‎8．函数图象的几种常见变换．‎ ‎(1)平移变换：左右平移——“左加右减”(注意是针对x而言)；上下平移——“上加下减”．‎ ‎(2)翻折变换：f(x)→|f(x)|；f(x)→f(|x|)．‎ ‎(3)对称变换：①证明函数图象的对称性，即证图象上任意点关于对称中心(轴)的对称点仍在图象上；‎ ‎②函数y＝f(x)与y＝－f(－x)的图象关于原点成中心对称；‎ ‎③函数y＝f(x)与y＝f(－x)的图象关于直线x＝0(y轴)对称；函数y＝f(x)与函数y＝－f(x)的图象关于直线y＝0(x轴)对称．‎ ‎[应用8]　函数y＝的对称中心是________．‎ ‎[答案]　(1,3)‎ ‎9．如何求方程根的个数或范围．‎ 求f(x)＝g(x)根的个数时，可在同一坐标系中作出函数y＝f(x)和y＝g(x)的图象，看它们交点的个数；求方程根(函数零点)的范围，可利用图象观察或零点存在性定理．‎ ‎[应用9]　函数f(x)＝ln(x＋1)－的零点所在的大致区间是 (　　)‎ A．(0,1)　　 B．(1,2) ‎ C.(2，e)　　 D．(3,4)‎ ‎[答案]　B ‎10．二次函数问题．‎ ‎(1)处理二次函数的问题勿忘数形结合．二次函数在闭区间上必有最值，求最值问题用“两看法”：一看开口方向，二看对称轴与所给区间的相对位置关系．‎ ‎(2)若原题中没有指出是“二次”方程、函数或不等式，要考虑到二次项系数可能为零的情形．‎ ‎[应用10]　若关于x的方程ax2－x＋1＝0至少有一个正根，则a的取值范围为________．‎ ‎[答案]　 ‎11．利用导数研究函数单调性的步骤．‎ ‎(1)确定函数y＝f(x)的定义域．‎ ‎(2)求导数y′＝f′(x)．‎ ‎(3)解方程f′(x)＝0在定义域内的所有实根．‎ ‎(4)将函数y＝f(x)的间断点(即函数无定义点)的横坐标和各个实数根按从小到大的顺序排列起 ，分成若干个小区间．‎ ‎(5)确定f′(x)在各个小区间内的符号，由此确定每个区间的单调性．‎ 特别提醒：(1)多个单调区间不能用“∪”连接；‎ ‎(2)f(x)为减函数时f′(x)≤0恒成立，但要验证f′(x)是否恒等于0.‎ ‎[应用11]　函数f(x)＝ax3－2x2＋x－1在R上是增函数，则a的取值范围是________．‎ ‎[答案]　 ‎12．导数为零的点并不一定是极值点，例如：函数f(x)＝x3，有f′(0)＝0，但x＝0不是极值点．‎ ‎[应用12]　函数f(x)＝x4－x3的极值点是________．‎ ‎[答案]　x＝1‎ ‎13．利用导数解决不等式问题的思想．‎ ‎(1)证明不等式f(x)”的否定是“≤”，“都”的否定是“不都”．‎ ‎[应用7]　命题“∀n∈N*，f(n)∈N*且f(n)≤n”的否定形式是(　　)‎ A．∀n∈N*，f(n)∉N*且f(n)＞n B．∀n∈N*，f(n)∉N*或f(n)＞n C．∃n0∈N*，f(n0)∉N*且f(n0)＞n0‎ D．∃n0∈N*，f(n0)∉N*或f(n0)＞n0‎ ‎[答案]　D ‎8．求参数范围时，要根据条件进行等价转化，注意范围的临界值能否取到，也可与补集思想联合使用．‎ ‎[应用8]　已知命题p：∃x0∈R，ax＋x0＋≤0.若命题p是假命题，则实数a的取值范围是________．‎ ‎[答案]　 ‎8. ‎1．归纳推理和类比推理．‎ 共同点：两种推理的结论都有待于证明．‎ 不同点：归纳推理是由特殊到一般的推理，类比推理是由特殊到特殊的推理．‎ ‎[应用1] (1)若数列{an}是等差数列，bn＝，则数列{bn}也为等差数列．类比这一性质可知，若正项数列{cn}是等比数列，{dn}也是等比数列，则{dn}的表达式应为(　　)‎ A．dn＝ B．dn＝ C．dn＝ D．dn＝ ‎(2)若数列{an}的通项公式为an＝(n∈N*)，记f(n)＝(1－a1)(1－a2)…(1－an)，试通过计算f(1)，f(2)，f(3)的值，推测出f(n)＝________.‎ ‎[答案] (1)D　(2) ‎2．证明方法：综合法由因导果，分析法执果索因．反证法是常用的间接证明方法，利用反证法证明问题时一定要理解结论的含义，正确进行反设．‎ ‎[应用2]　用反证法证明命题“三角形三个内角至少有一个不大于60°”时，应假设________________________________________________________．‎ ‎[答案]　三角形三个内角都大于60°‎ ‎3．复数的概念．‎ 对于复数a＋bi(a，b∈R)，a叫做实部，b叫做虚部；当且仅当b ‎＝0时，复数a＋bi(a，b∈R)是实数a；当b≠0时，复数a＋bi叫做虚数；当a＝0且b≠0时，复数a＋bi叫做纯虚数．‎ ‎[应用3]　若复数z＝lg(m2－m－2)＋i·lg(m2＋‎3m＋3)为实数，则实数m的值为________．‎ ‎[答案]　－2‎ ‎4．复数的运算法则与实数运算法则相同，主要是除法法则的运用，另外复数中的几个常用结论应记熟：‎ ‎(1)(1±i)2＝±2i；(2)＝i；＝－i；(3)i4n＝1；i4n＋1＝i；i4n＋2＝－1；i4n＋3＝－i；i4n＋i4n＋1＋i4n＋2＋i4n＋3＝0；‎ ‎(4)设ω＝－±i，则ω0＝1；ω2＝；ω3＝1；1＋ω＋ω2＝0.‎ ‎[应用4]　已知复数z＝，是z的共轭复数，则||＝________.‎ ‎[答案]　1‎ ‎5．(1)循环结构中几个常用变量：‎ ‎①计数变量：用 记录某个事件发生的次数，如i＝i＋1.‎ ‎②累加变量：用 计算数据之和，如s＝s＋i.‎ ‎③累乘变量：用 计算数据之积，如p＝p×i.‎ ‎(2)处理循环结构的框图问题，关键是理解认清终止循环结构的条件及循环次数．‎ ‎[应用5]　(2016·衡水中 七调改编)执行如图6的程序框图，输出S的值为________．‎ 图6‎ ‎[答案]　2‎